
Fizik ve akışkanlar mekaniğinde, bir sınır tabaka (veya sınır katman), bir yüzey boyunca akan akışkanın oluşturduğu, sınır yüzeyinin hemen yakınındaki ince akışkan tabakasıdır. Akışkanın duvar ile etkileşimi, bir kaymazlık sınır koşuluna (duvarda sıfır hız) neden olur. Akış hızı daha sonra, yüzeyden uzaklaştıkça serbest akım hızına ulaşana kadar monoton bir şekilde artar. Hızı henüz serbest akım hızına dönmemiş olan akışkandan oluşan ince tabakaya hız sınır tabakası denir.
Bir insanın yanındaki hava ısınır, bu da yerçekimi kaynaklı konvektif (taşınım) hava akışına neden olur; bu durum hem bir hız hem de ısıl sınır tabaka ile sonuçlanır. Bir esinti sınır tabakayı bozar; saç ve giysiler ise onu koruyarak insanın daha serin veya daha sıcak hissetmesini sağlar. Bir uçak kanadında, hız sınır tabakası akışın kanada yakın olan kısmıdır; burada viskoz kuvvetler çevredeki viskoz olmayan akışı bozar. Dünya atmosferinde, yere yakın hava katmanıdır (~ 1 km). Bu katman yüzeyden etkilenir; güneşin yeri ısıtmasıyla oluşan gece-gündüz ısı akışları, nem veya yüzeye/yüzeyden momentum transferi bu etkileşime örnektir.
Sınır tabaka türleri
| ]
Laminer sınır tabakalar, yapılarına ve oluştukları koşullara göre kabaca sınıflandırılabilir. Titreşen bir cisim üzerinde gelişen ince kayma tabakası (shear layer) bir örneğidir; ise, üzerine gelen tek yönlü bir akışta tutulan düz bir levha yakınındaki iyi bilinen (similarity) çözümünü ifade eder. ise Blasius profilinin bir genellemesidir. Bir akışkan döndüğünde ve viskoz kuvvetler (konvektif eylemsizlik yerine) Coriolis etkisi ile dengelendiğinde, bir oluşur. Isı transferi teorisinde, bir ısıl sınır tabaka meydana gelir. Bir yüzey aynı anda birden fazla sınır tabaka türüne sahip olabilir.
Hava akışının viskoz doğası, bir yüzey üzerindeki yerel hızları azaltır ve yüzey sürtünmesinden sorumludur. Kanat yüzeyi üzerindeki, viskozite tarafından yavaşlatılan veya durdurulan hava tabakası sınır tabakadır. İki farklı sınır tabaka akışı türü vardır: laminer ve türbülanslı.
Laminer sınır tabaka akışı
Laminer sınır, çok pürüzsüz bir akıştır; türbülanslı sınır tabaka ise girdaplar veya çevrintiler (eddy) içerir. Laminer akış, türbülanslı akıştan daha az yüzey sürtünme direnci yaratır, ancak daha az kararlıdır. Bir kanat yüzeyi üzerindeki sınır tabaka akışı, pürüzsüz bir laminer akış olarak başlar. Akış, hücum kenarından (leading edge) geriye doğru devam ettikçe, laminer sınır tabakanın kalınlığı artar.
Türbülanslı sınır tabaka akışı
Hücum kenarından belli bir mesafe geride, pürüzsüz laminer akış bozulur ve türbülanslı bir akışa geçer. Sürükleme (drag) açısından, laminerden türbülanslı akışa geçişin kanat üzerinde mümkün olduğunca geride olması veya kanat yüzeyinin büyük bir kısmının sınır tabakanın laminer kısmında kalması umulur. Ancak, düşük enerjili laminer akış, türbülanslı tabakadan daha ani bir şekilde bozulma eğilimindedir.
Prandtl sınır tabaka kavramı
| ]

Aerodinamik sınır tabaka kavramı ilk olarak Ludwig Prandtl tarafından 12 Ağustos 1904'te Heidelberg, Almanya'daki üçüncü Uluslararası Matematikçiler Kongresi'nde sunulan bir makalede varsayılmıştır. Bu kavram, akış alanını iki bölgeye ayırarak akışkan akışı denklemlerini basitleştirir: biri sınır tabakanın içinde, viskozitenin baskın olduğu ve sınır cisminin deneyimlediği sürüklemenin çoğunu yaratan bölge; diğeri ise sınır tabakanın dışında, viskozitenin çözüm üzerinde önemli etkiler yaratmadan ihmal edilebildiği bölge. Bu yaklaşım, tam Navier-Stokes denklemlerinde önemli basitleştirmeler yaparak her iki bölgedeki akış için bulunmasına olanak tanır. Aynı hipotez, su gibi orta ila düşük viskoziteye sahip diğer akışkanlar (havanın yanı sıra) için de geçerlidir.
Yüzey ile serbest akışkan arasında bir sıcaklık farkının olduğu durumda, bir cisme veya cisimden ısı transferinin çoğunun hız sınır tabakasının yakınında gerçekleştiği bulunur. Bu durum, denklemlerin sınır tabakanın dışındaki akış alanında basitleştirilmesine tekrar olanak tanır. Sınır tabaka boyunca yüzeye dik yöndeki (örneğin bir kanat profili) basınç dağılımı, sınır tabaka boyunca nispeten sabit kalır ve yüzeyin kendisindeki ile aynıdır.
Hız sınır tabakasının , normalde katı cisimden, viskoz akış hızının serbest akım hızının (bir yüzey hızı) %99'u olduğu noktaya kadar olan mesafe olarak tanımlanır., sınır tabakanın duvarda kaymalı viskoz-olmayan akışa kıyasla kütle akışında bir açığı temsil ettiğini belirten alternatif bir tanımdır. Viskoz olmayan durumda, viskoz durumla aynı toplam kütle akışını sağlamak için duvarın yer değiştirmesi gereken mesafedir. Kaymazlık koşulu, katı bir nesnenin yüzeyindeki akış hızının sıfır olmasını ve akışkan sıcaklığının yüzey sıcaklığına eşit olmasını gerektirir. Akış hızı daha sonra, aşağıda verilen sınır tabaka denklemleri tarafından yönetilerek sınır tabaka içinde hızla artacaktır.
benzer şekilde, cisimden sıcaklığın serbest akım sıcaklığının %99'u olduğu mesafedir. İki kalınlığın oranı Prandtl sayısı tarafından yönetilir. Prandtl sayısı 1 ise, iki sınır tabaka aynı kalınlıktadır. Prandtl sayısı 1'den büyükse, hız sınır tabakası ısıl sınır tabakasından daha kalındır. Prandtl sayısı 1'den küçükse (standart koşullarda hava için geçerli olduğu gibi), hız sınır tabakası ısıl sınır tabakasından daha incedir.
Planörler ve ticari uçaklar gibi yüksek performanslı tasarımlarda, sürüklemeyi en aza indirmek için sınır tabakanın davranışını kontrol etmeye büyük özen gösterilir. İki etkinin dikkate alınması gerekir. Birincisi, sınır tabaka deplasman kalınlığı yoluyla cismin etkin kalınlığını artırır, dolayısıyla basınç sürüklemesini artırır. İkincisi, kanat yüzeyindeki kayma kuvvetleri yaratır.
Tam boyutlu uçakların tipik özelliği olan yüksek Reynolds sayılarında, bir laminer sınır tabakaya sahip olmak arzu edilir. Bu, laminer akışın karakteristik hız profili nedeniyle daha düşük bir yüzey sürtünmesi ile sonuçlanır. Ancak, akış cisim boyunca geliştikçe sınır tabaka kaçınılmaz olarak kalınlaşır ve daha az kararlı hale gelir; sonunda olarak bilinen süreçle türbülanslı hale gelir. Bu problemle başa çıkmanın bir yolu, sınır tabakayı gözenekli bir yüzeyden emmektir (bkz. ). Bu, sürüklemeyi azaltabilir ancak mekanik karmaşıklığı ve havayı hareket ettirmek ve atmak için gereken güç nedeniyle genellikle pratik değildir. Doğal laminer akış teknikleri, kanat profilini veya gövdeyi yeniden şekillendirerek, en kalın noktanın daha geride ve daha az kalın olmasını sağlayarak sınır tabaka geçişini geriye doğru iter. Bu, ön kısımdaki hızları düşürür ve aynı Reynolds sayısı daha büyük bir uzunlukla elde edilir.
Model uçaklarda görülenler gibi daha düşük Reynolds sayılarında, laminer akışı sürdürmek nispeten kolaydır. Bu, arzu edilen düşük yüzey sürtünmesini sağlar. Ancak, laminer sınır tabakaya düşük yüzey sürtünmesini veren hız profili, aynı zamanda onun kötü etkilenmesine neden olur. Basınç, kanat veterinin arka kısmında toparlanmaya başladığında, laminer bir sınır tabaka yüzeyden ayrılma eğiliminde olacaktır. Bu tür bir akış ayrılması, kanat kesitinin etkin boyutunu büyük ölçüde artırdığından, büyük bir artışa neden olur. Bu durumlarda, bir türbülatör kullanarak, laminer ayrılma konumundan önceki bir noktada sınır tabakayı kasıtlı olarak türbülansa "tetiklemek" (trip) avantajlı olabilir. Türbülanslı sınır tabakanın daha dolu hız profili, ayrılmadan ters basınç gradyanına dayanmasını sağlar. Böylece, yüzey sürtünmesi artsa da, genel sürükleme azalır. Bu, golf toplarındaki çukurların ve uçaklardaki arkasındaki prensiptir. Ayrıca, laminer ayrılmanın azaltıldığı veya tamamen ortadan kaldırıldığı basınç toparlanmasını ayarlayan özel kanat kesitleri de tasarlanmıştır. Bu, akış ayrılmasından kaynaklanan basınç sürüklemesi ile indüklenen türbülanstan kaynaklanan yüzey sürtünmesi arasında optimum bir dengeyi temsil eder.
Sınır tabaka denklemleri
| ]Sınır tabaka denklemlerinin türetilmesi, akışkanlar dinamiğindeki en önemli ilerlemelerden biriydi. Bir kullanılarak, viskoz akışkan akışının iyi bilinen yönetici Navier-Stokes denklemleri sınır tabaka içinde büyük ölçüde basitleştirilebilir. Özellikle, kısmi diferansiyel denklemlerin (KDD) , tam Navier-Stokes denklemlerinin eliptik formunun aksine parabolik hale gelir. Bu, denklemlerin çözümünü büyük ölçüde basitleştirir. Sınır tabaka yaklaşımı yapılarak, akış viskoz olmayan bir kısma (birçok yöntemle çözülmesi kolaydır) ve daha kolay çözülebilir bir KDD tarafından yönetilen sınır tabakaya bölünür.
Kartezyen koordinatlarda iki boyutlu kararlı için süreklilik ve Navier-Stokes denklemleri şöyledir:
burada ve hız bileşenleri, yoğunluk, basınç ve akışkanın bir noktadaki (kinematik viskozitesidir).
Yaklaşım, yeterince yüksek bir Reynolds sayısı için bir yüzey üzerindeki akışın, viskoziteden etkilenmeyen bir dış viskoz-olmayan akış bölgesine (akışın çoğunluğu) ve viskozitenin önemli olduğu yüzeye yakın bir bölgeye (sınır tabaka) bölünebileceğini belirtir. ve sırasıyla sınır tabaka içindeki akış yönü ve enine (duvara dik) hızlar olsun. kullanılarak, yukarıdaki hareket denklemlerinin sınır tabaka içinde aşağıdaki hale indirgendiği gösterilebilir:
ve eğer akışkan sıkıştırılamaz ise (standart koşullarda sıvıların olduğu gibi):
Ölçek analizi, akış yönündeki sınır tabaka içindeki enine uzunluk ölçeğinden önemli ölçüde daha büyük olduğunu varsayar. Bundan, akış yönündeki özellik değişimlerinin genellikle duvara dik yöndekilerden çok daha düşük olduğu sonucu çıkar. Bunu süreklilik denklemine uygulamak, duvara dik hız olan 'nin, akış yönü hızı 'ye kıyasla küçük olduğunu gösterir. Statik basınç , 'den bağımsız olduğundan, sınır tabakanın kenarındaki basınç, belirli bir akış yönü konumunda sınır tabaka boyunca olan basınçtır. Dış basınç, Bernoulli denkleminin bir uygulamasıyla elde edilebilir. , sınır tabakanın dışındaki akışkan hızı olsun, burada ve her ikisi de paraleldir. yerine konulduğunda şu sonuç elde edilir:
Statik basınç 'nin akış yönünde değişmediği bir akış için:
böylece sabit kalır. Bu nedenle hareket denklemi şu hale sadeleşir:
Bu yaklaşımlar, bilimsel ve mühendislik açısından ilgi çeken çeşitli pratik akış problemlerinde kullanılır. Yukarıdaki analiz herhangi bir anlık laminer veya türbülanslı sınır tabaka içindir, ancak esas olarak laminer akış çalışmalarında kullanılır çünkü ortalama akış aynı zamanda anlık akıştır (hız dalgalanmaları yoktur). Bu basitleştirilmiş denklem parabolik bir KDD'dir ve genellikle olarak adlandırılan bir benzerlik çözümü kullanılarak çözülebilir.
Prandtl transpozisyon teoremi
| ]Prandtl, sınır tabaka denklemlerini sağlayan herhangi bir çözümünden, yine sınır tabaka denklemlerini sağlayan başka bir çözümünün şu şekilde yazılarak oluşturulabileceğini gözlemledi:
burada keyfidir. Matematiksel açıdan çözüm benzersiz olmadığından, ve tarafından gösterildiği gibi çözüme sonsuz bir özfonksiyon kümesinden herhangi biri eklenebilir.
Von Kármán momentum integrali
| ]Von Kármán, 1921 yılında sınır tabaka denklemini sınır tabaka boyunca entegre ederek integral denklemi türetti. Denklem şöyledir:
burada
- duvar kayma gerilmesi, duvardaki emme/enjeksiyon hızı, deplasman kalınlığı ve momentum kalınlığıdır. Kármán–Pohlhausen yaklaşımı bu denklemden türetilmiştir.
Enerji integrali
| ]Enerji integrali tarafından türetilmiştir.
burada
- sınır tabaka boyunca viskoziteye bağlı enerji yayılım oranı ve enerji kalınlığıdır.
Von Mises dönüşümü
| ]Kararlı iki boyutlu sınır tabakalar için, von Mises, ve yerine bağımsız değişkenler olarak ve 'yi (akım fonksiyonu) alan ve yerine bağımlı değişken 'yi kullanan bir dönüşüm tanıttı. Sınır tabaka denklemi o zaman şu hale gelir:
Orijinal değişkenler şu şekilde geri elde edilir:
Bu dönüşüm daha sonra von Kármán ve tarafından sıkıştırılabilir sınır tabakaya genişletilmiştir.
Crocco dönüşümü
| ]Kararlı iki boyutlu sıkıştırılabilir sınır tabaka için, , ve yerine bağımsız değişkenler olarak ve 'yu alan ve yerine bağımlı değişken 'yi (kayma gerilmesi) kullanan bir dönüşüm tanıttı. Sınır tabaka denklemi o zaman şu hale gelir:
Orijinal koordinat şuradan geri elde edilir:
Türbülanslı sınır tabakalar
| ]Türbülanslı sınır tabakaların ele alınması, akış özelliklerinin zamana bağlı değişimi nedeniyle çok daha zordur. Türbülanslı akışların ele alınmasında en yaygın kullanılan tekniklerden biri (Reynolds decomposition) uygulamaktır. Burada anlık akış özellikleri, ortalama ve dalgalanan (fluctuation) bir bileşene ayrıştırılır; dalgalanan bileşenin ortalamasının her zaman sıfır olduğu varsayılır. Bu tekniğin sınır tabaka denklemlerine uygulanması, literatürde sıkça verilmeyen tam türbülanslı sınır tabaka denklemlerini verir:
Benzer bir ölçek analizi kullanılarak, yukarıdaki denklemler başat terimlere indirgenebilir. Enine yöndeki değişimler için uzunluk ölçeği ve akış yönündeki değişimler için seçilerek (burada ), x-momentumu denklemi şu şekilde basitleşir:
Bu denklem duvardaki kaymazlık koşulunu sağlamaz. Prandtl'ın kendi sınır tabaka denklemleri için yaptığı gibi, viskoz terimin momentum denkleminde başat terim olmasını sağlamak için yeni, daha küçük bir uzunluk ölçeği kullanılmalıdır. y ölçeği olarak seçilerek, bu "iç sınır tabaka" için başat momentum denklemi şu şekilde verilir:
Sonsuz Reynolds sayısı limitinde, basınç gradyanı teriminin türbülanslı sınır tabakanın iç bölgesi üzerinde hiçbir etkisi olmadığı gösterilebilir. Yeni "iç uzunluk ölçeği" viskoz bir uzunluk ölçeğidir ve mertebesindedir; burada , türbülans dalgalanmalarının hız ölçeğidir, bu durumda bir (friction velocity). Laminer sınır tabaka denklemlerinin aksine, farklı akış ölçekleri kümeleri (yani iç ve dış ölçekleme) tarafından yönetilen iki rejimin varlığı, türbülanslı sınır tabaka için evrensel bir benzerlik çözümü bulmayı zor ve tartışmalı hale getirmiştir. Akışın her iki bölgesini de kapsayan bir benzerlik çözümü bulmak için, akışın her iki bölgesinden gelen çözümleri asimptotik olarak eşleştirmek gerekir. Bu tür bir analiz, ya ya da kuvvet yasasını verecektir. Sıkıştırılabilir akışlarda enerji denklemi kullanılarak ısıl sınır tabakalar için de benzer yaklaşımlar uygulanmıştır.
Türbülanslı sınır tabaka denklemlerindeki ek terim , Reynolds kayma gerilmesi olarak bilinir ve a priori (önsel olarak) bilinmemektedir. Bu nedenle türbülanslı sınır tabaka denklemlerinin çözümü, Reynolds kayma gerilmesini bilinen akış değişkenleri veya türevleri cinsinden ifade etmeyi amaçlayan bir kullanılmasını gerektirir. Bu tür modellerin doğruluk ve genellikten yoksun olması, modern akışkanlar dinamiğinde türbülanslı akış özelliklerinin başarılı bir şekilde tahmin edilmesinde büyük bir engeldir. Duvar yakınındaki bölgede sabit bir gerilme tabakası mevcuttur. Dikey hız dalgalanmalarının duvar yakınında sönümlenmesi nedeniyle, terimi ihmal edilebilir hale gelir ve doğrusal bir hız profilinin var olduğunu buluruz. Bu sadece çok duvar yakını bölge için geçerlidir.
Isı ve kütle transferi
| ]1928'de Fransız mühendis André Lévêque, akan bir akışkandaki konvektif ısı transferinin yalnızca yüzeye çok yakın hız değerlerinden etkilendiğini gözlemledi. Büyük Prandtl sayısına sahip akışlar için, yüzeyden serbest akım sıcaklığına sıcaklık/kütle geçişi yüzeye çok yakın çok ince bir bölgede gerçekleşir. Bu nedenle, en önemli akışkan hızları, hız değişiminin yüzeyden normal mesafeyle doğrusal kabul edilebileceği bu çok ince bölge içindekilerdir. Bu şekilde,
için olduğunda,
burada θ, duvarı kesen Poiseuille parabolünün teğetidir. Lévêque'in çözümü bir Poiseuille akışına ısı transferine özgü olsa da, içgörüsü diğer bilim insanlarının ısıl sınır tabaka problemine kesin bir çözüm bulmasına yardımcı oldu. Schuh, bir sınır tabakada u'nun yine y'nin doğrusal bir fonksiyonu olduğunu, ancak bu durumda duvar teğetinin x'in bir fonksiyonu olduğunu gözlemledi. Bunu Lévêque profilinin değiştirilmiş bir versiyonuyla ifade etti:
Bu, düşük sayıları için bile çok iyi bir yaklaşımla sonuçlanır, öyle ki sadece sayısı 1'den çok küçük olan sıvı metaller bu şekilde ele alınamaz.
1962'de Kestin ve Persen, ısıl sınır tabakanın tamamen momentum tabakası içinde olduğu durumlar ve çeşitli duvar sıcaklık dağılımları için ısı transferi çözümlerini açıklayan bir makale yayınladılar.'da bir sıcaklık sıçraması olan düz bir levha problemi için, parabolik ısıl sınır tabaka denklemini bir bayağı diferansiyel denkleme indirgeyen bir ikame önerdiler. Bu denklemin çözümü, yani akışkan içindeki herhangi bir noktadaki sıcaklık, eksik bir gama fonksiyonu olarak ifade edilebilir., ısıl sınır tabaka denklemini çözümü aynı eksik gama fonksiyonu olan bir bayağı diferansiyel denkleme indirgeyen eşdeğer bir ikame önerdi. Isı iletimini içeren sıkıştırılamaz sınır tabaka denklemleri için zamana bağlı (self-similarity) ansatz (tahmin yürüterek hesaplama) ile analitik çözümler türetilebilir.
Çeşitli ders kitaplarından iyi bilindiği üzere, sınır tabakanın artmasıyla ısı transferi azalma eğilimindedir. Yakın zamanda, bir fotovoltaik jeneratörden geçen rüzgarın, azalan ısı transferi nedeniyle türbülanslı bir rejim altında PV panellerindeki ısıyı "hapsetme" eğiliminde olduğu pratik ve büyük ölçekte gözlemlendi. Sıklıkla doğası gereği türbülanslı olduğu varsayılmasına rağmen, bu tesadüfi gözlem, doğal rüzgarın pratikte ideal bir akışkana çok yakın davrandığını, en azından düz bir levhadaki beklenen davranışa benzeyen bir gözlemde, bu tür fenomenlerin daha büyük ölçekte analiz edilmesindeki zorluğu potansiyel olarak azalttığını göstermektedir.
Sınır tabaka analizinden konvektif transfer sabitleri
| ], yukarıdaki denklemleri için kesin bir çözüm türetti. Sınır tabaka , laminer akış için Reynolds sayısının bir fonksiyonudur.
- = sınır tabakanın kalınlığı: hızın uzak alan hızı 'un %99'undan az olduğu akış bölgesi;
yarı sonsuz levha boyunca konum, ve ise ile verilen Reynolds Sayısıdır ( yoğunluk ve dinamik viskozite).
Blasius çözümü sınır koşullarını boyutsuz bir formda kullanır:
- 'da
- 'da ve 'da

Birçok durumda, kaymazlık sınır koşulunun, levha yüzeyindeki akışkan hızı 'nin tüm konumlarda levhanın hızına eşit olduğunu kabul ettiğine dikkat edin. Eğer levha hareket etmiyorsa, o zaman olur. Akışkan kaymasına izin verilirse çok daha karmaşık bir türetme gerekir.
Aslında, yarı sonsuz bir levha üzerindeki sınır tabakadaki laminer hız profili için Blasius çözümü, sırasıyla ısı ve kütle transferi için Isıl ve Konsantrasyon sınır tabakalarını tanımlamak üzere kolayca genişletilebilir. Diferansiyel x-momentum dengesi (hareket denklemi) yerine, bu benzer şekilde türetilmiş Enerji ve Kütle dengesini kullanır:
Enerji:
Kütle:
Momentum dengesi için, kinematik viskozite , momentum difüzivitesi (yayılımı) olarak kabul edilebilir. Enerji dengesinde bunun yerini ısıl difüzivite , kütle dengesinde ise kütle difüzivitesi alır. Bir maddenin , onun ısıl iletkenliği, yoğunluğu ve ısı kapasitesidir. AB indisi, A türünün B türüne difüzyonunu (yayılımını) belirtir.
varsayımı altında, bu denklemler momentum dengesine eşdeğer hale gelir. Böylece, Prandtl sayısı ve Schmidt sayısı için Blasius çözümü doğrudan geçerlidir. Buna göre, bu türetme 'yi veya (mutlak sıcaklık veya A türünün konsantrasyonu) ile değiştirerek sınır koşullarının ilgili bir formunu kullanır. S indisi bir yüzey koşulunu belirtir.
- 'da
- 'da ve 'da
Akım çizgisi fonksiyonunu kullanarak Blasius, levha yüzeyindeki kayma gerilmesi için aşağıdaki çözümü elde etti:
Ve sınır koşulları aracılığıyla, şunlar bilinmektedir:
Levha yüzeyinden dışarı ısı/kütle akısı için aşağıdaki ilişkiler verilir:
Böylece için
burada , ve 'nın uzak alan değerlerinin %99'undan az olduğu akış bölgeleridir.
Belirli bir akışkanın Prandtl sayısı genellikle bir olmadığından, Ludwig Prandtl ile çalışan Alman mühendis E. Pohlhausen, bu denklemleri için geçerli olacak şekilde ampirik olarak genişletmeye çalıştı. Sonuçları 'ye de uygulanabilir. Prandtl sayısının 0,6'dan büyük olması durumunda, yaklaşık olarak şu şekilde verildiğini buldu:

- ve bu nedenle
Bu çözümden, konvektif ısı/kütle transferi sabitlerini sınır tabaka akış bölgesine dayanarak karakterize etmek mümkündür. (Fourier iletim yasası) ve (Newton'un Soğuma Yasası), yukarıda türetilen akı terimi ve sınır tabaka kalınlığı ile birleştirilir.
Bu, yarı sonsuz düzlem üzerindeki bir noktadaki yerel konvektif sabit 'i verir. Levhanın uzunluğu boyunca entegrasyon bir ortalama verir:
Kütle transferi terimleriyle ( = konvektif kütle transferi sabiti, = A türünün B türüne difüzivitesi, ) türetme izlendiğinde, aşağıdaki çözümler elde edilir:
Bu çözümler, Prandtl/Schmidt sayısı 0,6'dan büyük olan laminer akış için geçerlidir.
Gemi inşa mühendisliği
| ]Uçaklar için geçerli olan prensiplerin çoğu, hava yerine birincil akışkan olarak suyun söz konusu olduğu gemiler, denizaltılar ve açık deniz platformları için de geçerlidir. Su ideal bir akışkan olmadığından, suda hareket eden gemiler dirençle karşılaşır. Akışkan parçacıkları, su ile gemi arasındaki yapışma kuvveti nedeniyle geminin tekne gövdesine yapışır ve akış hızının küçük ama dik bir hız gradyanı oluşturduğu bir sınır tabaka meydana getirir; gemiyle temas halindeki akışkan ideal olarak 0 bağıl hıza sahipken, sınır tabakanın sınırındaki akışkan hızına veya akışkanın gemi etrafındaki bağıl hızına sahiptir.
Geminin önü, çevresindeki akışkan nedeniyle normal basınç kuvvetleriyle karşılaşırken, arka kısım sınır tabaka nedeniyle daha düşük bir etkiyen basınç bileşeni görür. Bu durum, 'viskoz basınç sürüklemesi' veya 'form sürüklemesi' olarak bilinen basınç kaynaklı daha yüksek bir dirence yol açar.
Gemiler için, uçakların aksine, su yoğunluğundaki değişimin ihmal edilebilir olduğu sıkıştırılamaz akışlarla ilgilenilir (1000 kPa'ya yakın bir basınç artışı yalnızca 2–3 kg/m3'lük bir değişime yol açar). Bu akışkanlar dinamiği alanına hidrodinamik denir. Bir gemi mühendisi önce hidrodinamik için, sonra mukavemet için tasarım yapar. Sınır tabaka gelişimi, bozulması ve ayrılması kritiktir çünkü suyun yüksek viskozitesi yüksek kayma gerilmeleri üretir.
Sınır tabaka türbini
| ]Bu etki, 1913 yılında Nikola Tesla tarafından patenti alınan kullanılmıştır. Geleneksel bir türbinde olduğu gibi kanatlara çarpan bir akışkan değil, sınır tabaka etkisini kullandığı için kanatsız türbin olarak adlandırılır. Sınır tabaka türbinleri aynı zamanda kohezyon tipi türbin, kanatsız türbin ve Prandtl tabakası türbini (Ludwig Prandtl'a atıfla) olarak da bilinir.
Boyut analizi kullanarak bir silindirdeki geçici sınır tabaka kalınlığının tahmini
| ]Silindirik bir akış için geçici ve viskoz kuvvet denklemlerini kullanarak, Womersley Sayısını () bularak geçici sınır tabaka kalınlığını tahmin edebilirsiniz.
Geçici Kuvvet =
Viskoz Kuvvet =
Bunları birbirine eşitlemek şunu verir:
Delta için çözüm:
Boyutsuz formda:
burada = Womersley Sayısı; = yoğunluk; = hız; salınım frekansı; = geçici sınır tabakanın uzunluğu; = viskozite; = karakteristik uzunluk.
Boyut analizi kullanarak bir silindirdeki sınır tabakada konvektif akış koşullarının tahmini
| ]Silindirik bir akış için sınır tabakadaki konvektif ve viskoz kuvvet denklemlerini kullanarak, boyutsuz Reynolds Sayısını () bularak sınır tabakadaki konvektif akış koşullarını tahmin edebilirsiniz.
Konvektif kuvvet:
Viskoz kuvvet:
Bunları birbirine eşitlemek şunu verir:
Delta için çözüm:
Boyutsuz formda:
burada = Reynolds Sayısı; = yoğunluk; = hız; = konvektif sınır tabakanın uzunluğu; = viskozite; = karakteristik uzunluk.
Sınır tabaka yutulması
| ]Sınır tabaka yutulması, yavaş gövde sınır tabakasını yutan ve sürüklemeyi azaltmak ve artırmak için iz bölgesini yeniden enerjelendiren kıça monte edilmiş bir ile bir artış vaat etmektedir. Bozuk hava akışında çalışmak için fan daha ağırdır, verimliliği azalır ve entegrasyonu zordur. veya Fransız araştırma ajansı 'nın Nova konsepti gibi tasarımlarda, gövde sınır tabakasının %40'ını yutarak seyir sırasında %5 tasarruf sağlamak için kullanılır.
Airbus, Nautilius konseptini Eylül 2018'deki ICAS kongresinde sundu: azimut akış bozulmasını en aza indirirken tüm gövde sınır tabakasını yutmak için, gövde 13-18:1 fanlara sahip iki iğe ayrılır. İtici verimlilikleri, daha küçük, daha hafif, daha az karmaşık ve gürültülü motorlara sahip zıt yönlü dönen gibi %90'a kadar çıkar. Normal bir kanat altı 15:1 baypas oranlı motora kıyasla yakıt tüketimini %10'dan fazla düşürebilir.
Ayrıca bakınız
| ]Kaynakça
| ]- ^ Young, A.D. (1989). Boundary layers. 1st publ. Washington, DC: American Institute of Aeronautics and Astronautics. ISBN .
- ^ Schlichting, Hermann; Gersten, Klaus (2017). "2.1 Boundary–Layer Concept". Boundary-Layer theory. Ninth. Berlin Heidelberg: Springer. s. 29. doi:10.1007/978-3-662-52919-5_2. ISBN . Erişim tarihi: 5 Ağustos 2023.
Sıklıkla sınır, keyfi olarak hızın dış hızın belirli bir yüzdesine ulaştığı nokta olarak verilir, örn. %99. Açıklık için genellikle bir indis kullanılır, örn. δ99.
- ^ Prandtl, L. (1938). "Zur Berechnung der Grenzschichten". Zeitschrift für Angewandte Mathematik und Mechanik. 18 (1). ss. 77-82. Bibcode:1938ZaMM...18...77P. doi:10.1002/zamm.19380180111.
- ^ Van Dyke, Milton. Perturbation methods in fluid mechanics. Parabolic Press, Incorporated, 1975.
- ^ Stewartson, K. (1957). "On Asymptotic Expansions in the Theory of Boundary Layers". Journal of Mathematics and Physics. 36 (1–4). ss. 173-191. doi:10.1002/sapm1957361173.
- ^ Libby, Paul A.; Fox, Herbert (1963). "Some perturbation solutions in laminar boundary-layer theory". Journal of Fluid Mechanics. 17 (3). s. 433. doi:10.1017/S0022112063001439.
- ^ Fox, Herbert; Libby, Paul A. (1964). "Some perturbation solutions in laminar boundary layer theory Part 2. The energy equation". Journal of Fluid Mechanics. 19 (3). ss. 433-451. Bibcode:1964JFM....19..433F. doi:10.1017/S0022112064000830.
- ^ von Kármán, T. (1921). "Über laminare und turbulente Reibung". Zeitschrift für Angewandte Mathematik und Mechanik. 1 (4). ss. 233-252. Bibcode:1921ZaMM....1..233K. doi:10.1002/zamm.19210010401.
- ^ Wieghardt, K. On an energy equation for the calculation of laminar boundary layers. Joint Intelligence Objectives Agency, 1946.
- ^ Wieghardt, K. (1948). "Über einen Energiesatz zur Berechnung laminarer Grenzschichten". Ingenieur-Archiv. 16 (3–4). ss. 231-242. Bibcode:1948AAM....16..231W. doi:10.1007/BF00548007.
- ^ Rosenhead, Louis, ed. Laminar boundary layers. Clarendon Press, 1963.
- ^ Tollmien, Walter; Schlichting, Hermann; Görtler, Henry; Riegels, F. W. (1961). "Bemerkungen zur Hydrodynamik". Ludwig Prandtl Gesammelte Abhandlungen. ss. 627-631. doi:10.1007/978-3-662-11836-8_49. ISBN .
- ^ von Kármán, T.; Tsien, H. S. (1938). "Boundary Layer in Compressible Fluids". Journal of the Aeronautical Sciences. 5 (6). ss. 227-232. doi:10.2514/8.591.
- ^ Crocco, L. "A characteristic transformation of the equations of the boundary layer in gases." ARC 4582 (1939): 1940.
- ^ von Karman, T. (1939). "The analogy between fluid friction and heat transfer". Transactions of the American Society of Mechanical Engineers. 61 (8). ss. 705-710. doi:10.1115/1.4021298.
- ^ Guo, J.; Yang, X. I. A.; Ihme, M. (March 2022). "Structure of the thermal boundary layer in turbulent channel flows at transcritical conditions". Journal of Fluid Mechanics (İngilizce). Cilt 934. Bibcode:2022JFM...934A..45G. doi:10.1017/jfm.2021.1157
 . ISSN 0022-1120.
. ISSN 0022-1120. - ^ Lévêque, A. (1928). "Les lois de la transmission de chaleur par convection". Annales des Mines ou Recueil de Mémoires sur l'Exploitation des Mines et sur les Sciences et les Arts qui s'y Rattachent, Mémoires (Fransızca). XIII (13). ss. 201-239.
- ^ a b Niall McMahon. "André Lévêque p285, a review of his velocity profile approximation". 4 Haziran 2012 tarihinde kaynağından arşivlendi.
- ^ a b Martin, H. (2002). "The generalized Lévêque equation and its practical use for the prediction of heat and mass transfer rates from pressure drop". Chemical Engineering Science. 57 (16). ss. 3217-3223. Bibcode:2002ChEnS..57.3217M. doi:10.1016/S0009-2509(02)00194-X.
- ^ Schuh, H. (1953). "On Asymptotic Solutions for the Heat Transfer at Varying Wall Temperatures in a Laminar Boundary Layer with Hartree's Velocity Profiles". Journal of the Aeronautical Sciences. 20 (2). ss. 146-147. doi:10.2514/8.2566.
- ^ Kestin, J.; Persen, L.N. (1962). "The transfer of heat across a turbulent boundary layer at very high prandtl numbers". International Journal of Heat and Mass Transfer. 5 (5). ss. 355-371. Bibcode:1962IJHMT...5..355K. doi:10.1016/0017-9310(62)90026-1.
- ^ Schlichting, H. (1979). Boundary-Layer Theory. 7. New York (USA): McGraw-Hill.
- ^ Barna, Imre Ferenc; Bognár, Gabriella; Mátyás, László; Hriczó, Krisztián (2022). "Self‑similar analysis of the time‑dependent compressible and incompressible boundary layers including heat conduction". Journal of Thermal Analysis and Calorimetry. Cilt 147. ss. 13625-13632. arXiv:2101.08990
 . doi:10.1007/s10973-022-11574-3.
. doi:10.1007/s10973-022-11574-3. - ^ Rossa, Carlos (2023). "Energy losses in photovoltaic generators due to wind patterns". Nature Communications Engineering. 2 (66). Bibcode:2023CmEng...2...66R. doi:10.1038/s44172-023-00119-7. (PMC) 10956078
 .
. - ^ Blasius, H. (1908). "Grenzschichten in Flüssigkeiten mit kleiner Reibung". Zeitschrift für Mathematik und Physik. Cilt 56. ss. 1-37. (İngilizce çeviri)
- ^ Martin, Michael J. (2001). "Blasius boundary layer solution with slip flow conditions". AIP Conference Proceedings. 585. ss. 518-523. doi:10.1063/1.1407604. hdl:2027.42/87372.
- ^ a b Geankoplis, Christie J. Transport Processes and Separation Process Principles: (includes Unit Operations). Fourth ed. Upper Saddle River, NJ: Prentice Hall Professional Technical Reference, 2003. Print.
- ^ Pohlhausen, E. (1921). "Der Wärmeaustausch zwischen festen Körpern und Flüssigkeiten mit kleiner reibung und kleiner Wärmeleitung". Zeitschrift für Angewandte Mathematik und Mechanik. 1 (2). ss. 115-121. Bibcode:1921ZaMM....1..115P. doi:10.1002/zamm.19210010205.
- ^ a b "Resistance and Powering of Ships" (PDF). usna.edu. Erişim tarihi: 14 Şubat 2024.
- ^ a b c Graham Warwick (19 Kasım 2018). "The Week In Technology, November 19-23, 2018". Aviation Week & Space Technology.
- (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages. ISBN .
- A.D. Polyanin and V.F. Zaitsev, Handbook of Nonlinear Partial Differential Equations, Chapman & Hall/CRC Press, Boca Raton – London, 2004.
- A.D. Polyanin, A.M. Kutepov, A.V. Vyazmin, and D.A. Kazenin, Hydrodynamics, Mass and Heat Transfer in Chemical Engineering, Taylor & Francis, London, 2002.
- Hermann Schlichting, Klaus Gersten, E. Krause, H. Jr. Oertel, C. Mayes "Boundary-Layer Theory" 8th edition Springer 2004
- John D. Anderson Jr., "Ludwig Prandtl's Boundary Layer", Physics Today, December 2005
- Anderson, John (1992). Fundamentals of Aerodynamics. 2nd. Toronto: S.S.CHAND. ss. 711-714. ISBN .
- and , "A First Course in Turbulence", The MIT Press, (1972).
- Lectures in Turbulence for the 21st Century by William K. George
Dış bağlantılar
| ]- National Science Digital Library – Boundary Layer
- Moore, Franklin K., "Displacement effect of a three-dimensional boundary layer". NACA Report 1124, 1953.
- Benson, Tom, "Boundary layer". NASA Glenn Learning Technologies.
- Boundary layer separation
- Boundary layer equations: Exact Solutions – from EqWorld
- Jones, T.V. BOUNDARY LAYER HEAT TRANSFER
- "The revolutionary concept of "boundary layer" and its prevalence in aeronautics by Sourabh S. Diwan". YouTube. International Centre for Theoretical Sciences. 18 Şubat 2022.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Vikipedi ozgur ansiklopedi sayfasindan yonlendirildi Bir insan elinin etrafindaki sinir tabakayi gosteren Sinir tabaka elin arkasinda en belirgin olan parlak yesil sinirdir yuksek cozunurluklu goruntu icin tiklayin Fizik ve akiskanlar mekaniginde bir sinir tabaka veya sinir katman bir yuzey boyunca akan akiskanin olusturdugu sinir yuzeyinin hemen yakinindaki ince akiskan tabakasidir Akiskanin duvar ile etkilesimi bir kaymazlik sinir kosuluna duvarda sifir hiz neden olur Akis hizi daha sonra yuzeyden uzaklastikca serbest akim hizina ulasana kadar monoton bir sekilde artar Hizi henuz serbest akim hizina donmemis olan akiskandan olusan ince tabakaya hiz sinir tabakasi denir Bir insanin yanindaki hava isinir bu da yercekimi kaynakli konvektif tasinim hava akisina neden olur bu durum hem bir hiz hem de isil sinir tabaka ile sonuclanir Bir esinti sinir tabakayi bozar sac ve giysiler ise onu koruyarak insanin daha serin veya daha sicak hissetmesini saglar Bir ucak kanadinda hiz sinir tabakasi akisin kanada yakin olan kismidir burada viskoz kuvvetler cevredeki viskoz olmayan akisi bozar Dunya atmosferinde yere yakin hava katmanidir 1 km Bu katman yuzeyden etkilenir gunesin yeri isitmasiyla olusan gece gunduz isi akislari nem veya yuzeye yuzeyden momentum transferi bu etkilesime ornektir Sinir tabaka turleri span Laminer akistan turbulansli akisa gecisi gosteren bir sinir tabaka gorsellestirmesi Laminer sinir tabakalar yapilarina ve olustuklari kosullara gore kabaca siniflandirilabilir Titresen bir cisim uzerinde gelisen ince kayma tabakasi shear layer bir ornegidir ise uzerine gelen tek yonlu bir akista tutulan duz bir levha yakinindaki iyi bilinen similarity cozumunu ifade eder ise Blasius profilinin bir genellemesidir Bir akiskan dondugunde ve viskoz kuvvetler konvektif eylemsizlik yerine Coriolis etkisi ile dengelendiginde bir olusur Isi transferi teorisinde bir isil sinir tabaka meydana gelir Bir yuzey ayni anda birden fazla sinir tabaka turune sahip olabilir Hava akisinin viskoz dogasi bir yuzey uzerindeki yerel hizlari azaltir ve yuzey surtunmesinden sorumludur Kanat yuzeyi uzerindeki viskozite tarafindan yavaslatilan veya durdurulan hava tabakasi sinir tabakadir Iki farkli sinir tabaka akisi turu vardir laminer ve turbulansli Laminer sinir tabaka akisi Laminer sinir cok puruzsuz bir akistir turbulansli sinir tabaka ise girdaplar veya cevrintiler eddy icerir Laminer akis turbulansli akistan daha az yuzey surtunme direnci yaratir ancak daha az kararlidir Bir kanat yuzeyi uzerindeki sinir tabaka akisi puruzsuz bir laminer akis olarak baslar Akis hucum kenarindan leading edge geriye dogru devam ettikce laminer sinir tabakanin kalinligi artar Turbulansli sinir tabaka akisi Hucum kenarindan belli bir mesafe geride puruzsuz laminer akis bozulur ve turbulansli bir akisa gecer Surukleme drag acisindan laminerden turbulansli akisa gecisin kanat uzerinde mumkun oldugunca geride olmasi veya kanat yuzeyinin buyuk bir kisminin sinir tabakanin laminer kisminda kalmasi umulur Ancak dusuk enerjili laminer akis turbulansli tabakadan daha ani bir sekilde bozulma egilimindedir Prandtl sinir tabaka kavrami span Ludwig PrandtlLaminer sinir tabaka hiz profili Aerodinamik sinir tabaka kavrami ilk olarak Ludwig Prandtl tarafindan 12 Agustos 1904 te Heidelberg Almanya daki ucuncu Uluslararasi Matematikciler Kongresi nde sunulan bir makalede varsayilmistir Bu kavram akis alanini iki bolgeye ayirarak akiskan akisi denklemlerini basitlestirir biri sinir tabakanin icinde viskozitenin baskin oldugu ve sinir cisminin deneyimledigi suruklemenin cogunu yaratan bolge digeri ise sinir tabakanin disinda viskozitenin cozum uzerinde onemli etkiler yaratmadan ihmal edilebildigi bolge Bu yaklasim tam Navier Stokes denklemlerinde onemli basitlestirmeler yaparak her iki bolgedeki akis icin bulunmasina olanak tanir Ayni hipotez su gibi orta ila dusuk viskoziteye sahip diger akiskanlar havanin yani sira icin de gecerlidir Yuzey ile serbest akiskan arasinda bir sicaklik farkinin oldugu durumda bir cisme veya cisimden isi transferinin cogunun hiz sinir tabakasinin yakininda gerceklestigi bulunur Bu durum denklemlerin sinir tabakanin disindaki akis alaninda basitlestirilmesine tekrar olanak tanir Sinir tabaka boyunca yuzeye dik yondeki ornegin bir kanat profili basinc dagilimi sinir tabaka boyunca nispeten sabit kalir ve yuzeyin kendisindeki ile aynidir Hiz sinir tabakasinin normalde kati cisimden viskoz akis hizinin serbest akim hizinin bir yuzey hizi 99 u oldugu noktaya kadar olan mesafe olarak tanimlanir sinir tabakanin duvarda kaymali viskoz olmayan akisa kiyasla kutle akisinda bir acigi temsil ettigini belirten alternatif bir tanimdir Viskoz olmayan durumda viskoz durumla ayni toplam kutle akisini saglamak icin duvarin yer degistirmesi gereken mesafedir Kaymazlik kosulu kati bir nesnenin yuzeyindeki akis hizinin sifir olmasini ve akiskan sicakliginin yuzey sicakligina esit olmasini gerektirir Akis hizi daha sonra asagida verilen sinir tabaka denklemleri tarafindan yonetilerek sinir tabaka icinde hizla artacaktir benzer sekilde cisimden sicakligin serbest akim sicakliginin 99 u oldugu mesafedir Iki kalinligin orani Prandtl sayisi tarafindan yonetilir Prandtl sayisi 1 ise iki sinir tabaka ayni kalinliktadir Prandtl sayisi 1 den buyukse hiz sinir tabakasi isil sinir tabakasindan daha kalindir Prandtl sayisi 1 den kucukse standart kosullarda hava icin gecerli oldugu gibi hiz sinir tabakasi isil sinir tabakasindan daha incedir Planorler ve ticari ucaklar gibi yuksek performansli tasarimlarda suruklemeyi en aza indirmek icin sinir tabakanin davranisini kontrol etmeye buyuk ozen gosterilir Iki etkinin dikkate alinmasi gerekir Birincisi sinir tabaka deplasman kalinligi yoluyla cismin etkin kalinligini artirir dolayisiyla basinc suruklemesini artirir Ikincisi kanat yuzeyindeki kayma kuvvetleri yaratir Tam boyutlu ucaklarin tipik ozelligi olan yuksek Reynolds sayilarinda bir laminer sinir tabakaya sahip olmak arzu edilir Bu laminer akisin karakteristik hiz profili nedeniyle daha dusuk bir yuzey surtunmesi ile sonuclanir Ancak akis cisim boyunca gelistikce sinir tabaka kacinilmaz olarak kalinlasir ve daha az kararli hale gelir sonunda olarak bilinen surecle turbulansli hale gelir Bu problemle basa cikmanin bir yolu sinir tabakayi gozenekli bir yuzeyden emmektir bkz Bu suruklemeyi azaltabilir ancak mekanik karmasikligi ve havayi hareket ettirmek ve atmak icin gereken guc nedeniyle genellikle pratik degildir Dogal laminer akis teknikleri kanat profilini veya govdeyi yeniden sekillendirerek en kalin noktanin daha geride ve daha az kalin olmasini saglayarak sinir tabaka gecisini geriye dogru iter Bu on kisimdaki hizlari dusurur ve ayni Reynolds sayisi daha buyuk bir uzunlukla elde edilir Model ucaklarda gorulenler gibi daha dusuk Reynolds sayilarinda laminer akisi surdurmek nispeten kolaydir Bu arzu edilen dusuk yuzey surtunmesini saglar Ancak laminer sinir tabakaya dusuk yuzey surtunmesini veren hiz profili ayni zamanda onun kotu etkilenmesine neden olur Basinc kanat veterinin arka kisminda toparlanmaya basladiginda laminer bir sinir tabaka yuzeyden ayrilma egiliminde olacaktir Bu tur bir akis ayrilmasi kanat kesitinin etkin boyutunu buyuk olcude artirdigindan buyuk bir artisa neden olur Bu durumlarda bir turbulator kullanarak laminer ayrilma konumundan onceki bir noktada sinir tabakayi kasitli olarak turbulansa tetiklemek trip avantajli olabilir Turbulansli sinir tabakanin daha dolu hiz profili ayrilmadan ters basinc gradyanina dayanmasini saglar Boylece yuzey surtunmesi artsa da genel surukleme azalir Bu golf toplarindaki cukurlarin ve ucaklardaki arkasindaki prensiptir Ayrica laminer ayrilmanin azaltildigi veya tamamen ortadan kaldirildigi basinc toparlanmasini ayarlayan ozel kanat kesitleri de tasarlanmistir Bu akis ayrilmasindan kaynaklanan basinc suruklemesi ile induklenen turbulanstan kaynaklanan yuzey surtunmesi arasinda optimum bir dengeyi temsil eder Sinir tabaka denklemleri span Sinir tabaka denklemlerinin turetilmesi akiskanlar dinamigindeki en onemli ilerlemelerden biriydi Bir kullanilarak viskoz akiskan akisinin iyi bilinen yonetici Navier Stokes denklemleri sinir tabaka icinde buyuk olcude basitlestirilebilir Ozellikle kismi diferansiyel denklemlerin KDD tam Navier Stokes denklemlerinin eliptik formunun aksine parabolik hale gelir Bu denklemlerin cozumunu buyuk olcude basitlestirir Sinir tabaka yaklasimi yapilarak akis viskoz olmayan bir kisma bircok yontemle cozulmesi kolaydir ve daha kolay cozulebilir bir KDD tarafindan yonetilen sinir tabakaya bolunur Kartezyen koordinatlarda iki boyutlu kararli icin sureklilik ve Navier Stokes denklemleri soyledir u x y y 0 displaystyle partial u over partial x partial upsilon over partial y 0 u u x y u y 1r p x n 2u x2 2u y2 displaystyle u partial u over partial x upsilon partial u over partial y 1 over rho partial p over partial x nu left partial 2 u over partial x 2 partial 2 u over partial y 2 right u y x y y y 1r p y n 2y x2 2y y2 displaystyle u partial upsilon over partial x upsilon partial upsilon over partial y 1 over rho partial p over partial y nu left partial 2 upsilon over partial x 2 partial 2 upsilon over partial y 2 right burada u displaystyle u ve y displaystyle upsilon hiz bilesenleri r displaystyle rho yogunluk p displaystyle p basinc ve n displaystyle nu akiskanin bir noktadaki kinematik viskozitesidir Yaklasim yeterince yuksek bir Reynolds sayisi icin bir yuzey uzerindeki akisin viskoziteden etkilenmeyen bir dis viskoz olmayan akis bolgesine akisin cogunlugu ve viskozitenin onemli oldugu yuzeye yakin bir bolgeye sinir tabaka bolunebilecegini belirtir u displaystyle u ve y displaystyle upsilon sirasiyla sinir tabaka icindeki akis yonu ve enine duvara dik hizlar olsun kullanilarak yukaridaki hareket denklemlerinin sinir tabaka icinde asagidaki hale indirgendigi gosterilebilir u u x y u y 1r p x n 2u y2 displaystyle u partial u over partial x upsilon partial u over partial y 1 over rho partial p over partial x nu partial 2 u over partial y 2 1r p y 0 displaystyle 1 over rho partial p over partial y 0 ve eger akiskan sikistirilamaz ise standart kosullarda sivilarin oldugu gibi u x y y 0 displaystyle partial u over partial x partial upsilon over partial y 0 Olcek analizi akis yonundeki sinir tabaka icindeki enine uzunluk olceginden onemli olcude daha buyuk oldugunu varsayar Bundan akis yonundeki ozellik degisimlerinin genellikle duvara dik yondekilerden cok daha dusuk oldugu sonucu cikar Bunu sureklilik denklemine uygulamak duvara dik hiz olan y displaystyle upsilon nin akis yonu hizi u displaystyle u ye kiyasla kucuk oldugunu gosterir Statik basinc p displaystyle p y displaystyle y den bagimsiz oldugundan sinir tabakanin kenarindaki basinc belirli bir akis yonu konumunda sinir tabaka boyunca olan basinctir Dis basinc Bernoulli denkleminin bir uygulamasiyla elde edilebilir U displaystyle U sinir tabakanin disindaki akiskan hizi olsun burada u displaystyle u ve U displaystyle U her ikisi de paraleldir p displaystyle p yerine konuldugunda su sonuc elde edilir u u x y u y UdUdx n 2u y2 displaystyle u partial u over partial x upsilon partial u over partial y U frac dU dx nu partial 2 u over partial y 2 Statik basinc p displaystyle p nin akis yonunde degismedigi bir akis icin dpdx 0 displaystyle frac dp dx 0 boylece U displaystyle U sabit kalir Bu nedenle hareket denklemi su hale sadelesir u u x y u y n 2u y2 displaystyle u partial u over partial x upsilon partial u over partial y nu partial 2 u over partial y 2 Bu yaklasimlar bilimsel ve muhendislik acisindan ilgi ceken cesitli pratik akis problemlerinde kullanilir Yukaridaki analiz herhangi bir anlik laminer veya turbulansli sinir tabaka icindir ancak esas olarak laminer akis calismalarinda kullanilir cunku ortalama akis ayni zamanda anlik akistir hiz dalgalanmalari yoktur Bu basitlestirilmis denklem parabolik bir KDD dir ve genellikle olarak adlandirilan bir benzerlik cozumu kullanilarak cozulebilir Prandtl transpozisyon teoremi span Prandtl sinir tabaka denklemlerini saglayan herhangi bir u x y t v x y t displaystyle u x y t v x y t cozumunden yine sinir tabaka denklemlerini saglayan baska bir u x y t v x y t displaystyle u x y t v x y t cozumunun su sekilde yazilarak olusturulabilecegini gozlemledi u x y t u x y f x t v x y t v x y f x t f x u x y f x t displaystyle u x y t u x y f x t quad v x y t v x y f x t f x u x y f x t burada f x displaystyle f x keyfidir Matematiksel acidan cozum benzersiz olmadigindan ve tarafindan gosterildigi gibi cozume sonsuz bir ozfonksiyon kumesinden herhangi biri eklenebilir Von Karman momentum integrali span Von Karman 1921 yilinda sinir tabaka denklemini sinir tabaka boyunca entegre ederek integral denklemi turetti Denklem soyledir twrU2 1U2 t Ud1 d2 x 2d2 d1U U x vwU displaystyle frac tau w rho U 2 frac 1 U 2 frac partial partial t U delta 1 frac partial delta 2 partial x frac 2 delta 2 delta 1 U frac partial U partial x frac v w U burada tw m u y y 0 vw v x 0 t d1 0 1 uU dy d2 0 uU 1 uU dy displaystyle tau w mu left frac partial u partial y right y 0 quad v w v x 0 t quad delta 1 int 0 infty left 1 frac u U right dy quad delta 2 int 0 infty frac u U left 1 frac u U right dy tw displaystyle tau w duvar kayma gerilmesi vw displaystyle v w duvardaki emme enjeksiyon hizi d1 displaystyle delta 1 deplasman kalinligi ve d2 displaystyle delta 2 momentum kalinligidir Karman Pohlhausen yaklasimi bu denklemden turetilmistir Enerji integrali span Enerji integrali tarafindan turetilmistir 2erU3 1U t d1 d2 2d2U2 U t 1U3 x U3d3 vwU displaystyle frac 2 varepsilon rho U 3 frac 1 U frac partial partial t delta 1 delta 2 frac 2 delta 2 U 2 frac partial U partial t frac 1 U 3 frac partial partial x U 3 delta 3 frac v w U burada e 0 m u y 2dy d3 0 uU 1 u2U2 dy displaystyle varepsilon int 0 infty mu left frac partial u partial y right 2 dy quad delta 3 int 0 infty frac u U left 1 frac u 2 U 2 right dy e displaystyle varepsilon sinir tabaka boyunca viskoziteye bagli enerji yayilim orani ve d3 displaystyle delta 3 enerji kalinligidir Von Mises donusumu span Kararli iki boyutlu sinir tabakalar icin von Mises x displaystyle x ve y displaystyle y yerine bagimsiz degiskenler olarak x displaystyle x ve ps displaystyle psi yi akim fonksiyonu alan ve u displaystyle u yerine bagimli degisken x U2 u2 displaystyle chi U 2 u 2 yi kullanan bir donusum tanitti Sinir tabaka denklemi o zaman su hale gelir x x nU2 x 2x ps2 displaystyle frac partial chi partial x nu sqrt U 2 chi frac partial 2 chi partial psi 2 Orijinal degiskenler su sekilde geri elde edilir y U2 xdps u U2 x v u x 1u dps displaystyle y int sqrt U 2 chi d psi quad u sqrt U 2 chi quad v u int frac partial partial x left frac 1 u right d psi Bu donusum daha sonra von Karman ve tarafindan sikistirilabilir sinir tabakaya genisletilmistir Crocco donusumu span Kararli iki boyutlu sikistirilabilir sinir tabaka icin x displaystyle x ve y displaystyle y yerine bagimsiz degiskenler olarak x displaystyle x ve u displaystyle u yu alan ve u displaystyle u yerine bagimli degisken t m u y displaystyle tau mu partial u partial y yi kayma gerilmesi kullanan bir donusum tanitti Sinir tabaka denklemi o zaman su hale gelir mru x 1t 2t u2 mdpdx u 1t 0 eger dpdx 0 ise mrt2 t x 1u 2t u2 displaystyle begin aligned amp mu rho u frac partial partial x left frac 1 tau right frac partial 2 tau partial u 2 mu frac dp dx frac partial partial u left frac 1 tau right 0 5pt amp text eger frac dp dx 0 text ise frac mu rho tau 2 frac partial tau partial x frac 1 u frac partial 2 tau partial u 2 end aligned Orijinal koordinat suradan geri elde edilir y m dut displaystyle y mu int frac du tau Turbulansli sinir tabakalar span Turbulansli sinir tabakalarin ele alinmasi akis ozelliklerinin zamana bagli degisimi nedeniyle cok daha zordur Turbulansli akislarin ele alinmasinda en yaygin kullanilan tekniklerden biri Reynolds decomposition uygulamaktir Burada anlik akis ozellikleri ortalama ve dalgalanan fluctuation bir bilesene ayristirilir dalgalanan bilesenin ortalamasinin her zaman sifir oldugu varsayilir Bu teknigin sinir tabaka denklemlerine uygulanmasi literaturde sikca verilmeyen tam turbulansli sinir tabaka denklemlerini verir u x v y 0 displaystyle partial overline u over partial x partial overline v over partial y 0 u u x v u y 1r p x n 2u x2 2u y2 y u v x u 2 displaystyle overline u partial overline u over partial x overline v partial overline u over partial y 1 over rho partial overline p over partial x nu left partial 2 overline u over partial x 2 partial 2 overline u over partial y 2 right frac partial partial y overline u v frac partial partial x overline u 2 u v x v v y 1r p y n 2v x2 2v y2 x u v y v 2 displaystyle overline u partial overline v over partial x overline v partial overline v over partial y 1 over rho partial overline p over partial y nu left partial 2 overline v over partial x 2 partial 2 overline v over partial y 2 right frac partial partial x overline u v frac partial partial y overline v 2 Benzer bir olcek analizi kullanilarak yukaridaki denklemler basat terimlere indirgenebilir Enine yondeki degisimler icin uzunluk olcegi d displaystyle delta ve akis yonundeki degisimler icin L displaystyle L secilerek burada d lt lt L displaystyle delta lt lt L x momentumu denklemi su sekilde basitlesir u u x v u y 1r p x n 2u y2 y u v displaystyle overline u partial overline u over partial x overline v partial overline u over partial y 1 over rho partial overline p over partial x nu partial 2 overline u over partial y 2 frac partial partial y overline u v Bu denklem duvardaki kaymazlik kosulunu saglamaz Prandtl in kendi sinir tabaka denklemleri icin yaptigi gibi viskoz terimin momentum denkleminde basat terim olmasini saglamak icin yeni daha kucuk bir uzunluk olcegi kullanilmalidir y olcegi olarak h lt lt d displaystyle eta lt lt delta secilerek bu ic sinir tabaka icin basat momentum denklemi su sekilde verilir 0 1r p x n 2u y2 y u v displaystyle 0 1 over rho partial overline p over partial x nu partial 2 overline u over partial y 2 frac partial partial y overline u v Sonsuz Reynolds sayisi limitinde basinc gradyani teriminin turbulansli sinir tabakanin ic bolgesi uzerinde hicbir etkisi olmadigi gosterilebilir Yeni ic uzunluk olcegi h displaystyle eta viskoz bir uzunluk olcegidir ve nu displaystyle frac nu u mertebesindedir burada u displaystyle u turbulans dalgalanmalarinin hiz olcegidir bu durumda bir friction velocity Laminer sinir tabaka denklemlerinin aksine farkli akis olcekleri kumeleri yani ic ve dis olcekleme tarafindan yonetilen iki rejimin varligi turbulansli sinir tabaka icin evrensel bir benzerlik cozumu bulmayi zor ve tartismali hale getirmistir Akisin her iki bolgesini de kapsayan bir benzerlik cozumu bulmak icin akisin her iki bolgesinden gelen cozumleri asimptotik olarak eslestirmek gerekir Bu tur bir analiz ya ya da kuvvet yasasini verecektir Sikistirilabilir akislarda enerji denklemi kullanilarak isil sinir tabakalar icin de benzer yaklasimlar uygulanmistir Turbulansli sinir tabaka denklemlerindeki ek terim u v displaystyle overline u v Reynolds kayma gerilmesi olarak bilinir ve a priori onsel olarak bilinmemektedir Bu nedenle turbulansli sinir tabaka denklemlerinin cozumu Reynolds kayma gerilmesini bilinen akis degiskenleri veya turevleri cinsinden ifade etmeyi amaclayan bir kullanilmasini gerektirir Bu tur modellerin dogruluk ve genellikten yoksun olmasi modern akiskanlar dinamiginde turbulansli akis ozelliklerinin basarili bir sekilde tahmin edilmesinde buyuk bir engeldir Duvar yakinindaki bolgede sabit bir gerilme tabakasi mevcuttur Dikey hiz dalgalanmalarinin duvar yakininda sonumlenmesi nedeniyle terimi ihmal edilebilir hale gelir ve dogrusal bir hiz profilinin var oldugunu buluruz Bu sadece cok duvar yakini bolge icin gecerlidir Isi ve kutle transferi span 1928 de Fransiz muhendis Andre Leveque akan bir akiskandaki konvektif isi transferinin yalnizca yuzeye cok yakin hiz degerlerinden etkilendigini gozlemledi Buyuk Prandtl sayisina sahip akislar icin yuzeyden serbest akim sicakligina sicaklik kutle gecisi yuzeye cok yakin cok ince bir bolgede gerceklesir Bu nedenle en onemli akiskan hizlari hiz degisiminin yuzeyden normal mesafeyle dogrusal kabul edilebilecegi bu cok ince bolge icindekilerdir Bu sekilde u y U 1 y h 2h2 Uyh 2 yh displaystyle u y U left 1 frac y h 2 h 2 right U frac y h left 2 frac y h right icin y 0 displaystyle y rightarrow 0 oldugunda u y 2Uyh 8y displaystyle u y approx 2U frac y h theta y burada 8 duvari kesen Poiseuille parabolunun tegetidir Leveque in cozumu bir Poiseuille akisina isi transferine ozgu olsa da icgorusu diger bilim insanlarinin isil sinir tabaka problemine kesin bir cozum bulmasina yardimci oldu Schuh bir sinir tabakada u nun yine y nin dogrusal bir fonksiyonu oldugunu ancak bu durumda duvar tegetinin x in bir fonksiyonu oldugunu gozlemledi Bunu Leveque profilinin degistirilmis bir versiyonuyla ifade etti u y 8 x y displaystyle u y theta x y Bu dusuk Pr displaystyle Pr sayilari icin bile cok iyi bir yaklasimla sonuclanir oyle ki sadece Pr displaystyle Pr sayisi 1 den cok kucuk olan sivi metaller bu sekilde ele alinamaz 1962 de Kestin ve Persen isil sinir tabakanin tamamen momentum tabakasi icinde oldugu durumlar ve cesitli duvar sicaklik dagilimlari icin isi transferi cozumlerini aciklayan bir makale yayinladilar x x0 displaystyle x x 0 da bir sicaklik sicramasi olan duz bir levha problemi icin parabolik isil sinir tabaka denklemini bir bayagi diferansiyel denkleme indirgeyen bir ikame onerdiler Bu denklemin cozumu yani akiskan icindeki herhangi bir noktadaki sicaklik eksik bir gama fonksiyonu olarak ifade edilebilir isil sinir tabaka denklemini cozumu ayni eksik gama fonksiyonu olan bir bayagi diferansiyel denkleme indirgeyen esdeger bir ikame onerdi Isi iletimini iceren sikistirilamaz sinir tabaka denklemleri icin zamana bagli self similarity ansatz tahmin yuruterek hesaplama ile analitik cozumler turetilebilir Cesitli ders kitaplarindan iyi bilindigi uzere sinir tabakanin artmasiyla isi transferi azalma egilimindedir Yakin zamanda bir fotovoltaik jeneratorden gecen ruzgarin azalan isi transferi nedeniyle turbulansli bir rejim altinda PV panellerindeki isiyi hapsetme egiliminde oldugu pratik ve buyuk olcekte gozlemlendi Siklikla dogasi geregi turbulansli oldugu varsayilmasina ragmen bu tesadufi gozlem dogal ruzgarin pratikte ideal bir akiskana cok yakin davrandigini en azindan duz bir levhadaki beklenen davranisa benzeyen bir gozlemde bu tur fenomenlerin daha buyuk olcekte analiz edilmesindeki zorlugu potansiyel olarak azalttigini gostermektedir Sinir tabaka analizinden konvektif transfer sabitleri span yukaridaki denklemleri icin kesin bir cozum turetti Sinir tabaka d displaystyle delta laminer akis icin Reynolds sayisinin bir fonksiyonudur d 5 0xRe displaystyle delta approx 5 0 x over sqrt Re d displaystyle delta sinir tabakanin kalinligi hizin uzak alan hizi v displaystyle v infty un 99 undan az oldugu akis bolgesi x displaystyle x yari sonsuz levha boyunca konum ve Re displaystyle Re ise rv x m displaystyle rho v infty x mu ile verilen Reynolds Sayisidir r displaystyle rho yogunluk ve m displaystyle mu dinamik viskozite Blasius cozumu sinir kosullarini boyutsuz bir formda kullanir vx vSv vS vxv vyv 0 displaystyle v x v S over v infty v S v x over v infty v y over v infty 0 y 0 displaystyle y 0 da vx vSv vS vxv 1 displaystyle v x v S over v infty v S v x over v infty 1 y displaystyle y infty da ve x 0 displaystyle x 0 daHiz Sinir Tabakasi Ust turuncu ve Sicaklik Sinir Tabakasi Alt yesil Momentum Enerji Dengeleri ve sinir kosullarindaki benzerlik nedeniyle islevsel bir formu paylasir Bircok durumda kaymazlik sinir kosulunun levha yuzeyindeki akiskan hizi vS displaystyle v S nin tum konumlarda levhanin hizina esit oldugunu kabul ettigine dikkat edin Eger levha hareket etmiyorsa o zaman vS 0 displaystyle v S 0 olur Akiskan kaymasina izin verilirse cok daha karmasik bir turetme gerekir Aslinda yari sonsuz bir levha uzerindeki sinir tabakadaki laminer hiz profili icin Blasius cozumu sirasiyla isi ve kutle transferi icin Isil ve Konsantrasyon sinir tabakalarini tanimlamak uzere kolayca genisletilebilir Diferansiyel x momentum dengesi hareket denklemi yerine bu benzer sekilde turetilmis Enerji ve Kutle dengesini kullanir Enerji vx T x vy T y krCp 2T y2 displaystyle v x partial T over partial x v y partial T over partial y k over rho C p partial 2 T over partial y 2 Kutle vx cA x vy cA y DAB 2cA y2 displaystyle v x partial c A over partial x v y partial c A over partial y D AB partial 2 c A over partial y 2 Momentum dengesi icin kinematik viskozite n displaystyle nu momentum difuzivitesi yayilimi olarak kabul edilebilir Enerji dengesinde bunun yerini isil difuzivite a k rCP displaystyle alpha k rho C P kutle dengesinde ise kutle difuzivitesi DAB displaystyle D AB alir Bir maddenin k displaystyle k onun isil iletkenligi r displaystyle rho yogunlugu ve CP displaystyle C P isi kapasitesidir AB indisi A turunun B turune difuzyonunu yayilimini belirtir a DAB n displaystyle alpha D AB nu varsayimi altinda bu denklemler momentum dengesine esdeger hale gelir Boylece Prandtl sayisi Pr n a 1 displaystyle Pr nu alpha 1 ve Schmidt sayisi Sc n DAB 1 displaystyle Sc nu D AB 1 icin Blasius cozumu dogrudan gecerlidir Buna gore bu turetme v displaystyle v yi T displaystyle T veya cA displaystyle c A mutlak sicaklik veya A turunun konsantrasyonu ile degistirerek sinir kosullarinin ilgili bir formunu kullanir S indisi bir yuzey kosulunu belirtir vx vSv vS T TST TS cA cAScA cAS 0 displaystyle v x v S over v infty v S T T S over T infty T S c A c AS over c A infty c AS 0 y 0 displaystyle y 0 da vx vSv vS T TST TS cA cAScA cAS 1 displaystyle v x v S over v infty v S T T S over T infty T S c A c AS over c A infty c AS 1 y displaystyle y infty da ve x 0 displaystyle x 0 da Akim cizgisi fonksiyonunu kullanarak Blasius levha yuzeyindeki kayma gerilmesi icin asagidaki cozumu elde etti t0 vx y y 0 0 332v xRe1 2 displaystyle tau 0 left partial v x over partial y right y 0 0 332 v infty over x Re 1 2 Ve sinir kosullari araciligiyla sunlar bilinmektedir vx vSv vS T TST TS cA cAScA cAS displaystyle v x v S over v infty v S T T S over T infty T S c A c AS over c A infty c AS Levha yuzeyinden disari isi kutle akisi icin asagidaki iliskiler verilir T y y 0 0 332T TSxRe1 2 displaystyle left partial T over partial y right y 0 0 332 T infty T S over x Re 1 2 cA y y 0 0 332cA cASxRe1 2 displaystyle left partial c A over partial y right y 0 0 332 c A infty c AS over x Re 1 2 Boylece Pr Sc 1 displaystyle Pr Sc 1 icin d dT dc 5 0xRe displaystyle delta delta T delta c 5 0x over sqrt Re burada dT dc displaystyle delta T delta c T displaystyle T ve cA displaystyle c A nin uzak alan degerlerinin 99 undan az oldugu akis bolgeleridir Belirli bir akiskanin Prandtl sayisi genellikle bir olmadigindan Ludwig Prandtl ile calisan Alman muhendis E Pohlhausen bu denklemleri Pr 1 displaystyle Pr neq 1 icin gecerli olacak sekilde ampirik olarak genisletmeye calisti Sonuclari Sc displaystyle Sc ye de uygulanabilir Prandtl sayisinin 0 6 dan buyuk olmasi durumunda yaklasik olarak su sekilde verildigini buldu Cesitli Prandtl Sayilari icin hiz sinir tabakasina kirmizi renkte kiyasla isil sinir tabakanin goreli kalinligini gosteren grafik Pr 1 displaystyle Pr 1 icin ikisi esittir ddT Pr1 3 displaystyle delta over delta T Pr 1 3 ve bu nedenle ddc Sc1 3 displaystyle delta over delta c Sc 1 3 Bu cozumden konvektif isi kutle transferi sabitlerini sinir tabaka akis bolgesine dayanarak karakterize etmek mumkundur Fourier iletim yasasi ve Newton un Soguma Yasasi yukarida turetilen aki terimi ve sinir tabaka kalinligi ile birlestirilir qA k T y y 0 hx TS T displaystyle q over A k left partial T over partial y right y 0 h x T S T infty hx 0 332kxRex1 2Pr1 3 displaystyle h x 0 332 k over x Re x 1 2 Pr 1 3 Bu yari sonsuz duzlem uzerindeki bir noktadaki yerel konvektif sabit hx displaystyle h x i verir Levhanin uzunlugu boyunca entegrasyon bir ortalama verir hL 0 664kxReL1 2Pr1 3 displaystyle h L 0 664 k over x Re L 1 2 Pr 1 3 Kutle transferi terimleriyle k displaystyle k konvektif kutle transferi sabiti DAB displaystyle D AB A turunun B turune difuzivitesi Sc n DAB displaystyle Sc nu D AB turetme izlendiginde asagidaki cozumler elde edilir kx 0 332DABxRex1 2Sc1 3 displaystyle k x 0 332 D AB over x Re x 1 2 Sc 1 3 kL 0 664DABxReL1 2Sc1 3 displaystyle k L 0 664 D AB over x Re L 1 2 Sc 1 3 Bu cozumler Prandtl Schmidt sayisi 0 6 dan buyuk olan laminer akis icin gecerlidir Gemi insa muhendisligi span Ucaklar icin gecerli olan prensiplerin cogu hava yerine birincil akiskan olarak suyun soz konusu oldugu gemiler denizaltilar ve acik deniz platformlari icin de gecerlidir Su ideal bir akiskan olmadigindan suda hareket eden gemiler direncle karsilasir Akiskan parcaciklari su ile gemi arasindaki yapisma kuvveti nedeniyle geminin tekne govdesine yapisir ve akis hizinin kucuk ama dik bir hiz gradyani olusturdugu bir sinir tabaka meydana getirir gemiyle temas halindeki akiskan ideal olarak 0 bagil hiza sahipken sinir tabakanin sinirindaki akiskan hizina veya akiskanin gemi etrafindaki bagil hizina sahiptir Geminin onu cevresindeki akiskan nedeniyle normal basinc kuvvetleriyle karsilasirken arka kisim sinir tabaka nedeniyle daha dusuk bir etkiyen basinc bileseni gorur Bu durum viskoz basinc suruklemesi veya form suruklemesi olarak bilinen basinc kaynakli daha yuksek bir dirence yol acar Gemiler icin ucaklarin aksine su yogunlugundaki degisimin ihmal edilebilir oldugu sikistirilamaz akislarla ilgilenilir 1000 kPa ya yakin bir basinc artisi yalnizca 2 3 kg m3 luk bir degisime yol acar Bu akiskanlar dinamigi alanina hidrodinamik denir Bir gemi muhendisi once hidrodinamik icin sonra mukavemet icin tasarim yapar Sinir tabaka gelisimi bozulmasi ve ayrilmasi kritiktir cunku suyun yuksek viskozitesi yuksek kayma gerilmeleri uretir Sinir tabaka turbini span Bu etki 1913 yilinda Nikola Tesla tarafindan patenti alinan kullanilmistir Geleneksel bir turbinde oldugu gibi kanatlara carpan bir akiskan degil sinir tabaka etkisini kullandigi icin kanatsiz turbin olarak adlandirilir Sinir tabaka turbinleri ayni zamanda kohezyon tipi turbin kanatsiz turbin ve Prandtl tabakasi turbini Ludwig Prandtl a atifla olarak da bilinir Boyut analizi kullanarak bir silindirdeki gecici sinir tabaka kalinliginin tahmini span Silindirik bir akis icin gecici ve viskoz kuvvet denklemlerini kullanarak Womersley Sayisini Nw displaystyle N w bularak gecici sinir tabaka kalinligini tahmin edebilirsiniz Gecici Kuvvet rvw displaystyle rho vw Viskoz Kuvvet mvd12 displaystyle mu v over delta 1 2 Bunlari birbirine esitlemek sunu verir rvw mvd12 displaystyle rho vw mu v over delta 1 2 Delta icin cozum d1 mrw v w displaystyle delta 1 sqrt mu over rho w sqrt v over w Boyutsuz formda Ld1 Lw v Nw displaystyle L over delta 1 L sqrt w over v N w burada Nw displaystyle N w Womersley Sayisi r displaystyle rho yogunluk v displaystyle v hiz w displaystyle w salinim frekansi d1 displaystyle delta 1 gecici sinir tabakanin uzunlugu m displaystyle mu viskozite L displaystyle L karakteristik uzunluk Boyut analizi kullanarak bir silindirdeki sinir tabakada konvektif akis kosullarinin tahmini span Silindirik bir akis icin sinir tabakadaki konvektif ve viskoz kuvvet denklemlerini kullanarak boyutsuz Reynolds Sayisini Re displaystyle Re bularak sinir tabakadaki konvektif akis kosullarini tahmin edebilirsiniz Konvektif kuvvet rv2 L displaystyle rho v 2 over L Viskoz kuvvet mvd22 displaystyle mu v over delta 2 2 Bunlari birbirine esitlemek sunu verir rv2 L mvd22 displaystyle rho v 2 over L mu v over delta 2 2 Delta icin cozum d2 mLrv displaystyle delta 2 sqrt mu L over rho v Boyutsuz formda Ld2 rvLm Re displaystyle L over delta 2 sqrt rho vL over mu sqrt Re burada Re displaystyle Re Reynolds Sayisi r displaystyle rho yogunluk v displaystyle v hiz d2 displaystyle delta 2 konvektif sinir tabakanin uzunlugu m displaystyle mu viskozite L displaystyle L karakteristik uzunluk Sinir tabaka yutulmasi span Sinir tabaka yutulmasi yavas govde sinir tabakasini yutan ve suruklemeyi azaltmak ve artirmak icin iz bolgesini yeniden enerjelendiren kica monte edilmis bir ile bir artis vaat etmektedir Bozuk hava akisinda calismak icin fan daha agirdir verimliligi azalir ve entegrasyonu zordur veya Fransiz arastirma ajansi nin Nova konsepti gibi tasarimlarda govde sinir tabakasinin 40 ini yutarak seyir sirasinda 5 tasarruf saglamak icin kullanilir Airbus Nautilius konseptini Eylul 2018 deki ICAS kongresinde sundu azimut akis bozulmasini en aza indirirken tum govde sinir tabakasini yutmak icin govde 13 18 1 fanlara sahip iki ige ayrilir Itici verimlilikleri daha kucuk daha hafif daha az karmasik ve gurultulu motorlara sahip zit yonlu donen gibi 90 a kadar cikar Normal bir kanat alti 15 1 baypas oranli motora kiyasla yakit tuketimini 10 dan fazla dusurebilir Ayrica bakiniz span Sinir tabaka ayrilmasi Perturbasyon teorisi Kayma gerilmesiKaynakca span Young A D 1989 Boundary layers 1st publ Washington DC American Institute of Aeronautics and Astronautics ISBN 0930403576 Schlichting Hermann Gersten Klaus 2017 2 1 Boundary Layer Concept Boundary Layer theory Ninth Berlin Heidelberg Springer s 29 doi 10 1007 978 3 662 52919 5 2 ISBN 978 3 662 52917 1 Erisim tarihi 5 Agustos 2023 Siklikla sinir keyfi olarak hizin dis hizin belirli bir yuzdesine ulastigi nokta olarak verilir orn 99 Aciklik icin genellikle bir indis kullanilir orn d99 Prandtl L 1938 Zur Berechnung der Grenzschichten Zeitschrift fur Angewandte Mathematik und Mechanik 18 1 ss 77 82 Bibcode 1938ZaMM 18 77P doi 10 1002 zamm 19380180111 Van Dyke Milton Perturbation methods in fluid mechanics Parabolic Press Incorporated 1975 Stewartson K 1957 On Asymptotic Expansions in the Theory of Boundary Layers Journal of Mathematics and Physics 36 1 4 ss 173 191 doi 10 1002 sapm1957361173 Libby Paul A Fox Herbert 1963 Some perturbation solutions in laminar boundary layer theory Journal of Fluid Mechanics 17 3 s 433 doi 10 1017 S0022112063001439 Fox Herbert Libby Paul A 1964 Some perturbation solutions in laminar boundary layer theory Part 2 The energy equation Journal of Fluid Mechanics 19 3 ss 433 451 Bibcode 1964JFM 19 433F doi 10 1017 S0022112064000830 von Karman T 1921 Uber laminare und turbulente Reibung Zeitschrift fur Angewandte Mathematik und Mechanik 1 4 ss 233 252 Bibcode 1921ZaMM 1 233K doi 10 1002 zamm 19210010401 Wieghardt K On an energy equation for the calculation of laminar boundary layers Joint Intelligence Objectives Agency 1946 Wieghardt K 1948 Uber einen Energiesatz zur Berechnung laminarer Grenzschichten Ingenieur Archiv 16 3 4 ss 231 242 Bibcode 1948AAM 16 231W doi 10 1007 BF00548007 Rosenhead Louis ed Laminar boundary layers Clarendon Press 1963 Tollmien Walter Schlichting Hermann Gortler Henry Riegels F W 1961 Bemerkungen zur Hydrodynamik Ludwig Prandtl Gesammelte Abhandlungen ss 627 631 doi 10 1007 978 3 662 11836 8 49 ISBN 978 3 662 11837 5 von Karman T Tsien H S 1938 Boundary Layer in Compressible Fluids Journal of the Aeronautical Sciences 5 6 ss 227 232 doi 10 2514 8 591 Crocco L A characteristic transformation of the equations of the boundary layer in gases ARC 4582 1939 1940 von Karman T 1939 The analogy between fluid friction and heat transfer Transactions of the American Society of Mechanical Engineers 61 8 ss 705 710 doi 10 1115 1 4021298 Guo J Yang X I A Ihme M March 2022 Structure of the thermal boundary layer in turbulent channel flows at transcritical conditions Journal of Fluid Mechanics Ingilizce Cilt 934 Bibcode 2022JFM 934A 45G doi 10 1017 jfm 2021 1157 ISSN 0022 1120 Leveque A 1928 Les lois de la transmission de chaleur par convection Annales des Mines ou Recueil de Memoires sur l Exploitation des Mines et sur les Sciences et les Arts qui s y Rattachent Memoires Fransizca XIII 13 ss 201 239 a b Niall McMahon Andre Leveque p285 a review of his velocity profile approximation 4 Haziran 2012 tarihinde kaynagindan arsivlendi a b Martin H 2002 The generalized Leveque equation and its practical use for the prediction of heat and mass transfer rates from pressure drop Chemical Engineering Science 57 16 ss 3217 3223 Bibcode 2002ChEnS 57 3217M doi 10 1016 S0009 2509 02 00194 X Schuh H 1953 On Asymptotic Solutions for the Heat Transfer at Varying Wall Temperatures in a Laminar Boundary Layer with Hartree s Velocity Profiles Journal of the Aeronautical Sciences 20 2 ss 146 147 doi 10 2514 8 2566 Kestin J Persen L N 1962 The transfer of heat across a turbulent boundary layer at very high prandtl numbers International Journal of Heat and Mass Transfer 5 5 ss 355 371 Bibcode 1962IJHMT 5 355K doi 10 1016 0017 9310 62 90026 1 Schlichting H 1979 Boundary Layer Theory 7 New York USA McGraw Hill Barna Imre Ferenc Bognar Gabriella Matyas Laszlo Hriczo Krisztian 2022 Self similar analysis of the time dependent compressible and incompressible boundary layers including heat conduction Journal of Thermal Analysis and Calorimetry Cilt 147 ss 13625 13632 arXiv 2101 08990 doi 10 1007 s10973 022 11574 3 Rossa Carlos 2023 Energy losses in photovoltaic generators due to wind patterns Nature Communications Engineering 2 66 Bibcode 2023CmEng 2 66R doi 10 1038 s44172 023 00119 7 PMC 10956078 Blasius H 1908 Grenzschichten in Flussigkeiten mit kleiner Reibung Zeitschrift fur Mathematik und Physik Cilt 56 ss 1 37 Ingilizce ceviri Martin Michael J 2001 Blasius boundary layer solution with slip flow conditions AIP Conference Proceedings 585 ss 518 523 doi 10 1063 1 1407604 hdl 2027 42 87372 a b Geankoplis Christie J Transport Processes and Separation Process Principles includes Unit Operations Fourth ed Upper Saddle River NJ Prentice Hall Professional Technical Reference 2003 Print Pohlhausen E 1921 Der Warmeaustausch zwischen festen Korpern und Flussigkeiten mit kleiner reibung und kleiner Warmeleitung Zeitschrift fur Angewandte Mathematik und Mechanik 1 2 ss 115 121 Bibcode 1921ZaMM 1 115P doi 10 1002 zamm 19210010205 a b Resistance and Powering of Ships PDF usna edu Erisim tarihi 14 Subat 2024 Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddeler link a b c Graham Warwick 19 Kasim 2018 The Week In Technology November 19 23 2018 Aviation Week amp Space Technology 2009 Applied Hydrodynamics An Introduction to Ideal and Real Fluid Flows CRC Press Taylor amp Francis Group Leiden The Netherlands 478 pages ISBN 978 0 415 49271 3 A D Polyanin and V F Zaitsev Handbook of Nonlinear Partial Differential Equations Chapman amp Hall CRC Press Boca Raton London 2004 1 58488 355 3 A D Polyanin A M Kutepov A V Vyazmin and D A Kazenin Hydrodynamics Mass and Heat Transfer in Chemical Engineering Taylor amp Francis London 2002 0 415 27237 8 Hermann Schlichting Klaus Gersten E Krause H Jr Oertel C Mayes Boundary Layer Theory 8th edition Springer 2004 3 540 66270 7 John D Anderson Jr Ludwig Prandtl s Boundary Layer Physics Today December 2005 Anderson John 1992 Fundamentals of Aerodynamics 2nd Toronto S S CHAND ss 711 714 ISBN 0 07 001679 8 and A First Course in Turbulence The MIT Press 1972 Lectures in Turbulence for the 21st Century by William K GeorgeDis baglantilar span National Science Digital Library Boundary Layer Moore Franklin K Displacement effect of a three dimensional boundary layer NACA Report 1124 1953 Benson Tom Boundary layer NASA Glenn Learning Technologies Boundary layer separation Boundary layer equations Exact Solutions from EqWorld Jones T V BOUNDARY LAYER HEAT TRANSFER The revolutionary concept of boundary layer and its prevalence in aeronautics by Sourabh S Diwan YouTube International Centre for Theoretical Sciences 18 Subat 2022 Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddeler link Otorite kontroluNDL 00567209 NKC ph139001 NLI 987007283990105171 Kategoriler Sinir tabakalarUcak kanadi tasarimiIsi transferiGizli kategoriler Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddelerNDL tanimlayicisi olan Vikipedi maddeleriNKC tanimlayicisi olan Vikipedi maddeleriNLI tanimlayicisi olan Vikipedi maddeleri
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State







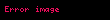



























![{\displaystyle {\begin{aligned}&\mu \rho u{\frac {\partial }{\partial x}}\left({\frac {1}{\tau }}\right)+{\frac {\partial ^{2}\tau }{\partial u^{2}}}-\mu {\frac {dp}{dx}}{\frac {\partial }{\partial u}}\left({\frac {1}{\tau }}\right)=0,\\[5pt]&{\text{eğer }}{\frac {dp}{dx}}=0,{\text{ ise }}{\frac {\mu \rho }{\tau ^{2}}}{\frac {\partial \tau }{\partial x}}={\frac {1}{u}}{\frac {\partial ^{2}\tau }{\partial u^{2}}}.\end{aligned}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eE1XSXlZakV3Tm1JME1Ea3pPR1ppTWpCbVlXRmhOekkzWm1VME9HVmxaRGhqWTJZelptUTIuc3Zn.svg)




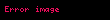









![{\displaystyle u(y)=U\left[1-{\frac {(y-h)^{2}}{h^{2}}}\right]=U{\frac {y}{h}}\left[2-{\frac {y}{h}}\right]\;,}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4NE1qTm1PR1kzTldZMU4yTm1aR0k1WWpRMk5UY3laVFEyWVRSbU5XSXdOR1ZpWmprM1pUQXcuc3Zn.svg)































































