Bu madde önerilmeyen biçimde kaynaklandırılmıştır. () |
Navier-Stokes denklemleri, ismini Claude-Louis Navier ve George Gabriel Stokes'tan almış olan, sıvılar ve gazlar gibi akışkanların hareketini tanımlamaya yarayan bir dizi denklemden oluşmaktadır.

Bu denklemler; akışkan içerisindeki birim kütleye etki eden momentum (ivmelenme) değişimlerinin, basınç değişimleri ve sürtünme kayıplarına neden olan viskoz kuvvetlerin (sürtünmeye benzer) toplamına eşit olduğunun doğruluğunu ortaya koymaktadır. Bu viskoz kuvvetler moleküller arası etkileşimlerden meydana gelmekte ve akışkanın akmaya ne kadar dirençli (viskoz) olduğunu göstermektedir. Böylece, Navier-Stokes denklemlerinin, verilen akışkanın herhangi bir bölgesindeki kuvvetler dengesinin dinamik ifadesi olduğu söylenebilir.
Bu denklemler en kullanışlı denklemlerin başında gelmektedirler. Çünkü, gerek akademik gerekse ekonomik birçok fenomenin fiziğini açıklamaktadır. Hava akımları ve okyanus akıntılarının, boru içindeki su akışının, galaksideki yıldız hareketlerinin, kanat etrafındaki hava akımlarının modellenmesinde ve hesaplarında sıkça kullanılırlar.
Temel kabuller
Navier-Stokes denklemlerinin detayına girmeden önce, akışkanlar hakkında bazı kabuller yapılması gereklidir. Öncelikle akışkanın sürekli olduğu kabul edilir. Yani akışkanın tamamının aynı özellikte olduğu içinde farklı biçimler (formlar) bulunmadığı kabul edilir. Bir başka gerekli kabul de konu ile ilgili tüm alanların basınç, hız, yoğunluk, sıcaklık vs., diferansiyel olduğudur. (faz değişimleri olmadan)
Denklemler, momentum ve enerji ve temel prensiplerinden elde edilir. Bunun için, bazı hallerde kontrol hacmi adı verilen, rastgele seçilmiş sonlu bir hacim belirlemek gereklidir, bu hacim üzerinde bu prensipler kolayca uygulanabilir. Bu sonlu hacim 

Gerçek türev
Hareket eden akışkanın özelliklerinin değişiminin ölçülebilmesi için iki yol vardır. Örneğin dünya atmosferindeki rüzgar hızının değişimleri ele alınacak olursa; bu değişiklikler bir meteoroloji istasyonu ölçüm cihazı (anemometre) veya bir hava balonu yolu ile ölçülebilir. Şüphesiz, ilk durumdaki anemometre boşlukta sabit bir nokta boyunca geçiş yapan tüm hareketli parçacıkların hızını ölçerken, ikinci durumda bahsedilen aygıt akışkan ile beraber hareket ederken hızdaki değişimi ölçer.
Aynı durumda, yoğunluk, sıcaklık vb. değişimler de ölçümü etkileyecektir. Bu nedenle, bu iki hal için bir ayrım yapılmalıdır. Bir alanın boşluktaki sabit bir pozisyona göre türevi uzaysal (spatial) veya Euleryen türev (Eulerian derivative) olarak adlandırılır. Hareketli bir parçacığın izlenmesi türevi gerçek (substantive), Lagrangyan (Lagrangian) veya maddi (material) türev olarak adlandırılır.
Gerçek türev şu şekilde tanımlanır:
Burada 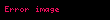
Korunum kanunları
Navier-Stokes denklemleri, aşağıdaki korunum kanunlarından türetilir:
Ek olarak, akışkan için bir durum denklemi bağıntısı kabulü yapılması gereklidir.
En genel biçimde, bir korunum kanunu şunu ifade eder, bir kontrol hacmi üzerinde tanımlanmış hacim özelliği (bulk property) değişiminin oranı 
Bu denklemde v akışkanın hızı ve 
Eğer kontrol hacmi boşluk içinde sabitlenmiş ise bu integral denkleminden aşağıdaki şekilde bir ifade yazılabilir.
Ayrıca, kontrol hacminin içinde, bu son denklemde elde edilmiş olan sağ taraftaki ilk terimin ifade edilmesi için diverjans teoremi kullanılmıştır. Böylece:
Yukarıdaki ifade boşlukta sabit kalan bir kontrol hacminde 


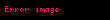
Gerçek türev, 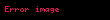
Süreklilik denklemi
Kütlenin korunumu şu şekilde yazılır:
Burada 
Sıkıştırılamaz bir akışkan için 
Momentumun korunumu
Momentumun korunumu, yoğunluk yerine momentumun vektör bileşenleri ve akışkan üzerine etkiyen kuvvetler ile, süreklilik denklemine benzer bir yaklaşım yapılarak ifade edilir. Süreklilik denkleminde 


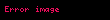

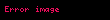
Ayrıca, 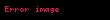
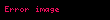
Süreklilik denkleminin kullanımı daha da basitleştirilebilir ve şu hale gelir:
Genel kullanımda aşağıdaki gibi de yazılabilir.
Bu bağlamda F=ma ifadesi doğrulanmış olur.
Denklemler
Genel biçim
Denklemlerin elde edilişi
Momentumun korunumu için Navier-Stokes denklemlerinin genel biçimi :
Burada 


Burada 


Sonuç olarak:
Burada 

Bu denklemler hala tamamlanmamıştır. Tamamlamak için, 
Akış, sürekli ve diferansiyel kabul edilmiş ve korunum kanunları çerçevesinde kısmi diferansiyel denklemler ile ifade edilmiştir. Akışın sıkıştırılamaz (sabit yoğunluk) olduğu durumda, değişkenler, basınç ve hız bileşenleri için çözülmüştür. Bu değişkenler, Navier-Stokes denklemlerinin üç bileşeni, kütlenin korunumu (süreklilik denklemi) ilave edilerek, kapalı bir sistem için kısmi diferansiyel denklemler ile, sınır şartlarına uygun olarak çözülebilir. Sıkıştırılamaz akış durumunda, yoğunluk sistem için diğer bir bilinmeyen haline gelir, sistem için bir durum denklemi ilavesi ile saptanır. Durum denkleminde genelde akışkanın sıcaklığı işin içine girer, o yüzden denklem enerjinin korunumu için de mutlaka çözülmelidir. Bu denklemler non-lineer'dir (yani lineer değildir) ve kapalı formdaki analitik çözümleri sadece çok basit sınır şartları için bilinir.
Denklemler, akım ve girdap fonksiyonu ikinci değişkenleri için dönüştürülebilirdir. Çözüm akışkan özelliklerine (viskozite, özgül ısı ve ısıl iletkenlik gibi) ve çalışma alanındaki sınır şartlarına bağlıdır.
Denklemlerin özel formları
Denklem akışkanlarla ilgili problemlerin çözümü için, genel bazı durumlar için sadeleştirilip, genelleştirilerek kullanılabilir.
Newtonyen (Newtonian) akışkanlar
Burada
akışkanın vizkozitesidir.
ise Kronecker delta olarak adlandırılan matematik işlemini ifade eder.(1 için i=j; 0 için i
j).
Buradan denklemi türetebilmek için, öncelikle denge hali ifade edilir, pij=-pδij. Newtonyen bir akışkan için, bu denge değerinden gerilim tensörünün sapması, hızın gradyeni içinde lineerdir. Galile sabiti () nedeni ile açık şekilde hız üzerinde bağımlı değildir. Diğer bir ifade ile, pij+pδij, 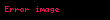
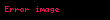
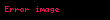


μ ve μB bazı katsayılardır. μ (shear viscosity) ve μB (bulk viscosity) olarak adlandırılır. Bu ampirik (deneysel) bir incelemedir, hacim vizkozitesi çoğu akışkan için ihmal edilebilirdir, bu nedenle çoğu zaman ihmal edilir.
Denklem içinde −2/3 ile çarpım görünmesi bununla açıklanır. Bu çarpım, 1 veya 2 uzaysal boyut içinde değiştirilebilir.
Burada, Einstein notasyonu kullanılmıştır.
Tamamı için yazıldığında, bu karmaşık denklem şu hali alır:
Momentumun korunumu:
Kütlenin korunumu:
Yoğunluk bilinmediği zaman, diğer bir denklem gereklidir.
Enerjinin korunumu:
Burada:

İdeal gaz kabul edilir:
Altı bilinmeyen (u, v, w, T, e and 
Bingham akışkanları
Bingham akışkanlarında, bazı yerlerde durum biraz daha farklıdır:
Bunlar, akış başlamadan önce bir miktar kesme dayanım kabiliyetleri olan akışkanlardır. Örnek olarak, diş macunu verilebilir.
Power-law Akışkanı (Power-law fluid)
Bu akışkan, kesme gerilimi için, ideal hal almış akışkandır, 
Bu form, hemen hemen genel akışkanların tüm çeşitlerine uygulanır.
Sıkıştırılamaz akışkanlar
Navier-Stokes denklemleri,
momentumun korunumu ve
kütlenin korunumu için
Burada
Eğer, 
(Eğer 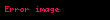
Ek olarak, eğer 
Süreklilik denklemi (sıkıştırılamazlık kabulü ile):
Silindirik koordinatlar
Navier-Stokes Süreklilik denklemi silindirik koordinatlar için şöyledir:
=0
Silindirik koordinatlar için Navier-Stokes denklemleri de şu şekilde yazılır:
r momentum:

z momentum:
Şunu ifade etmek gerekir ki, Navier-Stokes denklemleri akışkan akışını sadece yaklaşık olarak tanımlayabilir ve çok küçük ölçeklerde veya sıra dışı şartlarda, gerçek akışkanlar diğer maddeleri ve molekülleri içeren karışımlardır, Navier-Stokes denklemleri ile homojen ve sürekli akışlar modellenmiş ve bunun üzerinden sonuçlar elde edilmiştir. Bununla beraber Navier-Stokes denklemleri pratikteki problemlerin çözümü için, geniş bir aralıkta faydalı olur.
Ayrıca bakınız
Kaynakça
- İngilizce Wikipedia Navier-Stokes denklemleri maddesi 13 Eylül 2006 tarihinde Wayback Machine sitesinde arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde onerilmeyen bicimde kaynaklandirilmistir Gosterilen kaynaklar kaynak gosterme sablonlari kullanilarak dipnot belirtme bicemine uygun olarak duzenlenmelidir Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Navier Stokes denklemleri ismini Claude Louis Navier ve George Gabriel Stokes tan almis olan sivilar ve gazlar gibi akiskanlarin hareketini tanimlamaya yarayan bir dizi denklemden olusmaktadir George Gabriel Stokes Bu denklemler akiskan icerisindeki birim kutleye etki eden momentum ivmelenme degisimlerinin basinc degisimleri ve surtunme kayiplarina neden olan viskoz kuvvetlerin surtunmeye benzer toplamina esit oldugunun dogrulugunu ortaya koymaktadir Bu viskoz kuvvetler molekuller arasi etkilesimlerden meydana gelmekte ve akiskanin akmaya ne kadar direncli viskoz oldugunu gostermektedir Boylece Navier Stokes denklemlerinin verilen akiskanin herhangi bir bolgesindeki kuvvetler dengesinin dinamik ifadesi oldugu soylenebilir Bu denklemler en kullanisli denklemlerin basinda gelmektedirler Cunku gerek akademik gerekse ekonomik bircok fenomenin fizigini aciklamaktadir Hava akimlari ve okyanus akintilarinin boru icindeki su akisinin galaksideki yildiz hareketlerinin kanat etrafindaki hava akimlarinin modellenmesinde ve hesaplarinda sikca kullanilirlar Temel kabullerNavier Stokes denklemlerinin detayina girmeden once akiskanlar hakkinda bazi kabuller yapilmasi gereklidir Oncelikle akiskanin surekli oldugu kabul edilir Yani akiskanin tamaminin ayni ozellikte oldugu icinde farkli bicimler formlar bulunmadigi kabul edilir Bir baska gerekli kabul de konu ile ilgili tum alanlarin basinc hiz yogunluk sicaklik vs diferansiyel oldugudur faz degisimleri olmadan Denklemler momentum ve enerji ve temel prensiplerinden elde edilir Bunun icin bazi hallerde kontrol hacmi adi verilen rastgele secilmis sonlu bir hacim belirlemek gereklidir bu hacim uzerinde bu prensipler kolayca uygulanabilir Bu sonlu hacim W displaystyle Omega ile gosterilir ve yuzeyi sinirlandirilir W displaystyle partial Omega Kontrol hacmi sabit kalabilir veya akiskan ile hareket edebilir Temel kabuller bunlardir bununla beraber farkli uygulamalarda ozel kabuller de yapilabilir Gercek turevHareket eden akiskanin ozelliklerinin degisiminin olculebilmesi icin iki yol vardir Ornegin dunya atmosferindeki ruzgar hizinin degisimleri ele alinacak olursa bu degisiklikler bir meteoroloji istasyonu olcum cihazi anemometre veya bir hava balonu yolu ile olculebilir Suphesiz ilk durumdaki anemometre boslukta sabit bir nokta boyunca gecis yapan tum hareketli parcaciklarin hizini olcerken ikinci durumda bahsedilen aygit akiskan ile beraber hareket ederken hizdaki degisimi olcer Ayni durumda yogunluk sicaklik vb degisimler de olcumu etkileyecektir Bu nedenle bu iki hal icin bir ayrim yapilmalidir Bir alanin bosluktaki sabit bir pozisyona gore turevi uzaysal spatial veya Euleryen turev Eulerian derivative olarak adlandirilir Hareketli bir parcacigin izlenmesi turevi gercek substantive Lagrangyan Lagrangian veya maddi material turev olarak adlandirilir Gercek turev su sekilde tanimlanir DDt t v displaystyle frac D Dt star equiv frac partial star partial t mathbf v cdot nabla star Burada v displaystyle mathbf v akiskanin hizidir Denklemin sag tarafindaki ilk terim alisilmis Euleryen turevi sabit bir referans uzerindeki turev iken ikinci terim akiskan hareketi ile olusan degisiklikleri ifade eder Bu etki adveksiyon olarak adlandirilir Korunum kanunlariNavier Stokes denklemleri asagidaki korunum kanunlarindan turetilir Kutle Enerji Momentum Acisal momentum Ek olarak akiskan icin bir durum denklemi bagintisi kabulu yapilmasi gereklidir En genel bicimde bir korunum kanunu sunu ifade eder bir kontrol hacmi uzerinde tanimlanmis hacim ozelligi bulk property degisiminin orani L displaystyle L hacim sinirlari boyunca hareket eden akiskanin disari tasidigi kayip ve arti kontrol hacminin ic tarafindaki kazanclar ve kayiplara esit kabul edilir Bu asagidaki integral denklemi ile ifade edilir ddt WLdW WLv nd W WQdW displaystyle frac d dt int Omega L d Omega int partial Omega L mathbf v cdot n d partial Omega int Omega Qd Omega Bu denklemde v akiskanin hizi ve Q displaystyle Q akiskan icindeki kazanclar ve kayiplar olarak ifade edilir Eger kontrol hacmi bosluk icinde sabitlenmis ise bu integral denkleminden asagidaki sekilde bir ifade yazilabilir ddt WLdW W Lv dW WQdW displaystyle frac d dt int Omega Ld Omega int Omega nabla cdot L mathbf v d Omega int Omega Qd Omega Ayrica kontrol hacminin icinde bu son denklemde elde edilmis olan sag taraftaki ilk terimin ifade edilmesi icin diverjans teoremi kullanilmistir Boylece ddt WLdW W Lv Q dW displaystyle frac d dt int Omega Ld Omega int Omega nabla cdot L mathbf v Q d Omega Yukaridaki ifade boslukta sabit kalan bir kontrol hacminde W displaystyle Omega icin gecerlidir Cunku W displaystyle Omega zaman icinde sabittir degismez Bu sayede ddt displaystyle frac d dt ve WdW displaystyle int Omega d Omega ifadeleri birbirinin yerine yazilabilir Boylece ifade tum alanlar icin gecerli olur ve integral cikartilabilir Gercek turev Q 0 displaystyle Q 0 oldugunda kazanc ve kayip yokken elde edilir tL Lv DDtL L v 0 displaystyle frac partial partial t L nabla cdot left L mathbf v right frac D Dt L L left nabla cdot mathbf v right 0 Sureklilik denklemi Kutlenin korunumu su sekilde yazilir r t rv 0 displaystyle frac partial rho partial t nabla cdot left rho mathbf v right 0 r t r v v r displaystyle frac partial rho partial t rho nabla cdot mathbf v mathbf v cdot nabla rho DrDt r v 0 displaystyle frac D rho Dt rho nabla cdot mathbf v 0 Burada r displaystyle rho kutle yogunlugu birim hacim basina kutle v akiskanin hizidir Sikistirilamaz bir akiskan icin r displaystyle rho akis hatti boyunca degismez ve denklem su hale indirgenir v 0 displaystyle nabla cdot mathbf v 0 Momentumun korunumu Momentumun korunumu yogunluk yerine momentumun vektor bilesenleri ve akiskan uzerine etkiyen kuvvetler ile sureklilik denklemine benzer bir yaklasim yapilarak ifade edilir Sureklilik denkleminde r displaystyle rho yerine belirli bir yonde birim hacim basina net momentum yazilir rvi displaystyle rho v i burada vi displaystyle v i hizin ith displaystyle i th bilesenidir hiz x y veya z yonleri boyunca olmak uzere t rvi rviv rfi displaystyle frac partial partial t left rho v i right nabla cdot rho v i mathbf v rho f i rfi displaystyle rho f i akiskan uzerine etkiyen kuvvetin ith displaystyle i th bilesenidir her birim hacim basina gercek kuvvet Genel kuvvetler yercekimi ve basinc gradyenlerini kapsar Bu su sekilde de ifade edilebilir t rv rv v rf displaystyle frac partial partial t left rho mathbf v right nabla cdot rho mathbf v otimes mathbf v rho mathbf f Ayrica v v displaystyle mathbf v otimes mathbf v bir tensor dur displaystyle otimes tensor carpimini ifade eder Sureklilik denkleminin kullanimi daha da basitlestirilebilir ve su hale gelir rDviDt rfi displaystyle rho frac Dv i Dt rho f i Genel kullanimda asagidaki gibi de yazilabilir rDvDt rf displaystyle rho frac D mathbf v Dt rho mathbf f Bu baglamda F ma ifadesi dogrulanmis olur DenklemlerGenel bicim Denklemlerin elde edilisi Momentumun korunumu icin Navier Stokes denklemlerinin genel bicimi rDvDt P rf displaystyle rho frac D mathbf v Dt nabla cdot mathbb P rho mathbf f Burada r displaystyle rho akiskan yogunlugu v hiz vektoru ve f kitle kuvvet vektorudur P displaystyle mathbb P tensoru akiskan parcacigi uzerine uygulanmis yuzey kuvvetleri olarak tanimlanir gerilme tensoru Akiskan girdap gibi bagimsiz bir egme bukme hareketi yapmadikca P displaystyle mathbb P simetrik bir tensordur Genel olarak bicim P sxxtxytxztyxsyytyztzxtzyszz p000p000p sxx ptxytxztyxsyy ptyztzxtzyszz p displaystyle mathbb P begin pmatrix sigma xx amp tau xy amp tau xz tau yx amp sigma yy amp tau yz tau zx amp tau zy amp sigma zz end pmatrix begin pmatrix p amp 0 amp 0 0 amp p amp 0 0 amp 0 amp p end pmatrix begin pmatrix sigma xx p amp tau xy amp tau xz tau yx amp sigma yy p amp tau yz tau zx amp tau zy amp sigma zz p end pmatrix Burada s displaystyle sigma normal gerilmeler t displaystyle tau tegetsel gerilmeler kesme gerilmeleri ve p gerilme tensorunun izotropik parcasi ile birlestirilmis statik basinctir sxx syy szz displaystyle sigma xx sigma yy sigma zz matris izi Ing trace akiskanin dengede olup olmadigi mutlaka tanimlanmasi hacim vizkozitesi bulk viscosity olmadikca ile daima 3p dir Sonuc olarak rDvDt p T rf displaystyle rho frac D mathbf v Dt nabla p nabla cdot mathbb T rho mathbf f Burada T displaystyle mathbb T P displaystyle mathbb P nin izsiz traceless parcasidir Bu denklemler hala tamamlanmamistir Tamamlamak icin P displaystyle mathbb P nin sekli uzerinde bir varsayim yapilmalidir soyle ki gerilme tensoru icin asagida gosterildigi gibi bir sureklilik kanununa ihtiyac vardir Akis surekli ve diferansiyel kabul edilmis ve korunum kanunlari cercevesinde kismi diferansiyel denklemler ile ifade edilmistir Akisin sikistirilamaz sabit yogunluk oldugu durumda degiskenler basinc ve hiz bilesenleri icin cozulmustur Bu degiskenler Navier Stokes denklemlerinin uc bileseni kutlenin korunumu sureklilik denklemi ilave edilerek kapali bir sistem icin kismi diferansiyel denklemler ile sinir sartlarina uygun olarak cozulebilir Sikistirilamaz akis durumunda yogunluk sistem icin diger bir bilinmeyen haline gelir sistem icin bir durum denklemi ilavesi ile saptanir Durum denkleminde genelde akiskanin sicakligi isin icine girer o yuzden denklem enerjinin korunumu icin de mutlaka cozulmelidir Bu denklemler non lineer dir yani lineer degildir ve kapali formdaki analitik cozumleri sadece cok basit sinir sartlari icin bilinir Denklemler akim ve girdap fonksiyonu ikinci degiskenleri icin donusturulebilirdir Cozum akiskan ozelliklerine viskozite ozgul isi ve isil iletkenlik gibi ve calisma alanindaki sinir sartlarina baglidir Denklemlerin ozel formlariDenklem akiskanlarla ilgili problemlerin cozumu icin genel bazi durumlar icin sadelestirilip genellestirilerek kullanilabilir Newtonyen Newtonian akiskanlar Burada m displaystyle mu akiskanin vizkozitesidir dij displaystyle delta ij ise Kronecker delta olarak adlandirilan matematik islemini ifade eder 1 icin i j 0 icin i displaystyle neq j Buradan denklemi turetebilmek icin oncelikle denge hali ifade edilir pij pdij Newtonyen bir akiskan icin bu denge degerinden gerilim tensorunun sapmasi hizin gradyeni icinde lineerdir Galile sabiti nedeni ile acik sekilde hiz uzerinde bagimli degildir Diger bir ifade ile pij pdij ivj displaystyle partial i v j de lineerdir Akiskanlarin donme sabiti belirlenir sivi kristal liquid crystal olmayanlar pij pdij izli ve izsiz simetrik tensorlerine ayrilir Benzer olarak ivj displaystyle partial i v j izli izsiz simetrik ve antisimetrik tensorlere ayrilir Antisimetrik parca sifira gider izli parca ve izsiz simetrik parcaya uygun iki katsayi vardir ivj displaystyle partial i v j nin izsiz simetrik parcasi ivj jvi 2ddij kvk displaystyle partial i v j partial j v i frac 2 d delta ij partial k v k dir burada d uzaysal olcu sayisidir ve izli parca dij kvk displaystyle delta ij partial k v k dir Bu nedenle en genel lineer donme sabiti su sekilde verilir pij pdij m ivj jvi 2ddij v mBdij v displaystyle p ij p delta ij mu left partial i v j partial j v i frac 2 d delta ij nabla cdot mathbf v right mu B delta ij nabla cdot mathbf v m ve mB bazi katsayilardir m shear viscosity ve mB bulk viscosity olarak adlandirilir Bu ampirik deneysel bir incelemedir hacim vizkozitesi cogu akiskan icin ihmal edilebilirdir bu nedenle cogu zaman ihmal edilir Denklem icinde 2 3 ile carpim gorunmesi bununla aciklanir Bu carpim 1 veya 2 uzaysal boyut icinde degistirilebilir r v t v v rf p m 2v 13 v displaystyle rho left frac partial mathbf v partial t mathbf v cdot nabla mathbf v right rho mathbf f nabla p mu left nabla 2 mathbf v frac 1 3 nabla left nabla cdot mathbf v right right r vi t vj vi xj rfi p xi m 2vi xj xj 13 2vj xi xj displaystyle rho left frac partial v i partial t v j frac partial v i partial x j right rho f i frac partial p partial x i mu left frac partial 2 v i partial x j partial x j frac 1 3 frac partial 2 v j partial x i partial x j right Burada Einstein notasyonu kullanilmistir Tamami icin yazildiginda bu karmasik denklem su hali alir Momentumun korunumu r u t u u x v u y w u z kx p x x m 2 u x 23 v y m u y v x z m w x u z displaystyle rho cdot left partial u over partial t u partial u over partial x v partial u over partial y w partial u over partial z right k x partial p over partial x partial over partial x left mu cdot left 2 cdot partial u over partial x frac 2 3 cdot nabla cdot mathbf v right right partial over partial y left mu cdot left partial u over partial y partial v over partial x right right partial over partial z left mu cdot left partial w over partial x partial u over partial z right right r v t u v x v v y w v z ky p y y m 2 v y 23 v z m v z w y x m u y v x displaystyle rho cdot left partial v over partial t u partial v over partial x v partial v over partial y w partial v over partial z right k y partial p over partial y partial over partial y left mu cdot left 2 cdot partial v over partial y frac 2 3 cdot nabla cdot mathbf v right right partial over partial z left mu cdot left partial v over partial z partial w over partial y right right partial over partial x left mu cdot left partial u over partial y partial v over partial x right right r w t u w x v w y w w z kz p z z m 2 w z 23 v x m w x u z y m v z w y displaystyle rho cdot left partial w over partial t u partial w over partial x v partial w over partial y w partial w over partial z right k z partial p over partial z partial over partial z left mu cdot left 2 cdot partial w over partial z frac 2 3 cdot nabla cdot mathbf v right right partial over partial x left mu cdot left partial w over partial x partial u over partial z right right partial over partial y left mu cdot left partial v over partial z partial w over partial y right right Kutlenin korunumu r t r u x r v y r w z 0 displaystyle partial rho over partial t partial rho cdot u over partial x partial rho cdot v over partial y partial rho cdot w over partial z 0 Yogunluk bilinmedigi zaman diger bir denklem gereklidir Enerjinin korunumu r e t u e x v e y w e z x l T x y l T y z l T z p v k v r q s m F displaystyle rho left partial e over partial t u partial e over partial x v partial e over partial y w partial e over partial z right left partial over partial x left lambda cdot partial T over partial x right partial over partial y left lambda cdot partial T over partial y right partial over partial z left lambda cdot partial T over partial z right right p cdot left nabla cdot mathbf v right mathbf k cdot mathbf v rho cdot dot q s mu cdot Phi Burada F 2 u x 2 v y 2 w z 2 v x u y 2 w y v z 2 u z w x 2 23 u x v y w z 2 displaystyle Phi 2 cdot left left partial u over partial x right 2 left partial v over partial y right 2 left partial w over partial z right 2 right left partial v over partial x partial u over partial y right 2 left partial w over partial y partial v over partial z right 2 left partial u over partial z partial w over partial x right 2 frac 2 3 cdot left partial u over partial x partial v over partial y partial w over partial z right 2 F displaystyle Phi yuksek supersonik ve hipersonik ucuslar gibi sira disi ornekler haric cogunlukla ihmal edilebilirdir Ideal gaz kabul edilir e cp T pr displaystyle e c p cdot T frac p rho Alti bilinmeyen u v w T e and r displaystyle rho ve alti denklemden olusan yukaridaki gibi bir cozum sistemi elde edilmis olur Bingham akiskanlari Bingham akiskanlarinda bazi yerlerde durum biraz daha farklidir tij t0 m vi xj vi xj gt 0 displaystyle tau ij tau 0 mu frac partial v i partial x j frac partial v i partial x j gt 0 Bunlar akis baslamadan once bir miktar kesme dayanim kabiliyetleri olan akiskanlardir Ornek olarak dis macunu verilebilir Power law Akiskani Power law fluid Bu akiskan kesme gerilimi icin ideal hal almis akiskandir t displaystyle tau su sekilde verilir t K u y n displaystyle tau K left frac partial u partial y right n Bu form hemen hemen genel akiskanlarin tum cesitlerine uygulanir Sikistirilamaz akiskanlar Navier Stokes denklemleri rDuiDt rfi p xi xj 2m eij Ddij3 displaystyle rho frac Du i Dt rho f i frac partial p partial x i frac partial partial x j left 2 mu left e ij frac Delta delta ij 3 right right momentumun korunumu ve v 0 displaystyle nabla cdot mathbf v 0 kutlenin korunumu icin Burada r displaystyle rho yogunluk ui displaystyle u i i 1 2 3 displaystyle i 1 2 3 hizin uc bileseni fi displaystyle f i govde kuvvetleri yercekimi gibi p displaystyle p basinc m displaystyle mu akiskanin o noktadaki eij 12 ui xj uj xi displaystyle e ij frac 1 2 left frac partial u i partial x j frac partial u j partial x i right D eii displaystyle Delta e ii diverjans dij displaystyle delta ij Kronecker delta Eger m displaystyle mu akiskan uzerinde esit dagilmis ise momentum denklemi uzerinde su basitlestirmeler yapilir rDuiDt rfi p xi m 2ui xj xj 13 D xi displaystyle rho frac Du i Dt rho f i frac partial p partial x i mu left frac partial 2 u i partial x j partial x j frac 1 3 frac partial Delta partial x i right Eger m 0 displaystyle mu 0 fakat akiskan sikistirilabilir ise sonucta olarak bilinen denklemler elde edilir burada onemli olan sikistirilabilir akis ve akis icindeki sok dalgalaridir Ek olarak eger r displaystyle rho sabit farzedilirse su sistem elde edilir r vx t vx vx x vy vx y vz vx z m 2vx x2 2vx y2 2vx z2 p x rgx displaystyle rho left partial v x over partial t v x partial v x over partial x v y partial v x over partial y v z partial v x over partial z right mu left partial 2 v x over partial x 2 partial 2 v x over partial y 2 partial 2 v x over partial z 2 right partial p over partial x rho g x r vy t vx vy x vy vy y vz vy z m 2vy x2 2vy y2 2vy z2 p y rgy displaystyle rho left partial v y over partial t v x partial v y over partial x v y partial v y over partial y v z partial v y over partial z right mu left partial 2 v y over partial x 2 partial 2 v y over partial y 2 partial 2 v y over partial z 2 right partial p over partial y rho g y r vz t vx vz x vy vz y vz vz z m 2vz x2 2vz y2 2vz z2 p z rgz displaystyle rho left partial v z over partial t v x partial v z over partial x v y partial v z over partial y v z partial v z over partial z right mu left partial 2 v z over partial x 2 partial 2 v z over partial y 2 partial 2 v z over partial z 2 right partial p over partial z rho g z Sureklilik denklemi sikistirilamazlik kabulu ile vx x vy y vz z 0 displaystyle partial v x over partial x partial v y over partial y partial v z over partial z 0 Silindirik koordinatlar Navier Stokes Sureklilik denklemi silindirik koordinatlar icin soyledir ur r ur r 1 r u8 8 uz z displaystyle partial u r over partial r u r over r 1 over r partial u theta over partial theta partial u z over partial z 0 Silindirik koordinatlar icin Navier Stokes denklemleri de su sekilde yazilir r momentum r ur t ur ur r u8r ur 8 uz ur z u82r displaystyle rho left partial u r over partial t u r partial u r over partial r u theta over r partial u r over partial theta u z partial u r over partial z u theta 2 over r right P r m 2ux r2 1r ux r urr2 1r2 2ur 82 2ur z2 2r2 u8 8 Fr displaystyle partial P over partial r mu left partial 2 u x over partial r 2 1 over r partial u x over partial r u r over r 2 1 over r 2 partial 2 u r over partial theta 2 partial 2 u r over partial z 2 2 over r 2 partial u theta over partial theta right F r 8 displaystyle theta momentum r u8 t ur u8 r uru8r u8r u8 8 uz u8 z displaystyle rho left partial u theta over partial t u r partial u theta over partial r u r u theta over r u theta over r partial u theta over partial theta u z partial u theta over partial z right 1r P 8 m 2u8 r2 1r u8 r u8r2 1r2 2u8 82 2u8 z2 2r2 ur 8 F8 displaystyle 1 over r partial P over partial theta mu left partial 2 u theta over partial r 2 1 over r partial u theta over partial r u theta over r 2 1 over r 2 partial 2 u theta over partial theta 2 partial 2 u theta over partial z 2 2 over r 2 partial u r over partial theta right F theta z momentum r uz t ur uz r u8r uz 8 uz uz z displaystyle rho left partial u z over partial t u r partial u z over partial r u theta over r partial u z over partial theta u z partial u z over partial z right P z m 2uz r2 1r uz r 1r2 2uz 82 2uz z2 Fz displaystyle partial P over partial z mu left partial 2 u z over partial r 2 1 over r partial u z over partial r 1 over r 2 partial 2 u z over partial theta 2 partial 2 u z over partial z 2 right F z Sunu ifade etmek gerekir ki Navier Stokes denklemleri akiskan akisini sadece yaklasik olarak tanimlayabilir ve cok kucuk olceklerde veya sira disi sartlarda gercek akiskanlar diger maddeleri ve molekulleri iceren karisimlardir Navier Stokes denklemleri ile homojen ve surekli akislar modellenmis ve bunun uzerinden sonuclar elde edilmistir Bununla beraber Navier Stokes denklemleri pratikteki problemlerin cozumu icin genis bir aralikta faydali olur Ayrica bakinizAkiskan Akiskanlar dinamigi Mach Sayisi Sureklilik mekanigi Diferansiyel denklemlerKaynakcaIngilizce Wikipedia Navier Stokes denklemleri maddesi 13 Eylul 2006 tarihinde Wayback Machine sitesinde arsivlendi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State