Çok değişkenli kalkülüs veya Çok değişkenli hesaplama, matematik biliminin bir alt alanıdır. Bir değişkenli hesapların, birden fazla değişkenli fonksiyonlarla hesaplara yayılması ve tek değişken yerine çoklu değişken içeren fonksiyonların entegrasyonu olarak görülür. Matris, tensör, kısmi türev, çokkatlı integral, çizgi integrali, yüzey integrali, hacim integrali, Jacobi, Hesse, Gradyan gibi inceleme alanları vardır.
Tipik işlemler
Limit ve süreklilik
Çok değişkenli analizde limitler ve süreklilik çalışması, tek değişkenli fonksiyonlarla gösterilmeyen birçok sonuçları üretir.
Örneğin, kendi alanlarında farklı yollara yaklaşıldığında farklı sınırlar veren iki değişkenli skaler fonksiyonlar vardır. Örneğin, fonksiyon
noktaya orijinden geçen çizgiler boyunca yaklaştığında sıfıra 
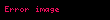
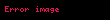

Her bir argümandaki sürekliliğin, çok değişkenli süreklilik için yeterli olmadığı da aşağıdaki örnekten görülebilir. Özellikle, gerçek değerli bir fonksiyonun, iki gerçek değerli parametre ile, 







Kısmi türev
Çoklu entegrasyon
Çok boyutlı hesaplamaların temel teoremleri
Uygulama alanları
Çok değişkenli analizin teknikleri, maddi dünyada ilgi duyulan birçok inceleyi gerçekleştirmek için kullanılır. Başta gelenleri şunlardır:
| Fonksiyon türleri | Uygulanabilir teknikler | ||
|---|---|---|---|
 | 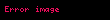  iken iken | Eğrilerin uzunlukları, çizgi integralleri ve eğrilik. | |
 | 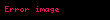 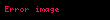 iken iken | Yüzeylerin alanları, yüzey integralleri, yüzeyler boyunca akış ve eğrilik. | |
| Sayıl alanlar |  | 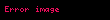 | Maksimum ve minimum, Lagrange çarpanları, yönlü türevler, . |
| Vektör alanı |  | 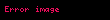 | Gradyan, diverjans veya rotasyonel içeren herhangi bir vektör hesabı işlemi. |
Kaynakça
Dış bağlantılar
| Wikimedia Commons'ta Çok değişkenli kalkülüs ile ilgili ortam dosyaları bulunmaktadır. |
- "Çok değişkenli Calculus MIT Video konferanslar" (İngilizce). 2 Temmuz 2014. 11 Haziran 2017 tarihinde kaynağından . Erişim tarihi: 3 Kasım 2019.
- "Çok değişkenli Matematik: George Cain ve James Herod tarafından ücretsiz çevrimiçi ders kitabı" (İngilizce). 1996. 14 Mayıs 2019 tarihinde kaynağından . Erişim tarihi: 3 Kasım 2019.
- "Çok Değişkenli Analiz: Jeff Knisley tarafından ücretsiz çevrimiçi ders kitabı" (İngilizce). Ocak 2014. 25 Mayıs 2019 tarihinde kaynağından . Erişim tarihi: 3 Kasım 2019.
- Perot, Prof. Blair (2011). "Çok Değişkenli Analiz - Çok Hızlı Bir İnceleme" (İngilizce). University of Massachusetts Amherst. 31 Mayıs 2019 tarihinde kaynağından . Erişim tarihi: 3 Kasım 2019.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Cok degiskenli kalkulus veya Cok degiskenli hesaplama matematik biliminin bir alt alanidir Bir degiskenli hesaplarin birden fazla degiskenli fonksiyonlarla hesaplara yayilmasi ve tek degisken yerine coklu degisken iceren fonksiyonlarin entegrasyonu olarak gorulur Matris tensor kismi turev cokkatli integral cizgi integrali yuzey integrali hacim integrali Jacobi Hesse Gradyan gibi inceleme alanlari vardir Tipik islemlerLimit ve sureklilik Cok degiskenli analizde limitler ve sureklilik calismasi tek degiskenli fonksiyonlarla gosterilmeyen bircok sonuclari uretir Ornegin kendi alanlarinda farkli yollara yaklasildiginda farkli sinirlar veren iki degiskenli skaler fonksiyonlar vardir Ornegin fonksiyon f x y x2yx4 y2 displaystyle f x y frac x 2 y x 4 y 2 noktaya orijinden gecen cizgiler boyunca yaklastiginda sifira 0 0 displaystyle 0 0 yaklasir y kx displaystyle y kx Ancak orijine bir parabol y x2 displaystyle y pm x 2 boyunca yaklastiginda fonksiyon degeri 0 5 displaystyle pm 0 5 ile sinirlanir Ayni noktaya dogru farkli yollar almak farkli limit degerleri verdiginden orada genel bir limit bulunmaz Her bir argumandaki surekliligin cok degiskenli sureklilik icin yeterli olmadigi da asagidaki ornekten gorulebilir Ozellikle gercek degerli bir fonksiyonun iki gercek degerli parametre ile f x y displaystyle f x y sabit y displaystyle y icin f displaystyle f nin x displaystyle x in devamliligi ve sabit x displaystyle x icin f displaystyle f nin y displaystyle y nin devamliligi f displaystyle f nin devamliligi anlamina gelmez Kismi turev Coklu entegrasyon Cok boyutli hesaplamalarin temel teoremleri Gradyan teoremi Stokes teoremi Green teoremiUygulama alanlariCok degiskenli analizin teknikleri maddi dunyada ilgi duyulan bircok inceleyi gerceklestirmek icin kullanilir Basta gelenleri sunlardir Fonksiyon turleri Uygulanabilir tekniklerf R Rn displaystyle f mathbb R to mathbb R n n gt 1 displaystyle n gt 1 iken Egrilerin uzunluklari cizgi integralleri ve egrilik f R2 Rn displaystyle f mathbb R 2 to mathbb R n n gt 2 displaystyle n gt 2 iken Yuzeylerin alanlari yuzey integralleri yuzeyler boyunca akis ve egrilik Sayil alanlar f Rn R displaystyle f mathbb R n to mathbb R Maksimum ve minimum Lagrange carpanlari yonlu turevler Vektor alani f Rm Rn displaystyle f mathbb R m to mathbb R n Gradyan diverjans veya rotasyonel iceren herhangi bir vektor hesabi islemi Kaynakca Cok Degiskenli Kalkulus 3 Kasim 2019 tarihinde kaynagindan Erisim tarihi 3 Kasim 2019 a b Richard Courant Fritz John 14 Aralik 1999 Introduction to Calculus and Analysis Ingilizce II 2 Springer Science amp Business Media ss 17 22 ISBN 978 3 540 66570 0 Dis baglantilarWikimedia Commons ta Cok degiskenli kalkulus ile ilgili ortam dosyalari bulunmaktadir Cok degiskenli Calculus MIT Video konferanslar Ingilizce 2 Temmuz 2014 11 Haziran 2017 tarihinde kaynagindan Erisim tarihi 3 Kasim 2019 Cok degiskenli Matematik George Cain ve James Herod tarafindan ucretsiz cevrimici ders kitabi Ingilizce 1996 14 Mayis 2019 tarihinde kaynagindan Erisim tarihi 3 Kasim 2019 Cok Degiskenli Analiz Jeff Knisley tarafindan ucretsiz cevrimici ders kitabi Ingilizce Ocak 2014 25 Mayis 2019 tarihinde kaynagindan Erisim tarihi 3 Kasim 2019 Perot Prof Blair 2011 Cok Degiskenli Analiz Cok Hizli Bir Inceleme Ingilizce University of Massachusetts Amherst 31 Mayis 2019 tarihinde kaynagindan Erisim tarihi 3 Kasim 2019
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State