Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
Fonksiyon, matematikte değişken sayıları girdi olarak kabul edip bunlardan bir çıktı sayısı oluşmasını sağlayan kurallardır. Fonksiyon, 17. yüzyılda matematiğin kavramlarından biri olmuştur. Fizik, mühendislik, mimarlık ve birçok alanda kullanılmaktadır. Galile, Kepler ve Newton hareketlerin araştırılmasında, zaman ve mesafe arasındaki durumu incelemek için fonksiyonlardan faydalanmıştır. Dört işlemden sonra gelen bir işlem türüdür.
Matematiksel tanım
Fonksiyonun matematiksel yani biçimsel ve kuramsal tanımı şu şekildedir:



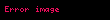
- Her
için,
ilişkisini sağlayan
- bir tane
elemanı vardır.
- Her
Bu durumda 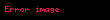

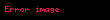







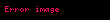


Fonksiyonu matematiksel olarak tanımlamak için bir kural zorunluluğu yoktur. Ama 
Eğer 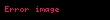
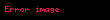

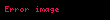
Örnekler




















Özet olarak, verilmiş bir 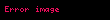


Yukarıdaki örnekte, kural, 




Yukarıda 
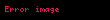


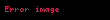



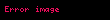


Bunun gibi, 
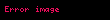

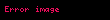



Aynı şekilde 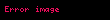
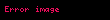
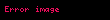


Yukarıda koyu renkle yazılı kelimeler şu nedenle önemlidir: Bir 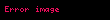









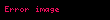

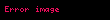




İkinci koyu renkli kısmın önemi ise şu şekildedir: Bir 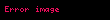




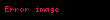


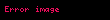



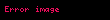




Tanım kümesi ve değer kümesi
Bir 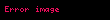


Görüntü

Eğer 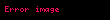




altkümesi 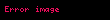

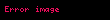

Mesela 


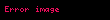
Fonksiyon eşitliği



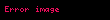
Durağan (sabit) fonksiyonlar









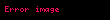




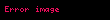

Bileşke mümkün olduğunda 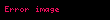

Eğer 



Boş fonksiyon
Eğer 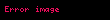
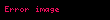

Eğer 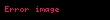



Özdeşlik fonksiyonu
Eğer 
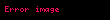

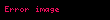

Bir fonksiyonun kısıtlanışı
Eğer 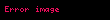
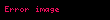


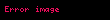

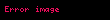
olarak yazılır ve bu fonksiyona 
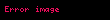

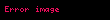
Varış kümesini değiştirmek
Bir fonksiyonun varış kümesini de değiştirilebilir: 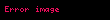
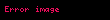

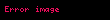


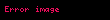
Fonksiyonların yapıştırılması ya da birleşimi

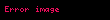







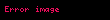
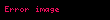
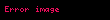
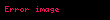
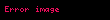


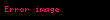

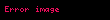
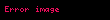


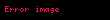


eğer
ise
eğer
ise.
Bu fonksiyona 


Mesela 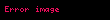

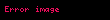

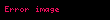
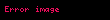
Elbette 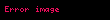
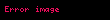
Gene doğal olarak 
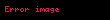
Yukarıdaki yapıştırmayı yapabilmemiz için 


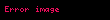
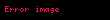





İkiden çok, hatta sonsuz tane fonksiyonu da yapıştırabiliriz eğer gerekli şartlar sağlanıyorsa: 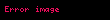


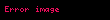
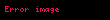

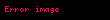
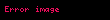

- "eğer
ise
"
- "eğer
kuralıyla tanımlanabilir. Bu tür yapıştırmalar topolojide ve analizde sık sık kullanılır.
Bir fonksiyonun altkümeler kümesinde neden olduğu fonksiyon. 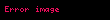




.
Bu 




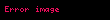


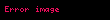
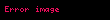
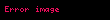


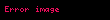





tanımı yerine,
tanımını yapmak daha yerinde olur.
Eğer 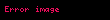


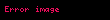


Alakalı maddeler




Gönderme örnekleri
- Doğal sayılarda bir sayının bir göndermedir.
- İki değişkenli göndermeler de vardır.
- Verilen sıraya karşılık gelen çift sayıyı söyleyen bağıntı bir göndermedir: f(n)=2n.
- Bir küme üzerinde tanımlı bir ikili işlem, göndermedir: f(x,y)=x+y.
- Diziler birer göndermedir.
- ise B kümesinde, eşlenmemiş en az bir değer vardır.
- Örten ise A kümesindeki bütün ögeler için tanımlıdır.
Matematiksel olarak; her y € B için en az bir x€A vardır öyle ki; f(x)=y'dir.
Bilgisayar bilimi ve göndermeler
Bilgisayarda göndermelere Türkçede genellikle adı verilir.
- Bilgisayar biliminde hesaplanabilir fonksiyonlar, birbirine eşdeğer olan Church ve Turing Tezleri ile incelenir.
- Girdisi ve çıktısı mantıksal ( ya da Boolean) olan fonksiyonlar, 'ler yardımıyla gösterilebilir.
Kaynakça
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu maddenin veya maddenin bir bolumunun gelisebilmesi icin matematik konusunda uzman kisilere gereksinim duyulmaktadir Ayrintilar icin lutfen tartisma sayfasini inceleyin veya yeni bir tartisma baslatin Konu hakkinda uzman birini bulmaya yardimci olarak ya da maddeye gerekli bilgileri ekleyerek Vikipedi ye katkida bulunabilirsiniz Subat 2009 Bu madde okuyucular icin kafa karistirici iceriklere veya net olmayan ifadelere sahip olabilir Lutfen ifadeleri netlestirmeye yardimci olun Maddenin tartisma sayfasinda konuyu tartisin Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Bu madde cogu okuyucunun anlayamayacagi kadar teknik olabilir Lutfen teknik detaylari cikarmadan maddeyi uzman olmayan okuyucular tarafindan anlasilabilir hale getirilmesine yardimci olun Kasim 2023 Bu madde olmasi gerekenden az ic baglanti icermektedir veya hic icermemektedir Lutfen bu sayfadan ilgili maddelere ic baglanti vermeye calisin Kasim 2021 Bu madde ansiklopedik bir icerik icin cok fazla veya cok uzun alintilar iceriyor Alintilari ozetleyerek maddenin iyilestirilmesine yardimci olun Dogrudan alintilari Vikisoz e aktarmayi dusunebilirsiniz Kasim 2021 Fonksiyon matematikte degisken sayilari girdi olarak kabul edip bunlardan bir cikti sayisi olusmasini saglayan kurallardir Fonksiyon 17 yuzyilda matematigin kavramlarindan biri olmustur Fizik muhendislik mimarlik ve bircok alanda kullanilmaktadir Galile Kepler ve Newton hareketlerin arastirilmasinda zaman ve mesafe arasindaki durumu incelemek icin fonksiyonlardan faydalanmistir Dort islemden sonra gelen bir islem turudur Matematiksel tanimFonksiyonun matematiksel yani bicimsel ve kuramsal tanimi su sekildedir A displaystyle A ve B displaystyle B iki kume olmak uzere ve F displaystyle F A B displaystyle A times B kartezyen carpiminin su ozelligini saglayan bir alt kumesi olmak uzere Her x A displaystyle x in A icin x y F displaystyle x y in F iliskisini saglayan bir tane y B displaystyle y in B elemani vardir dd Bu durumda A B F displaystyle A B F uclusune fonksiyon adi verilir A displaystyle A A B F displaystyle A B F fonksiyonunun tanim kumesidir B displaystyle B ise varis goruntu kumesidir A B F displaystyle A B F fonksiyonuna f displaystyle f adi verilirse verilen bir x A displaystyle x in A icin B displaystyle B nin x y F displaystyle x y in F iliskisini saglayan tek y displaystyle y elemani f x displaystyle f x olarak gosterilir Kimi zaman f x displaystyle f x yerine fx displaystyle fx yazildigi da olur Yani her x X displaystyle x in X icin x fx F displaystyle x fx in F olur Ayrica F displaystyle F kumesine f displaystyle f fonksiyonunun grafigi adi verilir Fonksiyonu matematiksel olarak tanimlamak icin bir kural zorunlulugu yoktur Ama F displaystyle F nin bir kume olma zorunlulugu vardir Eger A displaystyle A emptyset ise A B F displaystyle A B F uclusunun bir fonksiyon olabilmesi icin F displaystyle F nin bos kume olmasi gerektigi aciktir bu durumda bu B displaystyle emptyset B emptyset uclusu bos fonksiyondur Cizgileri dusey dogrulari hepsi grafigi yalniz bir noktada kestigi icin f x fonksiyondur OrneklerA displaystyle A ve B displaystyle B iki kume ise A displaystyle A nin her elemanini bir sekilde B displaystyle B nin bir ve bir tek elemaniyla iliskilendirilmistir Mesela A R displaystyle A mathbb R gercel sayilar kumesi B displaystyle B de 3 ten buyuk gercel sayilar kumesi olsun yani B 3 displaystyle B 3 infty olsun Iliskilendirme de soyle yapilmali A displaystyle A nin her elemanini yani her gercel sayiyi o elemanin karesiyle iliskilendirilmis olsun Boylece iliskilendirmeyi bir formulle tanimlamis olduk Bu ornekteki iliskilendirmeyi x x2 displaystyle x mapsto x 2 olarak yazariz her sayi karesiyle iliskilendirilmistir mesela 3 sayisi 9 la 2 displaystyle sqrt 2 sayisi 2 yle iliskilendirilmistir Iste A displaystyle A dan B displaystyle B ye giden fonksiyon boyle bir seydir Fonksiyon f displaystyle f semboluyle ifade edilir Verilen ornek icin f x x2 displaystyle f x x 2 yazilir A displaystyle A yasamis ya da su anda yasayan insanlar kumesi olsun f displaystyle f fonksiyonu her insani annesine gotursun Matematiksel olmasa da bu A displaystyle A dan A displaystyle A ya giden bir fonksiyondur cunku her insanin bir annesi vardir Ama her insani kardesine goturen bir fonksiyon yoktur cunku bazi insanlarin kardesi olmadigi gibi bazi insanlarin birden cok kardesi vardir Ote yandan her insani en buyuk kardesine goturen kural kardesi olan insanlar kumesinden A displaystyle A kumesine giden bir fonksiyondur A displaystyle A dan B displaystyle B ye giden bir f A B displaystyle f A longrightarrow B fonksiyonu A displaystyle A kumesinin her elemanini B displaystyle B nin bir ve bir tek elemanina goturen elemaniyla iliskilendiren bir kural dir Burada biraz yalan var ama pek onemli degil Kuralin ne demek oldugunu soylemedigimiz gibi bir fonksiyonun tanimlanmasi icin herhangi bir kurala da aslinda gerek yoktur Ileride yazinin sonunda fonksiyonun gercek matematiksel tanimini verdigimizde bu pembe yalana ihtiyacimiz kalmayacak Ozet olarak verilmis bir f A B displaystyle f A longrightarrow B fonksiyonu A displaystyle A nin her elemanini bir sekilde B displaystyle B nin bir ve bir tek elemanina goturur elemaniyla iliskilendirir Yukaridaki ornekte kural f x x2 displaystyle f x x 2 olarak verilmistir Ama bir fonksiyon bir formul ya da bir kuraldan ote bir seydir Bir fonksiyon sadece bir kural degildir bir fonksiyonu tanimlamak icin kural disinda bir de ayrica A displaystyle A ve B displaystyle B kumeleri de gerekmektedir Formul ya da kural ayni kalsa bile A displaystyle A ve B displaystyle B kumeleri degisirse fonksiyon da degisir Yukaridaki ornek uzerinden gidelim Yukarida A displaystyle A R ve B 3 displaystyle B 3 infty almis ve fonksiyonu f x x2 displaystyle f x x 2 kuraliyla tanimlanmisti Simdi A displaystyle A yerine A1 5 displaystyle A 1 5 infty alirsak ve formulu ve B displaystyle B kumesini ayni tutarsak o zaman elde edilen A1 B displaystyle A 1 longrightarrow B fonksiyonunu gene f displaystyle f ile gostermek yanlis olur cunku bu iki fonksiyon degisik fonksiyonlardir A1 displaystyle A 1 den B displaystyle B ye giden ve kare alma kuraliyla tanimlanan fonksiyonu mesela g displaystyle g ile gosterilebilir Bunun gibi B displaystyle B kumesi degisirse o zaman fonksiyon da degisir mesela B1 0 displaystyle B 1 0 infty ise kare alma kurali A displaystyle A dan B1 displaystyle B 1 e giden bir fonksiyon tanimlar ve bu fonksiyon yukaridakilerle karismasin diye f displaystyle f ya da g displaystyle g ile degil bir baska sembolle mesela h displaystyle h ile gosterilir Ayni sekilde A1 displaystyle A 1 den B1 displaystyle B 1 e giden bir fonksiyon f g displaystyle f g ya da h displaystyle h ile degil mesela k displaystyle k ile gosterilmelidir Yukarida koyu renkle yazili kelimeler su nedenle onemlidir Bir f A B displaystyle f A longrightarrow B fonksiyonu A displaystyle A kumesinin her elemanini B displaystyle B nin bir elemanina goturur yani A displaystyle A nin bazi elemanlarini unutmus olamaz Mesela karekok alma kurali gercel sayilar kumesi R displaystyle mathbb R den R displaystyle mathbb R ye giden bir fonksiyon tanimlamaz cunku negatif sayilarin gercel sayilarda karekoku yoktur Ya da A B N displaystyle A B mathbb N dogal sayilar kumesi ise f x x 1 displaystyle f x x 1 kurali A displaystyle A dan B displaystyle B ye giden bir fonksiyon tanimlamaz cunku f 0 1 displaystyle f 0 1 dir ve 0 A displaystyle 0 in A olmasina karsin 1 displaystyle 1 sayisi B displaystyle B de degildir Ote yandan bu f x x 1 displaystyle f x x 1 kurali N displaystyle mathbb N den tam sayilar kumesi Z displaystyle mathbb Z ye giden bir fonksiyon tanimlar Ikinci koyu renkli kismin onemi ise su sekildedir Bir f A B displaystyle f A longrightarrow B fonksiyonu A displaystyle A nin her elemanini B displaystyle B nin bir ve bir tek elemanina goturur yani A displaystyle A nin ayni elemani B displaystyle B nin iki ayri elemanina gidemez Yukarida verilen kardes misali hatirlanmali Mesela A B R displaystyle A B mathbb R ise A displaystyle A nin bir x displaystyle x elemanini x2 y2 displaystyle x 2 y 2 denkleminin y displaystyle y cozumlerine goturemez cunku eger x 0 displaystyle x 0 degilse bu denklemin R de iki degisik y displaystyle y cozumu vardir nitekim x2 y2 displaystyle x 2 y 2 denkleminin cozumleri y x displaystyle y x ve y x displaystyle y x tir Burada y displaystyle y nin x displaystyle x e mi yoksa x displaystyle x e mi gidecegi belirtilmemistir ve bu bir fonksiyon yaratmada sorun teskil eder Bir f A B displaystyle f A longrightarrow B fonksiyonunda A displaystyle A nin her elemanini B displaystyle B nin bir ve bir tek elemanina gitmelidir iki ya da daha fazla elemana gidemez Birkac yuzyil once bu tur fonksiyonlar kabul ediliyordu ama bugun bunlara fonksiyon denmiyor Tanim kumesi ve deger kumesiBir f A B displaystyle f A longrightarrow B fonksiyonunda A displaystyle A ya tanim kumesi ya da kalkis kumesi denir B displaystyle B ye de deger kumesi ya da varis kumesi denir GoruntuKarmasik ustel grafigin yuzey grafikleri fonksiyonu Eger x A displaystyle x in A ise f x displaystyle f x e x displaystyle x in f displaystyle f altinda goruntusu adi verilir B displaystyle B nin f x x A displaystyle f x x in A dd altkumesi f A displaystyle f A olarak gosterilir ve bu kumeye f displaystyle f nin goruntu kumesi adi verilir Kimi f A displaystyle f A yerine B displaystyle B ye goruntu kumesi demeyi yegliyor ama her zaman goruntu kumesi deger kumesine esit olmak zorunda degildir Mesela f x x2 displaystyle f x x 2 kuraliyla tanimlanan f displaystyle f 3 5 displaystyle longrightarrow R fonksiyonunun goruntu kumesi 0 25 displaystyle 0 25 araligidir Fonksiyon esitligif displaystyle f ve g displaystyle g fonksiyonlarinin birbirine esit olmasi icin 1 tanim kumelerinin esit olmasi 2 deger kumelerinin esit olmasi ve 3 tanim kumesindeki her x displaystyle x icin f x g x displaystyle f x g x olmasi gerekmektedir Bu uc sarttan biri eksikse fonksiyonlar esit olmaz Genellikle liselerde sadece ucuncu sart uzerinde durulur Gene de esitlikte en onemli sart 3 sartidir Ardindan 1 sarti gelir 2 sartinin gozden kactigi olur Duragan sabit fonksiyonlarA displaystyle A ve B displaystyle B iki kume olsun ve b B displaystyle b in B olsun A displaystyle A nin her elemanini B displaystyle B nin bu b displaystyle b elemanina goturen fonksiyona sabit fonksiyon adi verilir b displaystyle b degerini alan sabit fonksiyonu cb displaystyle c b olarak gosterirsek o zaman cb lt zvxcvcxvcxvcxvcvxcbcv A B displaystyle c b lt zvxcvcxvcxvcxvcvxcbcv A longrightarrow B fonksiyonu her x A displaystyle x in A icin cb x b displaystyle c b x b kuraliyla tanimlanir Not A displaystyle A ve B displaystyle B kumelerinin onemini ortaya cikarmak istiyorsak cb displaystyle c b yerine cb A B displaystyle c b A B yazmak gerekebilir Bu fonksiyona sabit b displaystyle b fonksiyonu adi verilir Bileske mumkun oldugunda cb f cb displaystyle c b circ f c b dir Ama f cb cf c displaystyle f circ c b c f c dir Eger A displaystyle A ya da B displaystyle B nin tek bir elemani varsa o zaman A displaystyle A dan B displaystyle B ye giden her fonksiyon sabit olmak zorundadir Bos fonksiyonEger A displaystyle A neq emptyset ve B displaystyle B emptyset ise A displaystyle A longrightarrow B displaystyle B ye giden bir fonksiyon yoktur Eger A displaystyle A emptyset ise B displaystyle B hangi kume olursa olsun A displaystyle A dan B displaystyle B ye giden bir ve tek fonksiyon vardir bos fonksiyon Pek de onemli olmayan bu olgu birazdan fonksiyonun matematiksel tanimi verdigimizde bariz olacak Ozdeslik fonksiyonuEger A displaystyle A bir kumeyse her x A displaystyle x in A icin IdA x x displaystyle A x x kuraliyla tanimlanan IdA A A displaystyle A A longrightarrow A fonksiyonuna A displaystyle A nin ozdeslik fonksiyonu adi verilir Ozdeslik fonksiyonu bileskenin sagdan ve soldan Bir fonksiyonun kisitlanisiEger f A B displaystyle f A longrightarrow B bir fonksiyonsa ve A1 A displaystyle A 1 subseteq A A displaystyle A nin bir altkumesiyse o zaman f displaystyle f fonksiyonunu A1 displaystyle A 1 altkumesine kisitlayabiliriz yani f displaystyle f nin sadece A1 displaystyle A 1 kumesinin elemanlarinda alacagi degerlerle ilgilenilebilir Bu yeni fonksiyon f A1 A1 B displaystyle f A 1 A 1 longrightarrow B dd olarak yazilir ve bu fonksiyona f displaystyle f nin A1 displaystyle A 1 e adi verilir Elbette eger A2 A1 A displaystyle A 2 subseteq A 1 subseteq A ise f A1 A2 f A2 displaystyle f A 1 A 2 f A 2 esitligi gecerlidir Varis kumesini degistirmekBir fonksiyonun varis kumesini de degistirilebilir f A B displaystyle f A longrightarrow B bir fonksiyon olsun B1 displaystyle B 1 f displaystyle f nin goruntu kumesi f A displaystyle f A yi altkume olarak iceren herhangi bir kume olsun O zaman A displaystyle A tanim kumesini ve f displaystyle f kuralini degistirmeden yeni bir g A B1 displaystyle g A longrightarrow B 1 fonksiyonu elde edilebilir Bu fonksiyon daha onceki paragraftaki gibi ozel bir sembolle gosterilmez Fonksiyonlarin yapistirilmasi ya da birlesimif A V displaystyle f A longrightarrow V ve g B V displaystyle g B longrightarrow V iki fonksiyon olsun A displaystyle A uzerinde f displaystyle f olan B displaystyle B uzerinde g displaystyle g olan ve A B displaystyle A cup B den V displaystyle V ye giden bir f g displaystyle f cup g fonksiyonu tanimlamak istiyoruz Eger x A B displaystyle x in A setminus B ise f g x f x displaystyle f cup g x f x olmali Eger x B A displaystyle x in B setminus A ise f g x g x displaystyle f cup g x g x olmali Ama x A B displaystyle x in A cap B oldugunda f g x displaystyle f cup g x icin f x displaystyle f x ya da g x displaystyle g x arasinda bir secim yapmaliyiz ozellikle eger f x g x displaystyle f x neq g x ise Bu durumda hangi secimi yapilirsa yapilsin istedigimiz iki sarttan birini cignemek zorunda kalacagiz Ama diyelim ki her x A B displaystyle x in A cap B icin f x g x displaystyle f x g x yani f displaystyle f ve g displaystyle g fonksiyonlari A B displaystyle A cap B kesisiminde aldiklari deger ayni bir baska deyisle f A B g A B displaystyle f A cap B g A cap B O zaman f g A B V displaystyle f cup g A cup B longrightarrow V fonksiyonunu herhangi bir secime gerek kalmadan soyle tanimlayabiliriz f g x f x displaystyle f cup g x f x eger x A displaystyle x in A ise dd f g x g x displaystyle f cup g x g x eger x B displaystyle x in B ise dd Bu fonksiyona f displaystyle f ve g displaystyle g fonksiyonlarinin birlesimi ya da yapistirilmasi adi verilir ve yukarida gosterildigi gibi bu fonksiyon f g displaystyle f cup g olarak yazilir Mesela f 0 R displaystyle f 0 infty longrightarrow mathbb R fonksiyonu f x x displaystyle f x x olarak tanimlanmissa ve g 0 R displaystyle g infty 0 longrightarrow mathbb R fonksiyonu g x x displaystyle g x x olarak tanimlanmissa o zaman f g A B R displaystyle f cup g A cup B longrightarrow mathbb R fonksiyonu aynen mutlak deger fonksiyonudur f g x x displaystyle f cup g x x Elbette f g A f displaystyle f cup g A f ve f g B g displaystyle f cup g B g Gene dogal olarak f g displaystyle f cup g diye bir fonksiyon varsa g f displaystyle g cup f diye bir fonksiyon de vardir ve bu iki fonksiyon birbirine esittir Yukaridaki yapistirmayi yapabilmemiz icin f displaystyle f ve g displaystyle g fonksiyonlarinin varis kumeleri ayni olmak zorunda degildi Nitekim eger f A U displaystyle f A longrightarrow U ve g B V displaystyle g B longrightarrow V iki fonksiyon ise ve bu fonksiyonlarin A B displaystyle A cap B kumesinde aldiklari deger esitse o zaman A displaystyle A uzerinde f displaystyle f olan B displaystyle B uzerinde g displaystyle g olan bir f g A B U V displaystyle f cup g A cup B longrightarrow U cup V fonksiyonunu gene tanimlayabiliriz Ikiden cok hatta sonsuz tane fonksiyonu da yapistirabiliriz eger gerekli sartlar saglaniyorsa fi Ai Vi i I displaystyle f i A i longrightarrow V i i in I bir olsun Ayrica her i j I displaystyle i j in I endisleri icin fi displaystyle f i ve fj displaystyle f j fonksiyonlarinin Ai Aj displaystyle A i cap A j kesisiminde aldiklari degerler esit olsun O zaman her i I displaystyle i in I ve her x Ai displaystyle x in A i icin i Ifi x fi x displaystyle cup i in I f i x f i x esitligini saglayan bir i Ifi i IVi displaystyle cup i in I f i longrightarrow cup i in I V i fonksiyonu eger x Xi displaystyle x in X i ise i Ifi x fi x displaystyle cup i in I f i x f i x dd kuraliyla tanimlanabilir Bu tur yapistirmalar topolojide ve analizde sik sik kullanilir Bir fonksiyonun altkumeler kumesinde neden oldugu fonksiyon f A B displaystyle f A longrightarrow B bir fonksiyon olsun A displaystyle A nin her X displaystyle X altkumesi icin B displaystyle B nin f X displaystyle f X altkumesi soyle tanimlanir f X f x x X displaystyle f X f x x in X dd Bu f X displaystyle f X yazilimi ender de olsa soruna yol acabilir cunku A displaystyle A nin X displaystyle X altkumesi bal gibi de ayni zamanda A displaystyle A nin bir elemani olabilir o zaman f X displaystyle f X ifadesinin f A B displaystyle f A longrightarrow B fonksiyonunun X displaystyle X te aldigi deger mi oldugu yoksa yukaridaki gibi B displaystyle B nin altkumesi olarak mi tanimlandigi anlasilamaz Mesela A 0 0 displaystyle A 0 0 olsun B 5 6 displaystyle B 5 6 olsun f A B displaystyle f A longrightarrow B fonksiyonu f 0 5 displaystyle f 0 5 f 0 6 displaystyle f 0 6 olarak tanimlansin Ve son olarak X 0 displaystyle X 0 olsun X displaystyle X hem A displaystyle A nin bir elemani hem de bir alt kumesidir X displaystyle X eleman olarak goruldugunde f X 6 displaystyle f X 6 olur ama altkume olarak goruldugunde f X 5 displaystyle f X 5 olur Belki bu yuzden f X f x x X displaystyle f X f x x in X dd tanimi yerine f X f x x X displaystyle tilde f X f x x in X dd tanimini yapmak daha yerinde olur Eger P X displaystyle P X X displaystyle X in alt kumeleri kumesiyse yukaridaki f displaystyle tilde f kurali P X displaystyle P X ten P Y displaystyle P Y ye giden bir fonksiyon tanimlar Bu f displaystyle tilde f fonksiyonu altkume olma iliskisine saygi duyar Alakali maddelerBileske fonksiyon Birebir fonksiyon Esleme Eslesme Orten fonksiyonX kumesindeki her eleman bir giris Y kumesindeki bir elemanla mutlaka eslenmelidir bir cikis Bu gosterim bir fonksiyon fonksiyon degildir Bir girise iki cikis vardir Ornek bir fonksiyon fonksiyon grafigi f 1 1 5 1 1 5 x 4x3 6x2 1 x 13 x displaystyle begin aligned amp scriptstyle f colon 1 1 5 to 1 1 5 amp textstyle x mapsto frac 4x 3 6x 2 1 sqrt x 1 3 x end aligned Gonderme ornekleriDogal sayilarda bir sayinin bir gondermedir g N N A x x 1 displaystyle g mathbb N rightarrow mathbb N A x x 1 dd Iki degiskenli gondermeler de vardir h R R R h x y x2 y2 displaystyle h mathbb R times mathbb R rightarrow mathbb R h x y x 2 y 2 dd Verilen siraya karsilik gelen cift sayiyi soyleyen baginti bir gondermedir f n 2n Bir kume uzerinde tanimli bir ikili islem gondermedir f x y x y Diziler birer gondermedir ise B kumesinde eslenmemis en az bir deger vardir Orten ise A kumesindeki butun ogeler icin tanimlidir Matematiksel olarak her y B icin en az bir x A vardir oyle ki f x y dir Bilgisayar bilimi ve gondermelerBilgisayarda gondermelere Turkcede genellikle adi verilir Bilgisayar biliminde hesaplanabilir fonksiyonlar birbirine esdeger olan Church ve Turing Tezleri ile incelenir Girdisi ve ciktisi mantiksal ya da Boolean olan fonksiyonlar ler yardimiyla gosterilebilir Kaynakca prezi com 17 Subat 2021 tarihinde kaynagindan arsivlendi Erisim tarihi 22 Subat 2023 Adams Robert A 2018 Calculus a complete course Pearson s 23 ISBN 9780134154367 3 Aralik 2021 tarihinde kaynagindan arsivlendi Ayrica bakinizMatematiksel fonksiyonlarin listesi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State