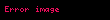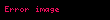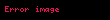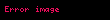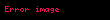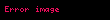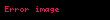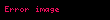Bileşke fonksiyon, matematikte bir işlevdir.
, kümesinden kümesine giden bir fonksiyonsa, de kümesinden kümesine giden bir fonksiyonsa, o zaman fonksiyonunu her için,
kuralıyla tanımlanan kümesinden kümesine giden fonksiyon olarak tanımlanır. Bu fonksiyona ve fonksiyonlarının bileşkesi adı verilir.
Başka bir deyişle, bileşke
- ve
fonksiyonlarından
fonksiyonunu üretir.
ve fonksiyonlarının (bu sırayla) bileşkesini alabilmek için fonksiyonunun değer kümesi, fonksiyonunun tanım kümesine eşit olmalıdır.
Eğer , kümesinden kümesine, de kümesinden kümesine giden bir fonksiyonsa, o zaman hem fonksiyonundan hem de fonksiyonundan söz edilebilir.
Bileşke, 'ten 'e giden fonksiyonlar kümesi olan Fonk kümesi üzerine bir ikili işlemdir. Özdeşlik fonksiyonu Id, bu ikili işlemin sağdan ve soldan etkisiz elemanıdır. Ayrıca, Fonk kümesinin bileşke işlemi için tersinir elemanları eşlemeler, yani bijeksiyonlardır.
Özellikleri
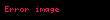




dir. Ancak
dir. Demek ki
,
yani bileşkenin değişme özelliği yoktur. Öte yandan bileşkenin birleşme özelliği vardır.
dört küme olsun.
,
,
üç fonksiyon olsun. O zaman şu fonksiyonlardan söz edilebilir:
,
,
,
.
Bu fonksiyonlardan ikincisi ve dördüncüsü birbirine eşittir, yani
eşitliği geçerlidir. 


ve
eşitliklerine ulaşılır.
Her iki eşitliğin sağ tarafları eşit olduğundan sol tarafları da eşittir, yani
.
Bundan da fonksiyonların eşit olduğu, yani 
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bileske fonksiyon matematikte bir islevdir f displaystyle f X displaystyle X kumesinden Y displaystyle Y kumesine giden bir fonksiyonsa g displaystyle g de Y displaystyle Y kumesinden Z displaystyle Z kumesine giden bir fonksiyonsa o zaman g f displaystyle g circ f fonksiyonunu her x X displaystyle x in X icin g f x g f x displaystyle g circ f x g f x dd kuraliyla tanimlanan X displaystyle X kumesinden Z displaystyle Z kumesine giden fonksiyon olarak tanimlanir Bu fonksiyona g displaystyle g ve f displaystyle f fonksiyonlarinin bileskesi adi verilir Baska bir deyisle bileske f X Y displaystyle f X longrightarrow Y ve g Y Z displaystyle g Y longrightarrow Z dd fonksiyonlarindan g f X Z displaystyle g circ f X longrightarrow Z dd fonksiyonunu uretir g displaystyle g ve f displaystyle f fonksiyonlarinin bu sirayla bileskesini alabilmek icin f displaystyle f fonksiyonunun deger kumesi g displaystyle g fonksiyonunun tanim kumesine esit olmalidir Eger f displaystyle f X displaystyle X kumesinden Y displaystyle Y kumesine g displaystyle g de Y displaystyle Y kumesinden X displaystyle X kumesine giden bir fonksiyonsa o zaman hem g f X X displaystyle g circ f X longrightarrow X fonksiyonundan hem de f g Y Y displaystyle f circ g Y longrightarrow Y fonksiyonundan soz edilebilir Bileske X displaystyle X ten X displaystyle X e giden fonksiyonlar kumesi olan Fonk X X displaystyle X X kumesi uzerine bir ikili islemdir Ozdeslik fonksiyonu IdX displaystyle X bu ikili islemin sagdan ve soldan etkisiz elemanidir Ayrica Fonk X X displaystyle X X kumesinin bileske islemi icin tersinir elemanlari eslemeler yani bijeksiyonlardir OzellikleriX Y Z R displaystyle X Y Z R gercek sayilar kumesi olsun f displaystyle f fonksiyonu f x x2 displaystyle f x x 2 ve g displaystyle g fonksiyonu g x x 1 displaystyle g x x 1 olarak tanimlansin O zaman f g x f g x f x 1 x 1 2 displaystyle f circ g x f g x f x 1 x 1 2 dd dir Ancak g f x g f x g x2 x2 1 displaystyle g circ f x g f x g x 2 x 2 1 dd dir Demek ki f g g f displaystyle f circ g neq g circ f dd yani bileskenin degisme ozelligi yoktur Ote yandan bileskenin birlesme ozelligi vardir X Y Z T displaystyle X Y Z T dort kume olsun dd f X Y displaystyle f X longrightarrow Y dd g Y Z displaystyle g Y longrightarrow Z dd h Z T displaystyle h Z longrightarrow T dd uc fonksiyon olsun O zaman su fonksiyonlardan soz edilebilir g f X Z displaystyle g circ f X longrightarrow Z dd h g f X T displaystyle h circ g circ f X longrightarrow T dd h g Y T displaystyle h circ g Y longrightarrow T dd h g f X T displaystyle h circ g circ f X longrightarrow T dd Bu fonksiyonlardan ikincisi ve dorduncusu birbirine esittir yani h g f h g f displaystyle h circ g circ f h circ g circ f dd esitligi gecerlidir X displaystyle X kumesinden herhangi bir x displaystyle x elemani alinir ve her iki fonksiyon da bu x displaystyle x elemaninda degerlendirilirse h g f x h g f x h g f x displaystyle h circ g circ f x h circ g f x h g f x dd ve h g f x h g f x h g f x displaystyle h circ g circ f x h g circ f x h g f x dd esitliklerine ulasilir Her iki esitligin sag taraflari esit oldugundan sol taraflari da esittir yani h g f x h g f x displaystyle h circ g circ f x h circ g circ f x dd Bundan da fonksiyonlarin esit oldugu yani h g f h g f displaystyle h circ g circ f h circ g circ f esitligi cikar
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State