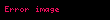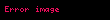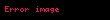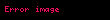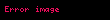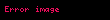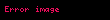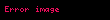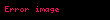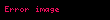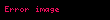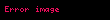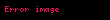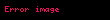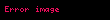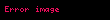Eğer bir kümeyse, kümesinden kümesine giden bir fonksiyona kümesi üzerine ikili işlem denir. İkili işlemi olarak gösterirsek, yerine genellikle , , ya da daha yaygın olarak yazmak bir gelenek halini almıştır. Burada önemli olan, her için, işlemin sonucu olan elemanının yine kümesinde olmasıdır, yoksa ikili bir işlemden söz edemeyiz. Örneğin, (doğal sayılar kümesi) ise, işlemi bu küme üzerinde ikili bir işlem değildir. Örneğin, bir doğal sayı değildir. Öte yandan olarak tanımlanan işlem doğal sayılar kümesi üzerine ikili bir işlemdir.
İkili işlem yerine kısaca "işlem" denildiği de olur.
yazılımı sadece işlem değişmeli olduğunda, yani kümedeki her için olduğunda kullanılır.
İşlemlerde genellikle her elemanı için eşitliği aranır, örneğin elemanından rahatça (yani özel bir tanıma gerek kalmadan) söz edebilmek için eşitliği geçerli olmalıdır. Bu özelliğe birleşme özelliği adı verilir.
Eğer her için ex = x eşitliğini sağlayan bir elemanı varsa, e'ye işlemin adı verilir. benzer biçimde tanımlanır. Soldan ve sağdan etkisiz elemanlar eşit olmak zorundadırlar, nitekim eğer e soldan, f de sağdan etkisizse olur. Öte yandan bir işlemde sağdan etkisiz eleman yoksa birden fazla soldan etkisiz eleman olabilir. Örneğin olarak tanımlanan işlemde her soldan etkisizdir; ve eğer kümede birden fazla eleman varsa bu işlemin sağdan etkisiz elemanı yoktur. Sağdan ve soldan etkisiz olan elemana kısaca etkisiz eleman denir.
Eğer her için ax = a ise a'ya soldan yutan eleman denir. Sağdan yutan eleman benzer biçimde tanımlanır. Soldan ve sağdan yutan elemanlar - olduklarında - eşittirler, çünkü eğer a soldan, b de sağdan yutansa, o zaman olur.
Matematiğin en önemli işlemlerinden biri fonksiyonların bileşke işlemidir. Eğer X bir kümeyse, Fonk(X, X), X kümesinden X kümesine giden fonksiyonlar kümesi olsun. Eğer Fonk(X, X) ise, gene X kümesinden X kümesine giden ve adına "f ile g fonksiyonlarının bileşkesi" denilen f o g fonksiyonunu şöyle tanımlayalım: Her için, (f o g)(x) = f(g(x)) olsun. Bu, Fonk(X, X) kümesi üzerine bir işlemdir. Bu işlemin birleşme özelliği vardır ama değişmeli değildir ve ayrıca etkisiz elemanı Id olarak gösterilen özdeşlik fonksiyonudur.
Ayrıca bakınız
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Eger X displaystyle X bir kumeyse X X displaystyle X times X kumesinden X displaystyle X kumesine giden bir fonksiyona X displaystyle X kumesi uzerine ikili islem denir Ikili islemi f X X X displaystyle f X times X longrightarrow X olarak gosterirsek f x y displaystyle f x y yerine genellikle x y displaystyle x y x y displaystyle x times y x y displaystyle x star y ya da daha yaygin olarak xy displaystyle xy yazmak bir gelenek halini almistir Burada onemli olan her x y X displaystyle x y in X icin islemin sonucu olan x y displaystyle x star y elemaninin yine X displaystyle X kumesinde olmasidir yoksa ikili bir islemden soz edemeyiz Ornegin X N displaystyle X N dogal sayilar kumesi ise x y displaystyle x y islemi bu kume uzerinde ikili bir islem degildir Ornegin 5 7 2 displaystyle 5 7 2 bir dogal sayi degildir Ote yandan x y 3 xy x y displaystyle x star y 3 xy x y olarak tanimlanan islem dogal sayilar kumesi uzerine ikili bir islemdir Ikili islem yerine kisaca islem denildigi de olur x y displaystyle x y yazilimi sadece islem degismeli oldugunda yani kumedeki her x y displaystyle x y icin x y y x displaystyle x star y y star x oldugunda kullanilir Islemlerde genellikle her x y z displaystyle x y z elemani icin x y z x y z displaystyle x star y star z x star y star z esitligi aranir ornegin x3 displaystyle x 3 elemanindan rahatca yani ozel bir tanima gerek kalmadan soz edebilmek icin x x x x x x displaystyle x star x star x x star x star x esitligi gecerli olmalidir Bu ozellige birlesme ozelligi adi verilir Eger her x X displaystyle x in X icin ex x esitligini saglayan bir e X displaystyle e in X elemani varsa e ye islemin adi verilir benzer bicimde tanimlanir Soldan ve sagdan etkisiz elemanlar esit olmak zorundadirlar nitekim eger e soldan f de sagdan etkisizse e ef f displaystyle e ef f olur Ote yandan bir islemde sagdan etkisiz eleman yoksa birden fazla soldan etkisiz eleman olabilir Ornegin x y y displaystyle x star y y olarak tanimlanan islemde her x X displaystyle x in X soldan etkisizdir ve eger kumede birden fazla eleman varsa bu islemin sagdan etkisiz elemani yoktur Sagdan ve soldan etkisiz olan elemana kisaca etkisiz eleman denir Eger her x X displaystyle x in X icin ax a ise a ya soldan yutan eleman denir Sagdan yutan eleman benzer bicimde tanimlanir Soldan ve sagdan yutan elemanlar olduklarinda esittirler cunku eger a soldan b de sagdan yutansa o zaman a ab b displaystyle a ab b olur Matematigin en onemli islemlerinden biri fonksiyonlarin bileske islemidir Eger X bir kumeyse Fonk X X X kumesinden X kumesine giden fonksiyonlar kumesi olsun Eger f g displaystyle f g in Fonk X X ise gene X kumesinden X kumesine giden ve adina f ile g fonksiyonlarinin bileskesi denilen f o g fonksiyonunu soyle tanimlayalim Her x X displaystyle x in X icin f o g x f g x olsun Bu Fonk X X kumesi uzerine bir islemdir Bu islemin birlesme ozelligi vardir ama degismeli degildir ve ayrica etkisiz elemani IdX displaystyle X olarak gosterilen ozdeslik fonksiyonudur Ayrica bakinizIslem Obek Grup matematik Halka Cisim Soyut cebirMatematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State