Hacim integrali çok değişkenli kalkülüsteki çokkatlı integralin 3 boyutlu durumudur. Hacim integrali fizikte önemli bir yere sahiptir. Özellikle yoğunlukların hesabı için kullanılır.
Kartezyen koordinat sisteminde
Hacim integrali 
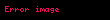
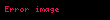
Bu integral silindirik koordinat sisteminde şöyle yazılır:
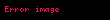
Küresel koordinat sisteminde ise şöyle bir yazım mevcuttur:
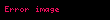
Örnek

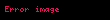
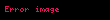

Fizikte

Burada 

Aynı şekilde farklı büyüklüklerin yoğunluğu alınabilir.Örneğin,yük yoğunluğu gibi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Hacim integrali cok degiskenli kalkulusteki cokkatli integralin 3 boyutlu durumudur Hacim integrali fizikte onemli bir yere sahiptir Ozellikle yogunluklarin hesabi icin kullanilir Kartezyen koordinat sistemindeHacim integrali D R3 displaystyle D subset R 3 bolgesinde tanimli f x y z displaystyle f x y z fonksiyonunun anlamina da gelir Su sekilde yazilir Df x y z dxdydz displaystyle iiint limits D f x y z dxdydz Bu integral silindirik koordinat sisteminde soyle yazilir Df p f z pdpdfdz displaystyle iiint limits D f p varphi z pdpd varphi dz Kuresel koordinat sisteminde ise soyle bir yazim mevcuttur Df r 8 f r2sin8drd8df displaystyle iiint limits D f r theta varphi r 2 sin theta drd theta d varphi Ornekf x y z 1 displaystyle f x y z 1 f x y z dx dy dz displaystyle iiint f x y z dx dy dz 1 dx dy dz displaystyle iiint 1 dx dy dz 01dx 01dy 01dz displaystyle int 0 1 dx int 0 1 dy int 0 1 dz 1Fiziktem rdV displaystyle m iiint rho dV Burada m displaystyle m kutle r displaystyle rho kutle yogunlugu birimi kg m 3 Ayni sekilde farkli buyukluklerin yogunlugu alinabilir Ornegin yuk yogunlugu gibi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State