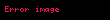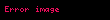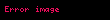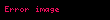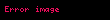Matematikte verilmiş bir P noktasındaki ve V vektörü boyuncaki çok değişkenli bir fonksiyonun yönlü türevi sezgisel olarak fonksiyonun P noktasında, V vektörü boyuncaki anlık değişim oranını temsil eder. Bu yüzden, kısmi türev fikrinin genelleştirmesidir çünkü kısmi türevler alınırken yön her zaman paralel olarak alınmaktadır.
Yönlü türev, özel bir durumudur.
Tanım
Bir 

limiti tarafından verilen fonksiyondur.
Bazı yazarlar 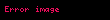

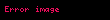
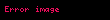
olur. Burada, sağdaki 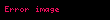

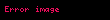


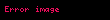
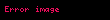
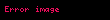
Özellikler
Sırdan türevin birçok özelliği yönlü türev için de geçerlidir. Bunlar, bir p 'nin komşuluğunda tanımlı ve p 'de olan herhangi bir f ve g fonksiyonları için şu özellikleri kapsar:
- :
- : Herhangi bir c sabiti için,
- Çarpma kuralı (veya ):
- Zincir kuralı: Eğer g, p 'de türevlenebilir ise ve h, g(p) 'de türevlenebilir ise, o zaman
Diferansiyel geometri
M, bir ve p, M 'nin noktası olsun. f, p 'nin komşuluğunda tanımlı ve p 'de bir fonksiyon olsun. Eğer v M 'ye p noktasında ise, o zaman f 'nin v boyuncaki yönlü türevi (değişik şekillerde 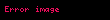
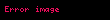

ile tanımlanır. Bu tanımın, γ, γ'(0) = v olacak şekilde seçildiği sürece, γ 'nın seçiminden bağımsız olduğu kanıtlanabilir.
Normal türev
Normal türev, uzaydaki bir yüzeye normal (yani dik) yönde veya daha genel bir şekilde bir dik olan alanı boyunca alınan bir yönlü türevdir. Örnek olarak görünüz. Eğer normal yön 

Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte verilmis bir P noktasindaki ve V vektoru boyuncaki cok degiskenli bir fonksiyonun yonlu turevi sezgisel olarak fonksiyonun P noktasinda V vektoru boyuncaki anlik degisim oranini temsil eder Bu yuzden kismi turev fikrinin genellestirmesidir cunku kismi turevler alinirken yon her zaman paralel olarak alinmaktadir Yonlu turev ozel bir durumudur TanimBir f x f x1 x2 xn displaystyle f vec x f x 1 x 2 ldots x n bir v v1 vn displaystyle vec v v 1 ldots v n vektoru boyuncaki yonlu turevi v f x limh 0f x hv f x h displaystyle nabla vec v f vec x lim h rightarrow 0 frac f vec x h vec v f vec x h limiti tarafindan verilen fonksiyondur Bazi yazarlar v displaystyle nabla v yerine Dv yi de kullanmaktadirlar Eger f displaystyle f fonksiyonu x displaystyle vec x te turevlenebilir ise o zaman yonlu turev herhangi bir v displaystyle vec v vektoru boyunca vardir ve v f x f x v displaystyle nabla vec v f vec x nabla f vec x cdot vec v olur Burada sagdaki displaystyle nabla gradyani displaystyle cdot ise temsil etmektedir Herhangi bir x displaystyle vec x noktasinda f displaystyle f nin yonlu turevi f displaystyle f deki v displaystyle vec v vektoru boyunca x displaystyle vec x noktasindaki degisim oranini temsil etmektedir Yukaridaki tanim her ne kadar herhangi bir vektor hatta sifir vektoru icin tanimli olsa da genelde yonler birimlestirilmis olarak alinir ki boylece v displaystyle vec v birim vektor olur Ozellikler Sirdan turevin bircok ozelligi yonlu turev icin de gecerlidir Bunlar bir p nin komsulugunda tanimli ve p de olan herhangi bir f ve g fonksiyonlari icin su ozellikleri kapsar v f g vf vg displaystyle nabla v f g nabla v f nabla v g Herhangi bir c sabiti icin v cf c vf displaystyle nabla v cf c nabla v f Carpma kurali veya v fg g vf f vg displaystyle nabla v fg g nabla v f f nabla v g Zincir kurali Eger g p de turevlenebilir ise ve h g p de turevlenebilir ise o zaman vh g p h g p vg p displaystyle nabla v h circ g p h g p nabla v g p dd Diferansiyel geometriM bir ve p M nin noktasi olsun f p nin komsulugunda tanimli ve p de bir fonksiyon olsun Eger v M ye p noktasinda ise o zaman f nin v boyuncaki yonlu turevi degisik sekillerde vf p displaystyle nabla v f p Lvf p displaystyle L v f p veya vp f displaystyle v p f olarak da gosterilir su sekilde tanimlanabilir g 1 1 M g 0 p ve g 0 v olan turevlenebilir bir egri olsun O zaman yonlu turev vf p ddtf g t t 0 displaystyle nabla v f p left frac d d tau f circ gamma tau right tau 0 ile tanimlanir Bu tanimin g g 0 v olacak sekilde secildigi surece g nin seciminden bagimsiz oldugu kanitlanabilir Normal turevNormal turev uzaydaki bir yuzeye normal yani dik yonde veya daha genel bir sekilde bir dik olan alani boyunca alinan bir yonlu turevdir Ornek olarak gorunuz Eger normal yon n displaystyle vec n ile gosterilirse o zaman ƒ nin yonlu turevi bazen f n displaystyle frac partial f partial n ile gosterilir Ayrica bakinizKaynakca Bakiniz 1974 Mathematical Analysis Addison Wesley ss 344 345 ISBN 0 201 00288 4
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State