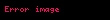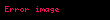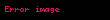Zincir kuralı bir değişkene bağlı bir fonksiyonun değişkeninin başka bir değişkene bağlı olması durumunda türevinin:
şeklinde yazılabilmesidir []. Diğer gösterimleri ise
ve
şeklindedir.
Örnekler
Örnek A
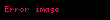
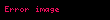
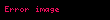
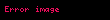
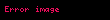
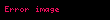
Örnek B
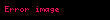
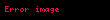
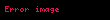
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Zincir kurali bir degiskene bagli bir fonksiyonun degiskeninin baska bir degiskene bagli olmasi durumunda turevinin dfdx dfdu dudx displaystyle frac df dx frac df du cdot frac du dx seklinde yazilabilmesidir u u x displaystyle u u x Diger gosterimleri ise f g x f g x g x displaystyle f circ g x f g x g x ve dfdx ddxf g x f g x g x displaystyle frac df dx frac d dx f g x f g x g x seklindedir OrneklerOrnek A f x sin x3 displaystyle f x sin x 3 ifadesi f x h g x displaystyle f x h g x olarak yazilabilir Burada h x sin x displaystyle h x sin x ve g x x3 displaystyle g x x 3 olarak tanimlidir Zincir kurali uygulanirsa f fonksiyonunun turevi dfdx ddxh g x h g x g x displaystyle frac df dx frac d dx h g x h g x g x olarak yazilabilir Turevler yerine koyulursa dfdx cos x3 3x2 displaystyle frac df dx cos x 3 cdot 3x 2 sonucu bulunur Ornek B f u ln u displaystyle f u ln u ve u sin x displaystyle u sin x olarak verilsin f fonksiyonunun x e gore degisimi zincir kurali ile dfdx dfdu dudx 1ududx cos x sin x cot x displaystyle frac df dx frac df du cdot frac du dx frac 1 u frac du dx frac cos x sin x cot x olarak bulunur
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State