Fizikte ve matematikte, matematikçi Hermann Minkowski anısına adlandırılan Minkowski uzayı veya Minkowski uzayzamanı, Einstein'ın özel görelilik kuramının en uygun biçimde gösterimlendiği matematiksel yapıdır. Bu yapıda, bilinen üç uzay boyutu tek bir zaman boyutuyla birleştirilerek, uzay zamanını betimlemek için dört boyutlu bir çokkatlı oluşturulmuştur.
Kuramsal fizikte, Minkowski uzayı çoğunlukla Öklid uzayıyla karşılaştırılır. Öklid uzayında yalnızca boyutlar varken Minkowski uzayında ayrıca bir zamansal boyut da bulunur. Bu yüzden Öklid uzayının , olup Minkowksi uzayınınki ise Poincaré grubudur.
Minkowski uzayında geometrik uzunluğa karşılık gelen uzayzaman aralığı ya uzaysal ya ışınsal ("yansız") ya da zamansaldır.
Dörtvektörlerde Minkovski iççarpımı
- Ana madde: . Ayrıca vektör ve maddelerine bakınız.
Bir dörtvektör, dört adet koordinat bileşeni olan vektöre denir. Bu maddede dörtvektörler, koyu ve büyük harflerle gösterilecektir; koyu ve küçük harflerle gösterilenler de üçvektörler, yâni bilinen üç boyutlu vektörler olacaktır.
Bilindik oldukça benzeyen, hattâ bilindik iççarpım cinsinden yazılabilen Minkovski iççarpımı, dört boyutlu "hiperbolik" bir iççarpım sunmaktadır. Eğer dörtvektörleri 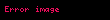

olarak tanımlanabilir. Bilindik iççarpım cinsinden de
biçimini alır. Buradan hareketle bir dörtvektörün boyu da,
olarak bulunur.
Minkovski iççarpımı, kullanılarak da tanımlanabilir. 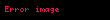

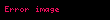
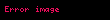
Böylece Minkovski iççarpımı
olarak yazılmış olur. Burada
olarak tanımlandığında iççarpım,
biçimini alır. Bu gösterim genel görelilik kuramı çerçevesinde tensör gösterimlerinde sıkça kullanılmaktadır.
- Daha ilerisi için maddesine bakınız.
Bilinen vektörlerde olanın tersine, dörtvektörlerin boyları çıkabilir. 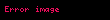
Burada 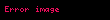
olarak da gösterildiği olur. Burada aynı şekilde 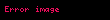
olarak elde edilir.
Dörtkonum
Bilinen şekliyle uzayda vektörler, üç koordinatla gösterilirler: x, y, z. Ancak özel görelilikte ayrıca zaman koordinatı da uzayın, daha doğrusu uzayzamanın bir parçasıdır. Bu yüzden burada vektörler, dört koordinata sahip olurlar. Örneğin bilinen biçimiyle bir konum vektörü,
şeklindedir (Bu maddede küçük kalın harfler, üçvektörleri betimleyecektir). Bu vektör, metre birimindedir. Bu vektöre bir de t koordinatını eklersek birim karmaşası olacağından onun yerine dördüncü koordinat ct olarak alınır. Burada c ışık hızı olduğundan bu koordinat yine metre biriminde olacaktır. O halde bir dörtvektör,
olarak gösterilmiş olur.
Bir dörtkonumun boyu
olarak elde edilir. Burada dörtkonum bir , yâni Lorentz dönüşümleri altında eylemsiz tüm göre değişmezdir. 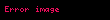
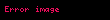
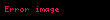
olduğu Lorentz dönüşümleri kullanılarak kolaylıkla gösterilebilir. Bu durum ışık için de geçerlidir ki aslında ışık için dörtkonum doğrudan özel görelilik kuramının ikinci ilkesi olan ışık hızının her gözlemciye göre değişmezliği ilkesini ifâde eder. Eğer ışık her gözlemciye göre sabit hızla gidiyorsa, x=vt ifâdesinden dolayı her iki yönü de kapsayacak şekilde
olarak yazılır. Bu ifâdenin karesi alındığında
olur ve buradan
çıkarsanır. Minkovski uzayzamanında bu türden bir vektöre ışınsı vektör denir. Bu vektörler c ışık hızında giden parçacıkların hareket denklemidir. Herhangi bir gözlemci için
ise, bu tür vektörlere zamansı vektör denir. Bu vektörler, c hızından düşük hızlarda hareket eden gözlemcileri betimler. Yine eğer bir gözlemci için,
oluyorsa (olabildiği, Minkovski iççarpımı altbaşlığında irdelenmişti) bu durumda bu vektörlere uzamsı vektör denir. Bu vektörler de c hızından yüksek hızlardaki gözlemcileri betimler. Bu tür parçacıklara takyon dendiği de olur.
Dörthız
Bilindik biçimiyle bir hız vektörü üç koordinata sahiptir:
Bir hız vektörü, konum vektörünün zamana göre türevi şeklinde tanımlandığına göre, yani 
olduğundan, dörthız vektörü de aynı şekilde dörtkonumun zaman göre türevi olarak tanımlanmalıdır:
Burada 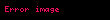
olduğu görülür.
Ayrıca dörthızın boyunun
olduğu görülebilir. Burada
olarak yeniden yazılabilir, o halde dörthız vektörünün,
olduğu görülür.
Dörtmomentum
Momentum, kütle ile hızın çarpımıydı,
Burada da aynı usavurum devam ediyor ancak küçük ayrıntılar oluşmakta:
Burada 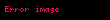
Burada dikkat edilmesi gereken şey, dördüncü koordinatın sadece kütle oluşudur (sonuçta c bir sabit). Bu yüzden dörtmomentumun korunumu aslında Newton fiziğinde "momentumun korunumu" ile "kütlenin korunumu" ilkelerinin ikisini birden kapsar. Böylece iki denklemi
(momentumun korunumu) (kütlenin korunumu)
olarak yazmak yerine,
(4-momentumun korunumu)
gibi tek bir denklem yazılmış olur. Bunun yanı sıra 
O halde dörtmomentumun boyu, yukarıdaki dörthızın boyunda elde edilen sonuç kullanılarak
şeklinde elde edilir. Ayrıca, doğrudan boyladığımızda
olduğundan, bu iki ifâde eşitlenince
ortaya özel göreliliğin en temel denklemlerinden biri olan momentum enerji bağıntısı, yâni
bağıntısı çıkar.
Dörtivme
İvme, hızın zaman göre türevidir. Bilindik ivme
şeklinde idi. Bu durumda dörtivme,
olarak elde edilir (burada 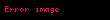
olur. Eğer gözlemciyle aynı ivmeyi inceleyecek olursak, u=0 olacağından
bulunur. O halde, yalnız 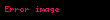

Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte ve matematikte matematikci Hermann Minkowski anisina adlandirilan Minkowski uzayi veya Minkowski uzayzamani Einstein in ozel gorelilik kuraminin en uygun bicimde gosterimlendigi matematiksel yapidir Bu yapida bilinen uc uzay boyutu tek bir zaman boyutuyla birlestirilerek uzay zamanini betimlemek icin dort boyutlu bir cokkatli olusturulmustur Kuramsal fizikte Minkowski uzayi cogunlukla Oklid uzayiyla karsilastirilir Oklid uzayinda yalnizca boyutlar varken Minkowski uzayinda ayrica bir zamansal boyut da bulunur Bu yuzden Oklid uzayinin olup Minkowksi uzayininki ise Poincare grubudur Minkowski uzayinda geometrik uzunluga karsilik gelen uzayzaman araligi ya uzaysal ya isinsal yansiz ya da zamansaldir Dortvektorlerde Minkovski iccarpimiAna madde Ayrica vektor ve maddelerine bakiniz Bir dortvektor dort adet koordinat bileseni olan vektore denir Bu maddede dortvektorler koyu ve buyuk harflerle gosterilecektir koyu ve kucuk harflerle gosterilenler de ucvektorler yani bilinen uc boyutlu vektorler olacaktir Bilindik oldukca benzeyen hatta bilindik iccarpim cinsinden yazilabilen Minkovski iccarpimi dort boyutlu hiperbolik bir iccarpim sunmaktadir Eger dortvektorleri V v0 v1 v2 v3 displaystyle scriptstyle mathbf V v 0 v 1 v 2 v 3 ve W w0 w1 w2 w3 displaystyle scriptstyle mathbf W w 0 w 1 w 2 w 3 olarak secersek Minkovski iccarpimi bilesenler cinsinden V W v0w0 v1w1 v2w2 v3w3 displaystyle langle mathbf V mathbf W rangle v 0 w 0 v 1 w 1 v 2 w 2 v 3 w 3 olarak tanimlanabilir Bilindik iccarpim cinsinden de V W v0w0 v w displaystyle langle mathbf V mathbf W rangle v 0 w 0 mathbf v cdot mathbf w bicimini alir Buradan hareketle bir dortvektorun boyu da V V displaystyle langle mathbf V mathbf V rangle displaystyle V2 displaystyle mathbf V 2 displaystyle v02 v12 v22 v32 displaystyle v 0 2 v 1 2 v 2 2 v 3 2 displaystyle v02 v2 displaystyle v 0 2 mathbf v 2 olarak bulunur Minkovski iccarpimi kullanilarak da tanimlanabilir em displaystyle scriptstyle e mu ifadesi birim vektorlerin m 0 1 2 3 displaystyle scriptstyle mu 0 1 2 3 olan bilesenlerini ifade edecek sekilde her dortvektor V emVm displaystyle scriptstyle mathbf V e mu V mu ve W enWn displaystyle scriptstyle mathbf W e nu W nu olarak yazilabilir Burada birim vektorlerin Minkovski iccarpimlari Minkovski metriginin birim ogesine esit olarak tanimlanir em en hmn 10000 10000 10000 1 displaystyle langle e mu e nu rangle eta mu nu begin bmatrix 1 amp amp 0 amp amp 0 amp amp 0 0 amp amp 1 amp amp 0 amp amp 0 0 amp amp 0 amp amp 1 amp amp 0 0 amp amp 0 amp amp 0 amp amp 1 end bmatrix Boylece Minkovski iccarpimi V W hmnvmwn displaystyle langle mathbf V mathbf W rangle eta mu nu v mu w nu olarak yazilmis olur Burada vn hmnvm displaystyle v nu eta mu nu v mu olarak tanimlandiginda iccarpim V W vnwn displaystyle langle mathbf V mathbf W rangle v nu w nu bicimini alir Bu gosterim genel gorelilik kurami cercevesinde tensor gosterimlerinde sikca kullanilmaktadir Daha ilerisi icin maddesine bakiniz Bilinen vektorlerde olanin tersine dortvektorlerin boylari cikabilir v02 lt v2 displaystyle scriptstyle v 0 2 lt mathbf v 2 oldugu zaman dortvektorun boyu sifirdan kucuk olacaktir Bu durum hiperbolik sayilarda da boyle oldugundan bazen dortvektorler sayilarla da ifade edilir z v0 v1i v2j v3k displaystyle z v 0 v 1 hat mathbf i v 2 hat mathbf j v 3 hat mathbf k Burada i2 j2 k2 ijk 1 displaystyle scriptstyle mathbf i 2 mathbf j 2 mathbf k 2 mathbf ijk 1 olarak tanimlanan ve hicbiri 1e esit olmayan sayilardir Dortvektorun boyu yine ayni kalir Bazen sadece z v0 hv displaystyle z v 0 mathbf h mathbf v olarak da gosterildigi olur Burada ayni sekilde h2 1 displaystyle scriptstyle mathbf h 2 1 olarak tanimlanir Bu durumda dortvektorun boyu z 2 zz v0 hv v0 hv v02 h2v2 v02 v2 displaystyle z 2 zz v 0 mathbf hv v 0 mathbf hv v 0 2 mathbf h 2 mathbf v 2 v 0 2 mathbf v 2 olarak elde edilir DortkonumBilinen sekliyle uzayda vektorler uc koordinatla gosterilirler x y z Ancak ozel gorelilikte ayrica zaman koordinati da uzayin daha dogrusu uzayzamanin bir parcasidir Bu yuzden burada vektorler dort koordinata sahip olurlar Ornegin bilinen bicimiyle bir konum vektoru r x y z displaystyle mathbf r x y z seklindedir Bu maddede kucuk kalin harfler ucvektorleri betimleyecektir Bu vektor metre birimindedir Bu vektore bir de t koordinatini eklersek birim karmasasi olacagindan onun yerine dorduncu koordinat ct olarak alinir Burada c isik hizi oldugundan bu koordinat yine metre biriminde olacaktir O halde bir dortvektor R ct r ct x y z displaystyle mathbf R ct mathbf r ct x y z olarak gosterilmis olur Bir dortkonumun boyu R2 c2t2 x2 y2 z2 displaystyle mathbf R 2 c 2 t 2 x 2 y 2 z 2 olarak elde edilir Burada dortkonum bir yani Lorentz donusumleri altinda eylemsiz tum gore degismezdir R displaystyle scriptstyle mathbf R dortkonumu bir S basvuru cercevesindeki gozlemcinin uzayzamandaki konumunu ve R displaystyle scriptstyle mathbf R dortkonumu da S ye gore sabit u hizinda hareket eden bir baska S displaystyle scriptstyle S cercevesindeki gozlemcinin uzayzamandaki konumunu ifade etsin O halde R2 R 2 displaystyle mathbf R 2 mathbf R 2 oldugu Lorentz donusumleri kullanilarak kolaylikla gosterilebilir Bu durum isik icin de gecerlidir ki aslinda isik icin dortkonum dogrudan ozel gorelilik kuraminin ikinci ilkesi olan isik hizinin her gozlemciye gore degismezligi ilkesini ifade eder Eger isik her gozlemciye gore sabit hizla gidiyorsa x vt ifadesinden dolayi her iki yonu de kapsayacak sekilde r ct displaystyle mathbf r pm ct olarak yazilir Bu ifadenin karesi alindiginda r2 c2t2 displaystyle mathbf r 2 c 2 t 2 olur ve buradan c2t2 x2 y2 z2 0 displaystyle c 2 t 2 x 2 y 2 z 2 0 R2 0 displaystyle mathbf R 2 0 cikarsanir Minkovski uzayzamaninda bu turden bir vektore isinsi vektor denir Bu vektorler c isik hizinda giden parcaciklarin hareket denklemidir Herhangi bir gozlemci icin R2 gt 0 displaystyle mathbf R 2 gt 0 ise bu tur vektorlere zamansi vektor denir Bu vektorler c hizindan dusuk hizlarda hareket eden gozlemcileri betimler Yine eger bir gozlemci icin R2 lt 0 displaystyle mathbf R 2 lt 0 oluyorsa olabildigi Minkovski iccarpimi altbasliginda irdelenmisti bu durumda bu vektorlere uzamsi vektor denir Bu vektorler de c hizindan yuksek hizlardaki gozlemcileri betimler Bu tur parcaciklara takyon dendigi de olur DorthizBilindik bicimiyle bir hiz vektoru uc koordinata sahiptir u ux uy uz displaystyle mathbf u u x u y u z Bir hiz vektoru konum vektorunun zamana gore turevi seklinde tanimlandigina gore yani t displaystyle tau olmak uzere u drdt displaystyle mathbf u d mathbf r over d tau oldugundan dorthiz vektoru de ayni sekilde dortkonumun zaman gore turevi olarak tanimlanmalidir U dRdt cdtdt dxdt dydt dzdt displaystyle mathbf U d mathbf R over d tau left frac cdt d tau frac dx d tau frac dy d tau frac dz d tau right Burada dt gdt displaystyle dt gamma d tau oldugundan U gc gux guy guz g c uz uy uz g c u displaystyle mathbf U gamma c gamma u x gamma u y gamma u z gamma c u z u y u z gamma c mathbf u oldugu gorulur Ayrica dorthizin boyunun U2 displaystyle mathbf U 2 displaystyle hmnUmUn displaystyle eta mu nu U mu U nu displaystyle g2c2 g2 ux2 uy2 uz2 displaystyle gamma 2 c 2 gamma 2 u x 2 u y 2 u z 2 displaystyle g2 c2 u2 displaystyle gamma 2 c 2 mathbf u 2 oldugu gorulebilir Burada g2 11 u2c2 1c2 u2c2 c2c2 u2 displaystyle gamma 2 1 over 1 frac mathbf u 2 c 2 1 over frac c 2 mathbf u 2 c 2 c 2 over c 2 mathbf u 2 olarak yeniden yazilabilir o halde dorthiz vektorunun U2 c2 displaystyle mathbf U 2 c 2 oldugu gorulur DortmomentumMomentum kutle ile hizin carpimiydi p gm0u px py pz displaystyle mathbf p gamma m 0 mathbf u p x p y p z Burada da ayni usavurum devam ediyor ancak kucuk ayrintilar olusmakta P m0U gm0 c ux uy uz m c ux uy uz mc px py pz displaystyle mathbf P m 0 mathbf U gamma m 0 c u x u y u z m c u x u y u z mc p x p y p z Burada m0 displaystyle m 0 durgun kutle ve m goreli kutledir Burada dikkat edilmesi gereken sey dorduncu koordinatin sadece kutle olusudur sonucta c bir sabit Bu yuzden dortmomentumun korunumu aslinda Newton fiziginde momentumun korunumu ile kutlenin korunumu ilkelerinin ikisini birden kapsar Boylece iki denklemi p1 p2 p1 p2 displaystyle mathbf p 1 mathbf p 2 mathbf p 1 mathbf p 2 momentumun korunumu m1 m2 m1 m2 displaystyle m 1 m 2 m 1 m 2 kutlenin korunumu olarak yazmak yerine P1 P2 P1 P2 displaystyle mathbf P 1 mathbf P 2 mathbf P 1 mathbf P 2 4 momentumun korunumu gibi tek bir denklem yazilmis olur Bunun yani sira E mc2 displaystyle scriptstyle E mc 2 oldugundan aslinda bu enerjinin de korunumudur ve dortmomentumun dorduncu bilesenini enerji yapar P E c p displaystyle mathbf P E c mathbf p O halde dortmomentumun boyu yukaridaki dorthizin boyunda elde edilen sonuc kullanilarak P2 displaystyle mathbf P 2 displaystyle m02U2 displaystyle m 0 2 mathbf U 2 displaystyle m02c2 displaystyle m 0 2 c 2 seklinde elde edilir Ayrica dogrudan boyladigimizda P2 displaystyle mathbf P 2 displaystyle m2c2 px2 py2 pz2 displaystyle m 2 c 2 p x 2 p y 2 p z 2 displaystyle m2c2 p2 displaystyle m 2 c 2 mathbf p 2 displaystyle E2 c2 p2 displaystyle E 2 c 2 mathbf p 2 oldugundan bu iki ifade esitlenince m02c2 E2 c2 p2 displaystyle m 0 2 c 2 E 2 c 2 mathbf p 2 m02c4 E2 p2c2 displaystyle m 0 2 c 4 E 2 mathbf p 2 c 2 E02 E2 p2c2 displaystyle E 0 2 E 2 mathbf p 2 c 2 ortaya ozel goreliligin en temel denklemlerinden biri olan momentum enerji bagintisi yani E2 p2c2 E02 displaystyle E 2 mathbf p 2 c 2 E 0 2 bagintisi cikar DortivmeIvme hizin zaman gore turevidir Bilindik ivme a dudt ax ay az displaystyle mathbf a d mathbf u over d tau a x a y a z seklinde idi Bu durumda dortivme A displaystyle mathbf A displaystyle dUdt displaystyle d mathbf U over d tau displaystyle cdgdt d gu dt displaystyle left c frac d gamma d tau d gamma mathbf u over d tau right displaystyle cdgdt udgdt ga displaystyle left c frac d gamma d tau mathbf u frac d gamma d tau gamma mathbf a right displaystyle g3 u ac a displaystyle gamma 3 left frac mathbf u cdot mathbf a c mathbf a right olarak elde edilir burada a displaystyle mathbf a Bu ifadedeki 4 bilesen hizla ivmenin nokta carpimidir Bu carpim sifir olur yani A g3 0 a displaystyle mathbf A gamma 3 0 mathbf a olur Eger gozlemciyle ayni ivmeyi inceleyecek olursak u 0 olacagindan A 0 a displaystyle mathbf A 0 mathbf a bulunur O halde yalniz a 0 displaystyle scriptstyle mathbf a 0 oldugunda dortivme A 0 displaystyle scriptstyle mathbf A 0 olacaktir Oysa u 0 displaystyle scriptstyle mathbf u 0 olsa bile dorthiz sifirlanmiyordu Kaynakca
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State