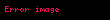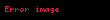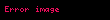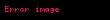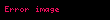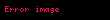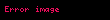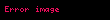Matematikte Öklid uzayı, Öklid geometrisinin üç boyutlu uzayıdır ve bu kavramlar, çok boyutlu olarak genelleştirilir. “Öklid” terimi bu uzayları, Öklid geometrisi olmayan eğimli uzaydan ve Einstein'nın genel görelilik kuramından ayırt eder. Bu adı Yunan matematikçi Öklid'den dolayı almıştır.

Modern matematikte Öklid uzayını ifade etmek için kartezyen koordinat sistemi ve analitik geometri kavramları çok yaygın olarak kullanılır.
Reel koordinat uzayı
Reel sayılar kümesi R ile gösterilsin. Herhangi bir pozitif n tamsayısı. Rde n boyutlu vektör uzayında tüm n katlı reel sayılardan oluşsun. Bu Rn sembolü ile gösterilir ve bazen reel koordinat uzayı olarak adlandırılır. Rnde bir eleman şöyle yazılabilir;
Her bir xi, bir reel sayıdır. Rndeki vektör uzayı işlemleri şöyle ifade edilir;
Rn vektör uzayı doğal taban ile gösterilir:
Rnde keyfi bir vektör, aşağıdaki biçimde yazılabilir;
Rn, bir n boyutlu vektör uzayında prototip örnektir. Aslında her reel n boyutlu vektör uzayı V, Rnizomorfizmasıdır.
Öklid yapısı
Öklid uzayı, bir reel koordinat uzayında daha fazlasıdır. Öklid geometrisinde işlem yapmak için noktalar arasındaki mesafeden ve çizgi veya vektörler arasındaki açıdan da bahsetmek gerekir. Bu nicelikleri elde etmenin doğal yolu, Rn'de nokta çarpım kullanmak gerekir. Herhangi x ve y iki reel nvektörü nokta çarpımı şöyle ifade edilir;
Sonuç daima bir reel sayıdır. Ayrıca xin kendisi ile nokta çarpımı hiçbir zaman negatif olmaz. Bu çarpım, bir x vektörünün "uzunluğunu" ifade etmemizi sağlar, şöyle ki;
Bu uzunluk fonksiyonu, gerekli norm özelliğini sağlar ve Rnde Öklid normu olarak adlandırılır.
θ (0° ≤ θ ≤ 180°), x ile y arasındaki sabit açıdır (periyodik olmayan) ve şöyle ifade edilir;
burada cos−1, arccos'un ters trigonometrik fonksiyonudur.
Son olarak, Rndeki bir metriği (uzaklık fonksiyonunu) ifade etmek için aşağıdaki norm kullanılabilir;
Bu uzaklık fonksiyonu Öklid uzaklığı olarak adlandırılır ve Pisagor teoreminin bir biçimi olarak görülebilir.
Reel koordinat uzayı ile bu Öklid yapısı Öklid uzayı olarak adlandırılır ve daha çok En sembolü ile gösterilir. (Çoğu yazar, Öklid uzayında çalışırken Öklid yapısının anlaşılması için Rn sembolünü kullanmayı tercih eder).
T doğrusal dönüşümlerine yönelimi ifade etmek için Öklid uzayı dönüşü (rotasyonu) kullanılır. Bunlar açı ve uzaklıkla belirtilir;
Matrisde dönüş, özel ortogonal matrislerdir.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Oklid uzayi Oklid geometrisinin uc boyutlu uzayidir ve bu kavramlar cok boyutlu olarak genellestirilir Oklid terimi bu uzaylari Oklid geometrisi olmayan egimli uzaydan ve Einstein nin genel gorelilik kuramindan ayirt eder Bu adi Yunan matematikci Oklid den dolayi almistir Uc boyutlu Oklid uzayindaki her bir nokta uc koordinat ile ifade edilir Modern matematikte Oklid uzayini ifade etmek icin kartezyen koordinat sistemi ve analitik geometri kavramlari cok yaygin olarak kullanilir Reel koordinat uzayiReel sayilar kumesi R ile gosterilsin Herhangi bir pozitif n tamsayisi Rde n boyutlu vektor uzayinda tum n katli reel sayilardan olussun Bu Rn sembolu ile gosterilir ve bazen reel koordinat uzayi olarak adlandirilir Rnde bir eleman soyle yazilabilir x x1 x2 xn displaystyle mathbf x x 1 x 2 ldots x n Her bir xi bir reel sayidir Rndeki vektor uzayi islemleri soyle ifade edilir x y x1 y1 x2 y2 xn yn displaystyle mathbf x mathbf y x 1 y 1 x 2 y 2 ldots x n y n ax ax1 ax2 axn displaystyle a mathbf x ax 1 ax 2 ldots ax n Rn vektor uzayi dogal taban ile gosterilir e1 1 0 0 e2 0 1 0 en 0 0 1 displaystyle begin aligned mathbf e 1 amp 1 0 ldots 0 mathbf e 2 amp 0 1 ldots 0 amp vdots mathbf e n amp 0 0 ldots 1 end aligned Rnde keyfi bir vektor asagidaki bicimde yazilabilir x i 1nxiei displaystyle mathbf x sum i 1 n x i mathbf e i Rn bir n boyutlu vektor uzayinda prototip ornektir Aslinda her reel n boyutlu vektor uzayi V Rnizomorfizmasidir Oklid yapisiOklid uzayi bir reel koordinat uzayinda daha fazlasidir Oklid geometrisinde islem yapmak icin noktalar arasindaki mesafeden ve cizgi veya vektorler arasindaki acidan da bahsetmek gerekir Bu nicelikleri elde etmenin dogal yolu Rn de nokta carpim kullanmak gerekir Herhangi x ve y iki reel nvektoru nokta carpimi soyle ifade edilir x y i 1nxiyi x1y1 x2y2 xnyn displaystyle mathbf x cdot mathbf y sum i 1 n x i y i x 1 y 1 x 2 y 2 cdots x n y n Sonuc daima bir reel sayidir Ayrica xin kendisi ile nokta carpimi hicbir zaman negatif olmaz Bu carpim bir x vektorunun uzunlugunu ifade etmemizi saglar soyle ki x x x i 1n xi 2 displaystyle mathbf x sqrt mathbf x cdot mathbf x sqrt sum i 1 n x i 2 Bu uzunluk fonksiyonu gerekli norm ozelligini saglar ve Rnde Oklid normu olarak adlandirilir 8 0 8 180 x ile y arasindaki sabit acidir periyodik olmayan ve soyle ifade edilir 8 cos 1 x y x y displaystyle theta cos 1 left frac mathbf x cdot mathbf y mathbf x mathbf y right burada cos 1 arccos un ters trigonometrik fonksiyonudur Son olarak Rndeki bir metrigi uzaklik fonksiyonunu ifade etmek icin asagidaki norm kullanilabilir d x y x y i 1n xi yi 2 displaystyle d mathbf x mathbf y mathbf x mathbf y sqrt sum i 1 n x i y i 2 Bu uzaklik fonksiyonu Oklid uzakligi olarak adlandirilir ve Pisagor teoreminin bir bicimi olarak gorulebilir Reel koordinat uzayi ile bu Oklid yapisi Oklid uzayi olarak adlandirilir ve daha cok En sembolu ile gosterilir Cogu yazar Oklid uzayinda calisirken Oklid yapisinin anlasilmasi icin Rn sembolunu kullanmayi tercih eder T dogrusal donusumlerine yonelimi ifade etmek icin Oklid uzayi donusu rotasyonu kullanilir Bunlar aci ve uzaklikla belirtilir Tx Ty x y displaystyle T mathbf x cdot T mathbf y mathbf x cdot mathbf y Tx x displaystyle T mathbf x mathbf x Matrisde donus ozel ortogonal matrislerdir Ayrica bakinizKartezyen koordinat sistemi Kutupsal koordinat sistemi Hilbert uzayi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State