Bu madde veya sayfa başka bir dilden kötü bir biçimde tercüme edilmiştir. Sayfa makine çevirisi veya dilde yetkinliği bulunmayan bir çevirmen tarafından oluşturulmuş olabilir. (Temmuz 2022) |
Gök mekaniği olarak, Kepler yörüngesi (veya Keplersel yörünge) üç boyutlu uzayda iki boyutlu bir yörünge düzlemi oluşturan bir elips, parabol, hiperbol benzeri bir yörünge cismininin hareketini açıklar. (Kepler yörüngesi aynı zamanda düz bir çizgi de çizebilir). Kepler yörüngesi yalnızca nokta iki cismin nokta benzeri yerçekimsel çekimlerini dikkate alır, atmosfer sürüklemesi, güneş radyasyonu baskısı, dairesel olmayan cisim merkezi ve bunun gibi bir takım şeylerin diğer cisimlerle girdiği çekim ilişkileri nedeniyle ihmal eder. Böylece Kepler problemi olarak bilinen iki-cisim probleminin, özel durumlara bir çözüm olarak atfedilir. Klasik mekaniğin bir teorisi olarak, aynı zamanda genel görelilik etkilerini dikkate almaz. Kepler yörüngeleri çeşitli şekillerde altı yörünge unsurları içine parametrize edilebilir.

Çoğu uygulamalarda, tüm sistemin kütle merkezi olarak kabul edilen büyük bir merkezi cisim ve kütle merkezi vardır. Ayrıştırma yapılınca, iki objenin benzer kütleleri, ikisinin ortak kütle merkezinin Kepler yörüngesi ya da barisentileri olarak açıklanabilir.
Giriş
Eski çağlardan itibaren 16. ve 17. yüzyıllara kadar gezegenlerin hareketlerinin Antik Yunan filozofları Aristo ve Batlamyus tarafından öğretildiği gibi mükemmel dairesel jeosentrik yolları takip ettiğine inanılırdı. Gezegenlerin hareketler değişimleri (epidaire) üst üste küçük dairesel yollar şeklinde açıklanmıştır.. Gezegenlerin ölçümleri giderek daha kesin olmaya başladığında, bu teoriye revizyonlar önerilmiştir. Hala gezegenlerin güneş merkezli mükemmel dairesel yörüngede gittiğine inanılmasına rağmen 1543 yılında Nicolaus Copernicus, güneş sisteminin bir güneş merkezli modelini yayınladı.
Yasaların geliştirilmesi
1601 yılında Johannes Kepler, Tycho Brahe tarafından yapılan gezegenlerin kapsamlı ve titiz gözlemlerini elde etti. Kepler, sonraki beş yılı Mars gezegeninin gözlemlerini çeşitli eğrilere uydurmaya çalışarak geçirecekti. 1609 yılında Kepler, gezegensel hareketin üç yasasından ilk ikisini yayınladı. Birinci yasa şöyledir:
- "Güneş sistemindeki bütün gezegenler, odaklarının birinde Güneş olan elips şeklindeki bir yörüngede hareket ederler."
Daha genel anlatımla, Kepler hareketini yapan bir nesnenin yolu elips olduğu kadar, parabol veya hiperbol de olabilir. Bu bir grup şekil konik kesitler olarak bilinir. Matematiksel olarak, merkezi bir cisim ile yörüngedeki bir cisim arasındaki mesafe şu şekilde ifade edilebilir:
mesafedir
yörüngenin boyutunu tanımlayan yarı büyük eksendir
yörüngenin şeklini tanımlayan dış merkezliktir
yörüngedeki nesnenin mevcut konumu ile yörüngedeki merkez cisme en yakın olduğu (enberi noktası olarak adlandırılan) konum arasındaki açı olan .
Alternatif olarak, denklem şu şekilde ifade edilebilir:
Burada 
Bu yasaları gözlemleriyle geliştiren Kepler, hiçbir zaman bu hareketleri açıklayacak bir teori geliştirememiştir.
Isaac Newton
Isaac Newton, 1665 ve 1666 yılları arasında hareket, kütleçekim ve diferansiyel hesap ile ilgili çeşitli kavramlar geliştirdi. Bununla birlikte bu kavramlar, 1687 yılında hareket yasalarını ve evrensel kütleçekim yasasını ana hatlarıyla belirttiği Principia'ya kadar yayınlanmadı. Üç hareket yasasından ikincisi şöyle der:
Bir cismin ivmesi, cisme etki eden net kuvvetle paralel ve doğru orantılıdır. Net kuvvet yönündedir ve cismin kütlesi ile ters orantılıdır:
kuvvet vektörüdür
kuvvetin etki ettiği cismin kütlesidir
ivme vektörüdür,
konum vektörünün ikinci zaman türevidir.
Kurallara bakılırsa, denklemin bu şekli yalnızca aşağıda yapılan basitleştirici varsayımlara dayalı olarak doğru olan sabit kütleli bir nesne için geçerlidir.

Newton'un kütleçekim yasası şöyle der:
Her nokta kütle, her iki noktayı kesen doğru boyunca işaret edilen bir kuvvetle diğer nokta kütleleri çeker. Kuvvet, iki kütlenin çarpımı ile orantılı ve nokta kütleler arasındaki uzaklığın karesi ile ters orantılıdır:
iki nokta kütlesi arasındaki kütleçekim kuvvetinin büyüklüğüdür.
kütle çekimi sabitidir
birinci nokta kütlesinin kütlesidir
ikinci nokta kütlesinin kütlesidir
iki nokta kütlesi arasındaki mesafedir
Newton, hareket yasaları ve evrensel kütleçekim yasasından astronomide yörünge hareketine özgü Kepler yasalarını türetebildi. Kepler yasaları gözlem verileriyle iyi bir şekilde desteklendiğinden, bu tutarlılık Newton'un genelleştirilmiş teorisinin ve birleşik göksel ve sıradan mekaniğin geçerliliğine güçlü bir destek sağladı. Bu hareket yasaları, 20. yüzyılın başlarında Albert Einstein özel ve genel görelilik kavramlarını ortaya koyana kadar modern gök mekaniğinin temelini oluşturdu. Çoğu kullanımda Kepler hareketi, gezegenlerin ve uyduların hareketlerini nispeten yüksek doğruluk derecelerine yaklaştırır ve astronomi ve astrodinamikte yaygın olarak kullanılır.
Sadeleştirilmiş iki cisim problemi
İki cisimli bir sistemde bir cismin hareketini çözmek için iki sadeleştirici varsayım yapılabilir:
- Cisimler küresel olarak simetriktir ve nokta kütleler olarak ele alınabilir.
- Cisimlere karşılıklı kütleçekimi dışında etki eden iç ve dış kuvvetler yoktur.
Büyük gök cisimlerinin şekilleri kürelere yakındır. Simetri ile, bir kütle noktasını homojen bir küreye doğru çeken net kütleçekim kuvveti, merkeze doğru yönlenmelidir. (Isaac Newton tarafından da kanıtlanmış olan), kürenin yoğunluğu derinliğe göre değişse bile (çoğu gök cisimleri için olduğu gibi) bu kuvvetin büyüklüğünün, kütlenin tamamı kürenin ortasında toplanmış gibi aynı olduğunu belirtir. Bundan hemen sonra iki homojen küre arasındaki çekim, her ikisinin de kütlesi merkezinde yoğunlaşmış gibidir.
Asteroitler veya uzay araçları gibi daha küçük nesneler genellikle bir küreden güçlü bir şekilde ayrılan bir şekle sahiptir. Ancak bu düzensizlikler tarafından üretilen kütleçekim kuvvetleri, merkezi cismin kütleçekimi ile karşılaştırıldığında genellikle önemsizdir. Düzensiz bir şekil ile mükemmel bir küre arasındaki fark da mesafelerle azalır ve yörünge mesafelerinin çoğu, yörüngedeki küçük bir cismin çapıyla karşılaştırıldığında çok büyüktür. Bu nedenle bazı durumlar için şekil düzensizliği, kesinlik üzerinde önemli bir etki olmaksızın ihmal edilebilir. Bu etki, özellikle alçak yörüngelerde bulunan yapay Dünya uyduları için oldukça belirgindir.
Gezegenler değişen hızlarda dönerler ve bu merkezkaç kuvveti nedeniyle hafif basık bir şekil alabilirler. Böyle yassı bir şekille kütle çekimi, homojen bir küreninkinden bir miktar sapacaktır. Daha büyük mesafelerde bu yassılığın etkisi ihmal edilebilir hale gelir. Güneş Sistemindeki gezegensel hareketler, nokta kütleler olarak ele alınırsa yeterli hassasiyetle hesaplanabilirler.
Kütleleri 
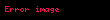


burada 


Kendi kütlelerine bölmek ve ikinci denklemi birinciden çıkarmak, birinci cismin ikinciye göre ivmesi için hareket denklemini verir:
-
(1)

Birçok uygulamada, üçüncü bir sadeleştirici varsayım yapılabilir:
Bu varsayım, sadeleştirilmiş iki cisim problemini çözmek için gerekli değildir, ancak özellikle Dünya yörüngesindeki uydular ve Güneş'in yörüngesindeki gezegenlerle ilgili hesaplamaları basitleştirir. Jüpiter'in kütlesi bile Güneş'inkinden 1047 kat daha azdır, bu da α değerinde %0,096'lık bir hata oluşturur. Dikkate değer istisnalar arasında Dünya-Ay sistemi (kütle oranı 81,3), Plüton-Charon sistemi (kütle oranı 8,9) ve ikili yıldız sistemleri sayılabilir.
Bu varsayımlar altında iki cisim problemi için diferansiyel denklem matematiksel olarak tamamen çözülebilir ve Kepler'in gezegensel hareket yasalarını takip ederek sonuçta oluşan yörüngeye "Kepler yörüngesi" denir. Tüm gezegenlerin yörüngeleri yüksek doğrulukta Güneş etrafındaki Kepler yörüngeleridir. Küçük sapmalar, gezegenler arasındaki çok daha zayıf kütleçekim etkilerinden ve Merkür durumunda genel görelilikten kaynaklanmaktadır. Dünya etrafındaki yapay uyduların yörüngeleri, makul bir tahminle Güneş, Ay ve Dünya'nın yassılığından dolayı küçük düzensizliklere sahip Kepler yörüngeleridir. Hareket denkleminin bütün kütleçekim ve kütleçekim olmayan kuvvetlerin (güneş radyasyon basıncı ve atmosfer direnci gibi) hesaba katılmasıyla sayısal olarak entegre edilmesi gereken yüksek doğruluktaki kullanımlarda, Kepler yörünge kavramları çok önemlidir ve yoğun olarak kullanılır.
Kepler yörünge öğeleri

Kepler yörüngesinin altı parametre ile tanımlanabilirliğinden söz etmek gerekir. Üç boyutlu uzayda hareket eden bir nesnenin hareket bir konum vektörü ve bir hız vektörü ile karakterize edilir. Her vektörün üç bileşeni vardır, bu yüzden uzayda bir yörünge tanımlamak için gerekli değerlerin toplam sayısı altıdır. Bir yörünge (Kepler Elementleri olarak bilinen) ve pozisyon ve hızına bağlı olarak ölçülebilen altı elementten oluşur ki bunların üçü daha önce gösterilmiştir. Bu altı uygun elementten beş tanesi yörünge için değişmezdir. (iki sürekli değişen vektöre bir tezat niteliğinde olmak üzere). Kendi yörüngesinde içindeki bir nesnenin gelecekteki konumu tahmin edilebilir ve yeni konum ve hız kolayca yörünge elemanları ile elde edilebilir.
Bunlardan ikisi eksenin boyutunu ve şeklin belirler:
- Yarımajör eksen (
)
- eksantriklik (
)
Üç tanesi yörünge alanının oryantasyonunu belirler:
- eğim (
)yörünge düzlemi ile referans düzlemi arasındaki açıyı tanımlar.
- Yükselen nodun uzunluğu (
) Referans yönü ve referans düzlemi üzerinde yörüngeye yukarı kesişme (yükselen nod) arasındaki açıyı tanımlar.
- Periapsis argüman(
) artan nod ve periapsis arasındaki açıyı belirler.
Ve son olarak:
- Gerçek anomali (
)periapsis ölçülen yörünge boyunca yörüngedeki cismin konumunu tanımlar. Çeşitli başka değerlerin yerine gerçek bir anomali kullanılabilir, bunlardan en sık kullanılanları mean anomoli olan
ve periapsisden yana geçen süre olan
’dir.



Yukarıdaki diferansiyel denklemin (1) matematiksel çözümü
Herhangi bir merkez kuvveti altında yani r bir kuvvet paraleli ve hareket için, belirli bağıl açısal momentumu 
Pozisyonun çapraz ürünü vektör ve onun hızı olduğu için sabit kaldığından, aynı düzelmde bulunmak zorundadırlar. (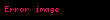





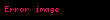
Şimdi vektör 
(Vektör calculusunu inceleyiz). Bunları yerine yazarsak şunu buluruz:
(1)
Bu sıradan olmayan polar diferansiyel denklem verir:
-
(2)
Bu denklemi çözmek için, öncelikle her zaman diferansiyel lineerini ortadan kaldırmak gerekir. Şuna ulaşırız:

-
(3)
(3)’ün zaman diferansiyalinii aldığımız zaman, şuna ulaşırız:
-
(4)
(3) ve (4}) denklemleri ’ın diferansiyellerini elememize izin verir.. In order to eliminate the time derivatives of 
-
(5)
-
(6)

-
(7)
Diferansiyel denklem (7) değişken değişimi ile analitik çözülebilir
-
(8)
Bu verilenleri kullanarak, in (2)’deki tüm zaman diferansiyelleri yoksayılabilir ve bizi 

-
(10)
(10) ve (9)’da belirtilenleri 

-
(11)
genel bir sonuca ulaşılır.
-
(12)
e ve 


Alternatif türevi
Bu denklemi polar diferansiyel denklemini kullanmadan çözmenin bir diğer yolu şöyledir:


Şimdi şunu değerlendiriniz
(Üçlü vektör ürünü). Şunu dikkate alınız
Bu verileri bir önceki denkleme yerleştirdiğimizde
İki tarafın da integralini alırsak
Burada c sabit vektördür. Bunu r' ile birleştirmek ortaya ilginç bir sonuç çıkarır
Burada 


Dikkat ediniz ki 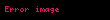
-
(13)
Bu fokal noktada merkezi olan bir konik bölmenin polar koordinatlarının denklemidir. 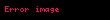
Yörünge denkleminin özellikleri


-
(14)
-
(15)



-
(16)
-
(17)
Sonraki görsel, bir elipsi (kırmızı), bir paraboolü (yeşil) ve bir hiperbolü (mavi) gösterir.

Yatay çizgi üzerinde nokta odak noktasından sağa doğru çıkıyorsa nokta 

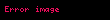
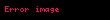
Bir parabol için aralık;
Diferansiyelin zinci kuralını kullanarak (5), (2) denklemi ve p’nin tanımı 
-
(18)
ve teğetsel bileşen olan (hız bileşeni 
-
(19)
Polar argümanı 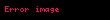
Elips şeklindeki bir yörünge için, dış merkezli anomali olan E’ye geçeriz ve burdan
-
(20)
-
(21)
ve sonuç olarak.
-
(22)
-
(23)
açısal momentum H olmak üzere
-
(24)
Zamana göre entegrasyon olan t ile şu sonuca ulaşılır.
-
(25)
zaman varsayımını yaparak integral sabiti 0 olur. p nin tanımı gereği
-
(26)
şu şekilde yazılabiir
-
(27)
Hiperbolik bir yörünge için parametre yaratmak için hiperbolik fonksiyon kullanılır.
-
(28)
-
(29)
bu durumda şuna ulaşılır
-
(30)
-
(31)
açısal momentum H olmak üzere
-
(32)
Zamana göre entegrasyon olan t ile şu sonuca ulaşılır.
-
(33)
örneğin
-
(34)
t’nin hangi zamanda belirli bir gerçek anomaliye (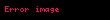
Dikkat ediniz ki (27) ve (34) bu aralıkta bir yer belirler. 
Bazı ilave formüller
Ayrıca bakınız: Merkez denklemi - analitik açılımlar
(20)ve (21)’den edilinen elips yörünge için
-
(35)
ve buna göre
-
(36)
(36)’dan devam ettiğimizde şu sonuç çıkar
Dış merkezli anomalinin geometrik yapısını belirlemek için, açıkça vektörler



-
(37)
ve
-
(38)
-
(39)
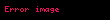


Dikkate alınız ki bu aralıklar arasında alan vardır.
Hiperbolik bir yörünge için (28) ve (29)dan yola çıkarak
-
(40)
and therefore that
-
(41)
ve sonuç olarak


-
(42)
Bu ilişki gerçek anomali ve E parametresi arasında geçiş yapmak için uygundur. (burada E (34)’e zaman yönünden bağlıdır.) Aralık arasındaki alana dikkat ediniz.
ve aşağıdaki bağla açıklanabilir.
(27)’ye bakarak, P’nin elips bir yörünge için yörünge periyodu
-
(43)
Kuvvet alanına potansiyel enerjinin ilgisi (1)
(13), (14), (18) ve (19)’ kadar kinetik ve potansiyel enerjinin özeti
Elips yörünge için
-
(44)
(13), (16), (18) ve (19)’den sonra kinetik ve potansiyel enerjinin hiperbol yörünge için
Eylemsizlik koordinat sistemiyle ilişkisi
-
(44)
and from (13), (16), olan bir yörünge düzleminde pericentre’ye doğru (18) ve (19)’dan yapılan hız elementleri çıkarımı
-
(45)
Belirli bir başlangıç durumuna karşılık Kepler yörüngesinin belirlenmesi
Bu diferansiyel denklemi (1) için "başlangıç değeri problemi" dir, ki 6 boyutlu bir durum vektründe ilk denklemdir ve şöyle yazılır
-
(46)
-
(47)
Başlangıç değeri vektörünün herhangi bir değeri için, bu başlangıç değeri probleminin çözümüne uygun Kepler Yörüngesi aşağıdaki algoritmayla bulunur
Ortogonal birim vektörleri Ayrıştırılamadı (SVG (MathML, tarayıcı eklentisi aracılığıyla etkinleştirilebilir): Geçersiz yanıt ("Math extension cannot connect to Restbase.") sunucu "http://localhost:6011/tr.wikipedia.org/v1/":): {\displaystyle (\hat{r}\ ,\ \hat{t})} tanımalamak gerekirse
-
(50)
-
(51)
ve 

(13), (14), (18) ve (19)’dan sonra sırasını takip eder.
|
| (52) |


-
(53)
-
(54)
aşağıdakinin olduğu yerde
|
| (55) |
aynı r, 

Eğer bu Kepler yörüngesi aynı vektörlerine sahipse ve gerçek anomalisi (50) ve (51)de tanımladığı gibi ise, Kepler yörüngesinin 


Standart atalet sabit koordinat sistemi 

|
| (56) |
|
| (57) |
(53) ve (54)’ün 
örneğin
|
| (58) |
Diaresel bir yörüngeye uyan başlangıç durumunu 
Oskülatör kepler yörüngesi



Şimdi, eğer hareket denklemi aşağıdaki gibi ise
|
| (59) |
aşağıdakinin
bir fonksyion olup
aşağıdaki parametlere sahip olmaması gerekir.



T zamanında bu şekilde "hareket denkleminin" çözümü olarak aynı "durum vektör" olan (59) 'da hesaplanan Kepler yörüngesi bu durumda "oskülatör" olduğu söylenebilir. Bu konsept, şu durumda yararlıdır.
olmak üzere
küçük bir “bozucu güç”tür çünkü, bir örnekle açıklamak gerekirse diğer gök cisimlerinden sönük bir yer çekimi bu durumda örnek gösterilebilir. Oskülasyon halindeki Kepler yörüngesinin parametreleri, ancak o zaman yavaşça değişecek ve oskülasyon halindeki Kepler yörüngesi iyi bir tahminle oskülasyonun öncesinde ve sonrasında gerçek yörüngeye hatrı sayılır bir zaman diliminde girecektir. Bu konsept aynı zamanda bir roket uçuşu için de faydalı olabilir çünkü itme kapatıldığı zaman hangi Keppler yörüngesinde devam edebileceği belirlenmiş olur. “Daire olmaya yakın” bir yörünge konsepti için, dışmerkezli vektörü şeklinde tanımlamak yararlıdır. (53), (54) ve (56)’dan yola çıkarak:
-
(60)
Örneğin 

Ayrıca bakınız
Kaynakça
- El'Yasberg "Theory of flight of artificial earth satellites", Israel program for Scientific Translations (1967)
- Bate, Roger; Mueller, Donald; White, Jerry (1971). Fundamentals of Astrodynamics. Dover Publications, Inc., New York. ISBN .
- Copernicus, Nicolaus (1952), "Book I, Chapter 4, The Movement of the Celestial Bodies Is Regular, Circular, and Everlasting-Or Else Compounded of Circular Movements", On the Revolutions of the Heavenly Spheres, Great Books of the Western World, 16, Chicago: William Benton, ss. 497-838
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde veya sayfa baska bir dilden kotu bir bicimde tercume edilmistir Sayfa makine cevirisi veya dilde yetkinligi bulunmayan bir cevirmen tarafindan olusturulmus olabilir Lutfen ceviriyi gelistirmek icin yardim edin Temmuz 2022 Gok mekanigi olarak Kepler yorungesi veya Keplersel yorunge uc boyutlu uzayda iki boyutlu bir yorunge duzlemi olusturan bir elips parabol hiperbol benzeri bir yorunge cismininin hareketini aciklar Kepler yorungesi ayni zamanda duz bir cizgi de cizebilir Kepler yorungesi yalnizca nokta iki cismin nokta benzeri yercekimsel cekimlerini dikkate alir atmosfer suruklemesi gunes radyasyonu baskisi dairesel olmayan cisim merkezi ve bunun gibi bir takim seylerin diger cisimlerle girdigi cekim iliskileri nedeniyle ihmal eder Boylece Kepler problemi olarak bilinen iki cisim probleminin ozel durumlara bir cozum olarak atfedilir Klasik mekanigin bir teorisi olarak ayni zamanda genel gorelilik etkilerini dikkate almaz Kepler yorungeleri cesitli sekillerde alti yorunge unsurlari icine parametrize edilebilir Kepler Orbitand eksentriklerini cesitli bicimlerde gosteren diyagram Mavi bir hiperbolik yorunge e gt 1 dir Yesil bir parabolik yorunge e 1 dir Kirmizi eliptik yorunge 0 lt e lt 1 Gri bir dairesel yorunge e 0 dir e 0 Cogu uygulamalarda tum sistemin kutle merkezi olarak kabul edilen buyuk bir merkezi cisim ve kutle merkezi vardir Ayristirma yapilinca iki objenin benzer kutleleri ikisinin ortak kutle merkezinin Kepler yorungesi ya da barisentileri olarak aciklanabilir GirisEski caglardan itibaren 16 ve 17 yuzyillara kadar gezegenlerin hareketlerinin Antik Yunan filozoflari Aristo ve Batlamyus tarafindan ogretildigi gibi mukemmel dairesel jeosentrik yollari takip ettigine inanilirdi Gezegenlerin hareketler degisimleri epidaire ust uste kucuk dairesel yollar seklinde aciklanmistir Gezegenlerin olcumleri giderek daha kesin olmaya basladiginda bu teoriye revizyonlar onerilmistir Hala gezegenlerin gunes merkezli mukemmel dairesel yorungede gittigine inanilmasina ragmen 1543 yilinda Nicolaus Copernicus gunes sisteminin bir gunes merkezli modelini yayinladi Yasalarin gelistirilmesi1601 yilinda Johannes Kepler Tycho Brahe tarafindan yapilan gezegenlerin kapsamli ve titiz gozlemlerini elde etti Kepler sonraki bes yili Mars gezegeninin gozlemlerini cesitli egrilere uydurmaya calisarak gecirecekti 1609 yilinda Kepler gezegensel hareketin uc yasasindan ilk ikisini yayinladi Birinci yasa soyledir Gunes sistemindeki butun gezegenler odaklarinin birinde Gunes olan elips seklindeki bir yorungede hareket ederler Daha genel anlatimla Kepler hareketini yapan bir nesnenin yolu elips oldugu kadar parabol veya hiperbol de olabilir Bu bir grup sekil konik kesitler olarak bilinir Matematiksel olarak merkezi bir cisim ile yorungedeki bir cisim arasindaki mesafe su sekilde ifade edilebilir r 8 a 1 e2 1 ecos 8 displaystyle r theta frac a 1 e 2 1 e cos theta r displaystyle r mesafedir a displaystyle a yorungenin boyutunu tanimlayan yari buyuk eksendir e displaystyle e yorungenin seklini tanimlayan dis merkezliktir 8 displaystyle theta yorungedeki nesnenin mevcut konumu ile yorungedeki merkez cisme en yakin oldugu enberi noktasi olarak adlandirilan konum arasindaki aci olan Alternatif olarak denklem su sekilde ifade edilebilir r 8 p1 ecos 8 displaystyle r theta frac p 1 e cos theta Burada p displaystyle p egrinin yari ozkirisi olarak adlandirilir Denklemin bu formu ozellikle yari buyuk ekseni sonsuz olan parabolik yorungelerle ugrasirken kullanislidir Bu yasalari gozlemleriyle gelistiren Kepler hicbir zaman bu hareketleri aciklayacak bir teori gelistirememistir Isaac Newton Isaac Newton 1665 ve 1666 yillari arasinda hareket kutlecekim ve diferansiyel hesap ile ilgili cesitli kavramlar gelistirdi Bununla birlikte bu kavramlar 1687 yilinda hareket yasalarini ve evrensel kutlecekim yasasini ana hatlariyla belirttigi Principia ya kadar yayinlanmadi Uc hareket yasasindan ikincisi soyle der Bir cismin ivmesi cisme etki eden net kuvvetle paralel ve dogru orantilidir Net kuvvet yonundedir ve cismin kutlesi ile ters orantilidir F ma md2rdt2 displaystyle mathbf F m mathbf a m frac d 2 mathbf r dt 2 F displaystyle mathbf F kuvvet vektorudur m displaystyle m kuvvetin etki ettigi cismin kutlesidir a displaystyle mathbf a ivme vektorudur r displaystyle mathbf r konum vektorunun ikinci zaman turevidir Kurallara bakilirsa denklemin bu sekli yalnizca asagida yapilan basitlestirici varsayimlara dayali olarak dogru olan sabit kutleli bir nesne icin gecerlidir Newton un evrensel kutlecekim yasasinin mekanizmalari Bir nokta kutle olan m1 diger bir nokta kutle olan m2 yi iki kutlenin carpimi ile orantili ve aralarindaki r uzakliginin karesi ile ters orantili olan bir F2 kuvveti ile ceker Kutleler veya mesafeden bagimsiz olarak F1 ve F2 nin buyuklukleri her zaman esit olacaktir G kutle cekimi sabitidir Newton un kutlecekim yasasi soyle der Her nokta kutle her iki noktayi kesen dogru boyunca isaret edilen bir kuvvetle diger nokta kutleleri ceker Kuvvet iki kutlenin carpimi ile orantili ve nokta kutleler arasindaki uzakligin karesi ile ters orantilidir F Gm1m2r2 displaystyle F G frac m 1 m 2 r 2 F displaystyle F iki nokta kutlesi arasindaki kutlecekim kuvvetinin buyuklugudur G displaystyle G kutle cekimi sabitidir m1 displaystyle m 1 birinci nokta kutlesinin kutlesidir m2 displaystyle m 2 ikinci nokta kutlesinin kutlesidir r displaystyle r iki nokta kutlesi arasindaki mesafedir Newton hareket yasalari ve evrensel kutlecekim yasasindan astronomide yorunge hareketine ozgu Kepler yasalarini turetebildi Kepler yasalari gozlem verileriyle iyi bir sekilde desteklendiginden bu tutarlilik Newton un genellestirilmis teorisinin ve birlesik goksel ve siradan mekanigin gecerliligine guclu bir destek sagladi Bu hareket yasalari 20 yuzyilin baslarinda Albert Einstein ozel ve genel gorelilik kavramlarini ortaya koyana kadar modern gok mekaniginin temelini olusturdu Cogu kullanimda Kepler hareketi gezegenlerin ve uydularin hareketlerini nispeten yuksek dogruluk derecelerine yaklastirir ve astronomi ve astrodinamikte yaygin olarak kullanilir Sadelestirilmis iki cisim problemi Iki cisimli bir sistemde bir cismin hareketini cozmek icin iki sadelestirici varsayim yapilabilir Cisimler kuresel olarak simetriktir ve nokta kutleler olarak ele alinabilir Cisimlere karsilikli kutlecekimi disinda etki eden ic ve dis kuvvetler yoktur Buyuk gok cisimlerinin sekilleri kurelere yakindir Simetri ile bir kutle noktasini homojen bir kureye dogru ceken net kutlecekim kuvveti merkeze dogru yonlenmelidir Isaac Newton tarafindan da kanitlanmis olan kurenin yogunlugu derinlige gore degisse bile cogu gok cisimleri icin oldugu gibi bu kuvvetin buyuklugunun kutlenin tamami kurenin ortasinda toplanmis gibi ayni oldugunu belirtir Bundan hemen sonra iki homojen kure arasindaki cekim her ikisinin de kutlesi merkezinde yogunlasmis gibidir Asteroitler veya uzay araclari gibi daha kucuk nesneler genellikle bir kureden guclu bir sekilde ayrilan bir sekle sahiptir Ancak bu duzensizlikler tarafindan uretilen kutlecekim kuvvetleri merkezi cismin kutlecekimi ile karsilastirildiginda genellikle onemsizdir Duzensiz bir sekil ile mukemmel bir kure arasindaki fark da mesafelerle azalir ve yorunge mesafelerinin cogu yorungedeki kucuk bir cismin capiyla karsilastirildiginda cok buyuktur Bu nedenle bazi durumlar icin sekil duzensizligi kesinlik uzerinde onemli bir etki olmaksizin ihmal edilebilir Bu etki ozellikle alcak yorungelerde bulunan yapay Dunya uydulari icin oldukca belirgindir Gezegenler degisen hizlarda donerler ve bu merkezkac kuvveti nedeniyle hafif basik bir sekil alabilirler Boyle yassi bir sekille kutle cekimi homojen bir kureninkinden bir miktar sapacaktir Daha buyuk mesafelerde bu yassiligin etkisi ihmal edilebilir hale gelir Gunes Sistemindeki gezegensel hareketler nokta kutleler olarak ele alinirsa yeterli hassasiyetle hesaplanabilirler Kutleleri m1 displaystyle m 1 ve m2 displaystyle m 2 olan iki nokta kutle nesnesi ve bazi eylemsiz referans cercevesine goreceli konum vektorleri r1 displaystyle mathbf r 1 ve r2 displaystyle mathbf r 2 kutlecekim kuvvetlerine maruz kalir m1r 1 Gm1m2r2r displaystyle m 1 ddot mathbf r 1 frac Gm 1 m 2 r 2 mathbf hat r m2r 2 Gm1m2r2r displaystyle m 2 ddot mathbf r 2 frac Gm 1 m 2 r 2 mathbf hat r burada r displaystyle mathbf r kutle 1 in kutle 2 ye gore goreceli konum vektorudur ve su sekilde ifade edilir r r1 r2 displaystyle mathbf r mathbf r 1 mathbf r 2 r displaystyle mathbf hat r o yondeki birim vektordur ve r displaystyle r bu vektorun uzunlugudur Kendi kutlelerine bolmek ve ikinci denklemi birinciden cikarmak birinci cismin ikinciye gore ivmesi icin hareket denklemini verir r ar2r displaystyle ddot mathbf r frac alpha r 2 mathbf hat r 1 a displaystyle alpha yercekimi parametresidir ve esittir a G m1 m2 displaystyle alpha G m 1 m 2 Bircok uygulamada ucuncu bir sadelestirici varsayim yapilabilir Bu varsayim sadelestirilmis iki cisim problemini cozmek icin gerekli degildir ancak ozellikle Dunya yorungesindeki uydular ve Gunes in yorungesindeki gezegenlerle ilgili hesaplamalari basitlestirir Jupiter in kutlesi bile Gunes inkinden 1047 kat daha azdir bu da a degerinde 0 096 lik bir hata olusturur Dikkate deger istisnalar arasinda Dunya Ay sistemi kutle orani 81 3 Pluton Charon sistemi kutle orani 8 9 ve ikili yildiz sistemleri sayilabilir Bu varsayimlar altinda iki cisim problemi icin diferansiyel denklem matematiksel olarak tamamen cozulebilir ve Kepler in gezegensel hareket yasalarini takip ederek sonucta olusan yorungeye Kepler yorungesi denir Tum gezegenlerin yorungeleri yuksek dogrulukta Gunes etrafindaki Kepler yorungeleridir Kucuk sapmalar gezegenler arasindaki cok daha zayif kutlecekim etkilerinden ve Merkur durumunda genel gorelilikten kaynaklanmaktadir Dunya etrafindaki yapay uydularin yorungeleri makul bir tahminle Gunes Ay ve Dunya nin yassiligindan dolayi kucuk duzensizliklere sahip Kepler yorungeleridir Hareket denkleminin butun kutlecekim ve kutlecekim olmayan kuvvetlerin gunes radyasyon basinci ve atmosfer direnci gibi hesaba katilmasiyla sayisal olarak entegre edilmesi gereken yuksek dogruluktaki kullanimlarda Kepler yorunge kavramlari cok onemlidir ve yogun olarak kullanilir Kepler yorunge ogeleri Kepler yorunge ogeleri Kepler yorungesinin alti parametre ile tanimlanabilirliginden soz etmek gerekir Uc boyutlu uzayda hareket eden bir nesnenin hareket bir konum vektoru ve bir hiz vektoru ile karakterize edilir Her vektorun uc bileseni vardir bu yuzden uzayda bir yorunge tanimlamak icin gerekli degerlerin toplam sayisi altidir Bir yorunge Kepler Elementleri olarak bilinen ve pozisyon ve hizina bagli olarak olculebilen alti elementten olusur ki bunlarin ucu daha once gosterilmistir Bu alti uygun elementten bes tanesi yorunge icin degismezdir iki surekli degisen vektore bir tezat niteliginde olmak uzere Kendi yorungesinde icindeki bir nesnenin gelecekteki konumu tahmin edilebilir ve yeni konum ve hiz kolayca yorunge elemanlari ile elde edilebilir Bunlardan ikisi eksenin boyutunu ve seklin belirler Yarimajor eksen a displaystyle a eksantriklik e displaystyle e Uc tanesi yorunge alaninin oryantasyonunu belirler egim i displaystyle i yorunge duzlemi ile referans duzlemi arasindaki aciyi tanimlar Yukselen nodun uzunlugu W displaystyle Omega Referans yonu ve referans duzlemi uzerinde yorungeye yukari kesisme yukselen nod arasindaki aciyi tanimlar Periapsis arguman w displaystyle omega artan nod ve periapsis arasindaki aciyi belirler Ve son olarak Gercek anomali n displaystyle nu periapsis olculen yorunge boyunca yorungedeki cismin konumunu tanimlar Cesitli baska degerlerin yerine gercek bir anomali kullanilabilir bunlardan en sik kullanilanlari mean anomoli olan M displaystyle M ve periapsisden yana gecen sure olan T displaystyle T dir i displaystyle i W displaystyle Omega ve w displaystyle omega sadece yorunge duzlemi icinde nesnenin hareketini tartisirken referans cercevesinde yorunge yonunu tanimlayan acisal olcumlerdir ve kesin olarak gerekli degildir Burada tamamlanmislik adina belitilmislerdir ancak asagidaki ispatlar icin gerekli degillerdir Yukaridaki diferansiyel denklemin 1 matematiksel cozumu Herhangi bir merkez kuvveti altinda yani r bir kuvvet paraleli ve hareket icin belirli bagil acisal momentumu H r r displaystyle mathbf H mathbf r times dot mathbf r sabit kalir H ddt r r r r r r 0 0 0 displaystyle dot mathbf H frac d dt left mathbf r times dot mathbf r right dot mathbf r times dot mathbf r mathbf r times ddot mathbf r mathbf 0 mathbf 0 mathbf 0 Pozisyonun capraz urunu vektor ve onun hizi oldugu icin sabit kaldigindan ayni duzelmde bulunmak zorundadirlar H displaystyle mathbf H ye ortogonal Bu vektor fonksiyonun bir duzlem egrisi oldugu anlamina gelir Denklemin kokeni etrafinda simetri vardir cunku kutupsal koordinatlarda cozmek kolaydir Bununla birlikte bu denklem dikkat etmek onemlidir 1 dogrusal ivmeye refere eder r displaystyle left ddot mathbf r right acisalin karsiti olarak 8 displaystyle left ddot theta right yahut radyal r displaystyle left ddot r right ivmelenme Bu nedenle denklemi degistiren kisinin dikkatli olmasi gerekir Simdi kartezyen koordinat sistemine x y displaystyle hat mathbf x hat mathbf y ve kutupsal birim vektorlere r 8 displaystyle hat mathbf r hat boldsymbol theta duzlemi octoganelinde bakalim H displaystyle mathbf H r cos 8 x sin 8 y displaystyle hat mathbf r cos theta hat mathbf x sin theta hat mathbf y 8 sin 8 x cos 8 y displaystyle hat boldsymbol theta sin theta hat mathbf x cos theta hat mathbf y Simdi vektor r displaystyle mathbf r fonksiyonunu yeniden yazabiliriz ve diferansiyali soyledir as r r cos 8x sin 8y rr displaystyle mathbf r r cos theta hat mathbf x sin theta hat mathbf y r hat mathbf r r r r r8 8 displaystyle dot mathbf r dot r hat mathbf r r dot theta hat boldsymbol theta r r r8 2 r r8 2r 8 8 displaystyle ddot mathbf r ddot r r dot theta 2 hat mathbf r r ddot theta 2 dot r dot theta hat boldsymbol theta Vektor calculusunu inceleyiz Bunlari yerine yazarsak sunu buluruz 1 r r8 2 r r8 2r 8 8 mr2 r 0 8 displaystyle ddot r r dot theta 2 hat mathbf r r ddot theta 2 dot r dot theta hat boldsymbol theta left frac mu r 2 right hat mathbf r 0 hat boldsymbol theta Bu siradan olmayan polar diferansiyel denklem verir r r8 2 mr2 displaystyle ddot r r dot theta 2 frac mu r 2 2 Bu denklemi cozmek icin oncelikle her zaman diferansiyel lineerini ortadan kaldirmak gerekir Suna ulasiriz H r r rcos 8 rsin 8 0 r cos 8 rsin 8 8 r sin 8 rcos 8 8 0 0 0 r28 r28 displaystyle H mathbf r times dot mathbf r r cos theta r sin theta 0 times dot r cos theta r sin theta dot theta dot r sin theta r cos theta dot theta 0 0 0 r 2 dot theta r 2 dot theta 8 Hr2 displaystyle dot theta frac H r 2 3 3 un zaman diferansiyalinii aldigimiz zaman suna ulasiriz 8 2 H r r3 displaystyle ddot theta frac 2 cdot H cdot dot r r 3 4 3 ve 4 denklemleri in diferansiyellerini elememize izin verir In order to eliminate the time derivatives of 8 displaystyle theta in zaman diferansiyellerini ellimine etmek icin uygun kisaltmalari bulmak bunun icin de zincir kurali kullanmamiz gerekir r drd8 8 displaystyle dot r frac dr d theta cdot dot theta 5 r d2rd82 8 2 drd8 8 displaystyle ddot r frac d 2 r d theta 2 cdot dot theta 2 frac dr d theta cdot ddot theta 6 r r8 2 mr2 displaystyle ddot r r dot theta 2 frac mu r 2 d2rd82 8 2 drd8 8 r8 2 mr2 displaystyle frac d 2 r d theta 2 cdot dot theta 2 frac dr d theta cdot ddot theta r dot theta 2 frac mu r 2 d2rd82 Hr2 2 drd8 2 H r r3 r Hr2 2 mr2 displaystyle frac d 2 r d theta 2 cdot left frac H r 2 right 2 frac dr d theta cdot left frac 2 cdot H cdot dot r r 3 right r left frac H r 2 right 2 frac mu r 2 H2r4 d2rd82 2 drd8 2r r mr2 displaystyle frac H 2 r 4 cdot left frac d 2 r d theta 2 2 cdot frac left frac dr d theta right 2 r r right frac mu r 2 7 Diferansiyel denklem 7 degisken degisimi ile analitik cozulebilir r 1s displaystyle r frac 1 s 8 Bu verilenleri kullanarak in 2 deki tum zaman diferansiyelleri yoksayilabilir ve bizi r8 displaystyle r theta r r8 2 mr2 displaystyle ddot r r dot theta 2 frac mu r 2 d2rd82 2s3 dsd8 2 1s2 d2sd82 displaystyle frac d 2 r d theta 2 frac 2 s 3 cdot left frac ds d theta right 2 frac 1 s 2 cdot frac d 2 s d theta 2 10 10 ve 9 da belirtilenleri d2rd82 displaystyle frac d 2 r d theta 2 ve drd8 displaystyle frac dr d theta icin kullanarak H2 d2sd82 s m displaystyle H 2 cdot left frac d 2 s d theta 2 s right mu 11 genel bir sonuca ulasilir s mH2 1 e cos 8 80 displaystyle s frac mu H 2 cdot left 1 e cdot cos theta theta 0 right 12 e ve 80 displaystyle theta 0 un baslangictaki s ve dsd8 displaystyle frac ds d theta n baslangic degerlerinin integral sabitleri olursa integralinin sabitini kullanmak yerine birim vektorleri kullanima alinir ve secilen yorunge alanindaki koordinat sistemini belirler boylece sifir degerini alir ve e is pozitiftir Bu su anlama gelir in maksimum oldugu yerde sifirdir ve boylece minimumdur p parametresini H2m displaystyle frac H 2 mu olarak tanimlarsak su ortaya cikar Alternatif turevi Bu denklemi polar diferansiyel denklemini kullanmadan cozmenin bir diger yolu soyledir u displaystyle mathbf u yu bir birim vektor olarak tanimlayin ornegin r ru displaystyle mathbf r r mathbf u and r mr2u displaystyle ddot mathbf r frac mu r 2 mathbf u gibi Burdan yola cikarak H r r ru ddt ru ru ru r u r2 u u rr u u r2u u displaystyle mathbf H mathbf r times dot mathbf r r mathbf u times frac d dt r mathbf u r mathbf u times r dot mathbf u dot r mathbf u r 2 mathbf u times dot mathbf u r dot r mathbf u times mathbf u r 2 mathbf u times dot mathbf u Simdi sunu degerlendiriniz r H mr2u r2u u mu u u m u u u u u u displaystyle ddot mathbf r times mathbf H frac mu r 2 mathbf u times r 2 mathbf u times dot mathbf u mu mathbf u times mathbf u times dot mathbf u mu mathbf u cdot dot mathbf u mathbf u mathbf u cdot mathbf u dot mathbf u Uclu vektor urunu Sunu dikkate aliniz u u u 2 1 displaystyle mathbf u cdot mathbf u mathbf u 2 1 u u 12 u u u u 12ddt u u 0 displaystyle mathbf u cdot dot mathbf u frac 1 2 mathbf u cdot dot mathbf u dot mathbf u cdot mathbf u frac 1 2 frac d dt mathbf u cdot mathbf u 0 Bu verileri bir onceki denkleme yerlestirdigimizde r H mu displaystyle ddot mathbf r times mathbf H mu dot mathbf u Iki tarafin da integralini alirsak r H mu c displaystyle dot mathbf r times mathbf H mu mathbf u mathbf c Burada csabit vektordur Bunur ile birlestirmek ortaya ilginc bir sonuc cikarir r r H r mu c mr u r c mr u u rccos 8 r m ccos 8 displaystyle mathbf r cdot dot mathbf r times mathbf H mathbf r cdot mu mathbf u mathbf c mu mathbf r cdot mathbf u mathbf r cdot mathbf c mu r mathbf u cdot mathbf u rc cos theta r mu c cos theta Burada 8 displaystyle theta r displaystyle bar r ve c displaystyle bar c arasindaki acidir r ye gore cozersek r r r H m ccos 8 r r Hm ccos 8 H 2m ccos 8 displaystyle r frac mathbf r cdot dot mathbf r times mathbf H mu c cos theta frac mathbf r times dot mathbf r cdot mathbf H mu c cos theta frac mathbf H 2 mu c cos theta Dikkat ediniz ki r 8 displaystyle r theta vektor fonksiyonunun polar koordinatlaridir Verilenleri yerine koyarsak ve su denkleme ulasiriz r p1 e cos 8 displaystyle r frac p 1 e cdot cos theta 13 Bu fokal noktada merkezi olan bir konik bolmenin polar koordinatlarinin denklemidir 8 displaystyle theta Argumanina gercek anomali denir Yorunge denkleminin ozellikleri e 0 displaystyle e 0 ise bu capi p olan bir dairedir 0 lt e lt 1 displaystyle 0 lt e lt 1 ise bu asagidakine sahip bir elipstir a p1 e2 displaystyle a frac p 1 e 2 14 b p1 e2 a 1 e2 displaystyle b frac p sqrt 1 e 2 a cdot sqrt 1 e 2 15 e 1 displaystyle e 1 ise fokal uzunlugu p2 displaystyle frac p 2 olan bir dairedir e gt 1 displaystyle e gt 1 ise bir asagidakine sahip bir hiperboldur a pe2 1 displaystyle a frac p e 2 1 16 b pe2 1 a e2 1 displaystyle b frac p sqrt e 2 1 a cdot sqrt e 2 1 17 Sonraki gorsel bir elipsi kirmizi bir paraboolu yesil ve bir hiperbolu mavi gosterir Dis merkezi 0 7 olan bir elips Kepler yorungesi Parabol Kepler yorungesi ve dis merkezi 1 3 olan bir Kepler yorungesi Fokal noktaya olan uzaklik denklemle de gosterildigi gibi polar acinin yatay cizgiye yakin acisinin bir fonksiyonudur 13 Yatay cizgi uzerinde nokta odak noktasindan saga dogru cikiyorsa nokta 8 0 displaystyle theta 0 odak noktasina olan minimum uzaklik p1 e displaystyle frac p 1 e degerini alir pericentre Elips icin de odak uzakligi maksimum degerini aldigi bir apocentre vardirp1 e displaystyle frac p 1 e Hiperbol icin 8 displaystyle theta nin araligi cos 1 1e lt 8 lt cos 1 1e displaystyle left cos 1 left frac 1 e right lt theta lt cos 1 left frac 1 e right right Bir parabol icin aralik p lt 8 lt p displaystyle left pi lt theta lt pi right Diferansiyelin zinci kuralini kullanarak 5 2 denklemi ve p nin tanimi H2m displaystyle frac H 2 mu olmak uzere radyal hiz elemani sudur Vr r Hp e sin 8 mp e sin 8 displaystyle V r dot r frac H p cdot e cdot sin theta sqrt frac mu p cdot e cdot sin theta 18 ve tegetsel bilesen olan hiz bileseni Vr displaystyle V r ye dik Vt r 8 Hr mp 1 e cos 8 displaystyle V t r cdot dot theta frac H r sqrt frac mu p cdot 1 e cdot cos theta 19 Polar argumani 8 displaystyle theta ve zaman t arasindaki baglanti elips ve hiperbolik yorungeler icin kucuk degisiklikler gosterebilir Elips seklindeki bir yorunge icin dis merkezli anomali olan E ye geceriz ve burdan x a cos E e displaystyle x a cdot cos E e 20 y b sin E displaystyle y b cdot sin E 21 ve sonuc olarak x a sin E E displaystyle dot x a cdot sin E cdot dot E 22 y b cos E E displaystyle dot y b cdot cos E cdot dot E 23 acisal momentum H olmak uzere H x y y x a b 1 e cos E E displaystyle H x cdot dot y y cdot dot x a cdot b cdot 1 e cdot cos E cdot dot E 24 Zamana gore entegrasyon olan t ile su sonuca ulasilir H t a b E e sin E displaystyle H cdot t a cdot b cdot E e cdot sin E 25 zaman varsayimini yaparak integral sabiti 0 olur p nin tanimi geregi H m p displaystyle H sqrt mu cdot p 26 su sekilde yazilabiir t a am E e sin E displaystyle t a cdot sqrt frac a mu E e cdot sin E 27 Hiperbolik bir yorunge icin parametre yaratmak icin hiperbolik fonksiyon kullanilir x a e cosh E displaystyle x a cdot e cosh E 28 y b sinh E displaystyle y b cdot sinh E 29 bu durumda suna ulasilir x a sinh E E displaystyle dot x a cdot sinh E cdot dot E 30 y b cosh E E displaystyle dot y b cdot cosh E cdot dot E 31 acisal momentum H olmak uzere H x y y x a b e cosh E 1 E displaystyle H x cdot dot y y cdot dot x a cdot b cdot e cdot cosh E 1 cdot dot E 32 Zamana gore entegrasyon olan t ile su sonuca ulasilir H t a b e sinh E E displaystyle H cdot t a cdot b cdot e cdot sinh E E 33 ornegin t a am e sinh E E displaystyle t a cdot sqrt frac a mu e cdot sinh E E 34 t nin hangi zamanda belirli bir gercek anomaliye 8 displaystyle theta ne ulastigini bulmak icin buna uyan parametre olan E nin 27 ile zamana olan bagini hesaplamasi elips icin 34 ile bagini ve hiperbolik yorunge icin Dikkat ediniz ki 27 ve 34 bu aralikta bir yer belirler lt t lt lt E lt displaystyle left infty lt t lt infty right longleftrightarrow left infty lt E lt infty right Bazi ilave formuller Ayrica bakiniz Merkez denklemi analitik acilimlar 20 ve 21 den edilinen elips yorunge icin r a 1 e cos E displaystyle r a cdot 1 e cdot cos E 35 ve buna gore cos 8 xr cos E e1 e cos E displaystyle cos theta frac x r frac cos E e 1 e cdot cos E 36 36 dan devam ettigimizde su sonuc cikar tan2 82 1 cos 81 cos 8 1 cos E e1 e cos E1 cos E e1 e cos E 1 e cos E cos E e1 e cos E cos E e 1 e1 e 1 cos E1 cos E 1 e1 e tan2 E2 displaystyle tan 2 frac theta 2 frac 1 cos theta 1 cos theta frac 1 frac cos E e 1 e cdot cos E 1 frac cos E e 1 e cdot cos E frac 1 e cdot cos E cos E e 1 e cdot cos E cos E e frac 1 e 1 e cdot frac 1 cos E 1 cos E frac 1 e 1 e cdot tan 2 frac E 2 Dis merkezli anomalinin geometrik yapisini belirlemek icin acikca vektorler cos E sin E displaystyle cos E sin E ve cos 8 sin 8 displaystyle cos theta sin theta nin x aksisiyle ayni yanda olmalari gerekir Buradan yola cikarak cos E2 sin E2 displaystyle left cos frac E 2 sin frac E 2 right ve cos 82 sin 82 displaystyle left cos frac theta 2 sin frac theta 2 right ayni ceyrek daireye sahiptir Burdan yola cikarak tan 82 1 e1 e tan E2 displaystyle tan frac theta 2 sqrt frac 1 e 1 e cdot tan frac E 2 37 ve 8 2 arg 1 e cos E2 1 e sin E2 n 2p displaystyle theta 2 cdot operatorname arg left sqrt 1 e cdot cos frac E 2 sqrt 1 e cdot sin frac E 2 right n cdot 2 pi 38 E 2 arg 1 e cos 82 1 e sin 82 n 2p displaystyle E 2 cdot operatorname arg left sqrt 1 e cdot cos frac theta 2 sqrt 1 e cdot sin frac theta 2 right n cdot 2 pi 39 x y displaystyle x y vektorunun polar argumanlarininve n arg x y displaystyle operatorname arg x y orneginde oldugu gibi secilmis olmasi gerekir arg x y displaystyle operatorname arg x y nin sayisal hesaplamasi icin standart ATAN2 y x fonksiyonunun ya ikili DATAN2 y x FORTRAN gibi programlama dillerinde kullanilmasi mumkundur Dikkate aliniz ki bu araliklar arasinda alan vardir lt 8 lt lt E lt displaystyle left infty lt theta lt infty right longleftrightarrow left infty lt E lt infty right Hiperbolik bir yorunge icin 28 ve 29 dan yola cikarak r a e cosh E 1 displaystyle r a cdot e cdot cosh E 1 40 and therefore that cos 8 xr e cosh Ee cosh E 1 displaystyle cos theta frac x r frac e cosh E e cdot cosh E 1 41 ve sonuc olarak tan2 82 1 cos 81 cos 8 1 e cosh Ee cosh E 11 e cosh Ee cosh E 1 e cosh E e cosh Ee cosh E e cosh E e 1e 1 cosh E 1cosh E 1 e 1e 1 tanh2 E2 displaystyle tan 2 frac theta 2 frac 1 cos theta 1 cos theta frac 1 frac e cosh E e cdot cosh E 1 1 frac e cosh E e cdot cosh E 1 frac e cdot cosh E e cosh E e cdot cosh E e cosh E frac e 1 e 1 cdot frac cosh E 1 cosh E 1 frac e 1 e 1 cdot tanh 2 frac E 2 tan 82 displaystyle tan frac theta 2 ve tanh E2 displaystyle tanh frac E 2 asagidaki ifadeyi saglayan ayni isarete sahiptir tan 82 e 1e 1 tanh E2 displaystyle tan frac theta 2 sqrt frac e 1 e 1 cdot tanh frac E 2 42 Bu iliski gercek anomali ve E parametresi arasinda gecis yapmak icin uygundur burada E 34 e zaman yonunden baglidir Aralik arasindaki alana dikkat ediniz cos 1 1e lt 8 lt cos 1 1e lt E lt displaystyle left cos 1 left frac 1 e right lt theta lt cos 1 left frac 1 e right right longleftrightarrow left infty lt E lt infty right ve asagidaki bagla aciklanabilir tanh 1 x 12ln 1 x1 x displaystyle tanh 1 x frac 1 2 ln left frac 1 x 1 x right 27 ye bakarak P nin elips bir yorunge icin yorunge periyodu P 2p a am displaystyle P 2 pi cdot a cdot sqrt frac a mu 43 Kuvvet alanina potansiyel enerjinin ilgisi 1 mr displaystyle frac mu r 13 14 18 ve 19 kadar kinetik ve potansiyel enerjinin ozeti Vr2 Vt22 mr displaystyle frac V r 2 V t 2 2 frac mu r Elips yorunge icin m2 a displaystyle frac mu 2 cdot a 44 13 16 18 ve 19 den sonra kinetik ve potansiyel enerjinin hiperbol yorunge icin Vr2 Vt22 mr displaystyle frac V r 2 V t 2 2 frac mu r Eylemsizlik koordinat sistemiyle iliskisi m2 a displaystyle frac mu 2 cdot a 44 and from 13 16 olan bir yorunge duzleminde pericentre ye dogru 18 ve 19 dan yapilan hiz elementleri cikarimi m2 a displaystyle frac mu 2 cdot a 45 Belirli bir baslangic durumuna karsilik Kepler yorungesinin belirlenmesi x y displaystyle hat x hat y Bu diferansiyel denklemi 1 icin baslangic degeri problemi dir ki 6 boyutlu bir durum vektrunde ilk denklemdir ve soyle yazilir Vx cos 8 Vr sin 8 Vt mp sin 8 displaystyle V x cos theta cdot V r sin theta cdot V t sqrt frac mu p cdot sin theta 46 Vy sin 8 Vr cos 8 Vt mp e cos 8 displaystyle V y sin theta cdot V r cos theta cdot V t sqrt frac mu p cdot e cos theta 47 Baslangic degeri vektorunun herhangi bir degeri icin bu baslangic degeri probleminin cozumune uygun Kepler Yorungesi asagidaki algoritmayla bulunur Ortogonal birim vektorleri Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle hat r hat t tanimalamak gerekirse r0 r r displaystyle bar r 0 r cdot hat r 50 v0 Vr r Vt t displaystyle bar v 0 V r cdot hat r V t cdot hat t 51 ve r gt 0 displaystyle r gt 0 and Vt gt 0 displaystyle V t gt 0 13 14 18 ve 19 dan sonra sirasini takip eder p r Vt 2m displaystyle p frac r cdot V t 2 mu 52 e 0 displaystyle e geq 0 and 8 displaystyle theta yi tanimlarken e cos 8 VtV0 1 displaystyle e cdot cos theta frac V t V 0 1 53 e sin 8 VrV0 displaystyle e cdot sin theta frac V r V 0 54 asagidakinin oldugu yerde V0 mp displaystyle V 0 sqrt frac mu p 55 ayni r Vr displaystyle V r and Vt displaystyle V t degerlerine sahip olan gercek anomaliye sahip bir Kepler yorungesi bulunur ve bu 50 ve 51 de gosterilmistir Eger bu Kepler yorungesi ayni vektorlerine sahipse ve gercek anomalisi 50 ve 51 de tanimladigi gibi ise Kepler yorungesinin r t displaystyle hat r hat t vektorleri istenen deger olan r0 v0 displaystyle bar r 0 bar v 0 yi gercek anomalisi 8 displaystyle theta olmak uzere alir Standart atalet sabit koordinat sistemi x y displaystyle hat x hat y yorungesel duzlemde x displaystyle hat x pericentre nin homojen kuresindin merkezinden gelecek sekilde konik alanin oryantasyonunu belirliyorsa elips parabol hiperbol bu iliskiyle hesaplanabilir x cos 8 r sin 8 t displaystyle hat x cos theta cdot hat r sin theta cdot hat t 56 y sin 8 r cos 8 t displaystyle hat y sin theta cdot hat r cos theta cdot hat t 57 53 ve 54 un Vr 0 displaystyle V r 0 oldugu durumda baglantili olduguna dikkat ediniz ve Vt V0 mp m r Vt 2m displaystyle V t V 0 sqrt frac mu p sqrt frac mu frac r cdot V t 2 mu ornegin Vt mr displaystyle V t sqrt frac mu r 58 Diaresel bir yorungeye uyan baslangic durumunu r0 v0 displaystyle bar r 0 bar v 0 gosterir Oskulator kepler yorungesi r v displaystyle bar r bar v gibi herhangi bir durum vektoru icin bu durumdaki Kepler yorungesi asagida tanilmlanan algoritma ile hesaplanabilir Ilk parametreler p e 8 displaystyle p e theta ile belirlenir ve x y displaystyle hat x hat y yorungesel duzelemde ortogonal birim vektorleri de 56 ve 57 arasindaki iliskiyi kullanarak bulunur Simdi eger hareket denklemi asagidaki gibi ise r F r r t displaystyle ddot bar r operatorname bar F bar r dot bar r t 59 asagidakinin F r r t displaystyle operatorname bar F bar r dot bar r t bir fonksyion olup m r r2 displaystyle mu cdot frac hat r r 2 asagidaki parametlere sahip olmamasi gerekir p e 8 x y displaystyle p e theta hat x hat y r r displaystyle bar r dot bar r tarafindan tanimlanmis zaman icinde degisecek olan durumlar Keppler Yorungesinin tersine yalnizca 8 displaystyle theta da degisecektir T zamaninda bu sekilde hareket denkleminin cozumu olarak ayni durum vektor olan 59 da hesaplanan Kepler yorungesi bu durumda oskulator oldugu soylenebilir Bu konsept su durumda yararlidir F r r t m r r2 f r r t displaystyle operatorname bar F bar r dot bar r t mu cdot frac hat r r 2 operatorname bar f bar r dot bar r t olmak uzere f r r t displaystyle operatorname bar f bar r dot bar r t kucuk bir bozucu guc tur cunku bir ornekle aciklamak gerekirse diger gok cisimlerinden sonuk bir yer cekimi bu durumda ornek gosterilebilir Oskulasyon halindeki Kepler yorungesinin parametreleri ancak o zaman yavasca degisecek ve oskulasyon halindeki Kepler yorungesi iyi bir tahminle oskulasyonun oncesinde ve sonrasinda gercek yorungeye hatri sayilir bir zaman diliminde girecektir Bu konsept ayni zamanda bir roket ucusu icin de faydali olabilir cunku itme kapatildigi zaman hangi Keppler yorungesinde devam edebilecegi belirlenmis olur Daire olmaya yakin bir yorunge konsepti icin dismerkezli vektoru seklinde tanimlamak yararlidir 53 54 ve 56 dan yola cikarak e Vt V0 r Vr t V0 displaystyle bar e frac V t V 0 cdot hat r V r cdot hat t V 0 60 Ornegin r v displaystyle bar r bar v durum vektorlerinin diferansiyel fonskyonlaridir e displaystyle bar e ayrica bu durum dairesel bir yorungeye karsilik geliyor ise de gecerlidir Ayrica bakinizIki cisim problemi Kutlecekimsel iki cisim problemi Kepler in gezegensel hareket yasalari Eliptik yorunge Hiperbolik yorunge Kacis yorungesiKaynakca Bate Mueller White s 177 181 Arsivlenmis kopya 16 Subat 2011 tarihinde kaynagindan Erisim tarihi 7 Kasim 2009 El Yasberg Theory of flight of artificial earth satellites Israel program for Scientific Translations 1967 Bate Roger Mueller Donald White Jerry 1971 Fundamentals of Astrodynamics Dover Publications Inc New York ISBN 0 486 60061 0 Copernicus Nicolaus 1952 Book I Chapter 4 The Movement of the Celestial Bodies Is Regular Circular and Everlasting Or Else Compounded of Circular Movements On the Revolutions of the Heavenly Spheres Great Books of the Western World 16 Chicago William Benton ss 497 838
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State