Matematikte, gerçel değerli bir fonksiyonun grafiğindeki herhangi iki ayrı nokta arasındaki doğru parçası, grafiğin üstünde veya üzerinde yer alıyorsa, bu fonksiyona dışbükey fonksiyon ya da konveks fonksiyon denir. Eşdeğer bir ifâdeyle, bir fonksiyonun (fonksiyonun grafiğinin üzerinde veya üstündeki noktaların kümesi) bir dışbükey küme ise fonksiyon dışbükeydir. Yine grafik üzerinden basitçe tarif etmek gerekirse, dışbükey bir fonksiyonun grafiği bir fincan ya da veya doğrusal bir fonksiyonda olduğu gibi düz bir çizgi şeklindedir. İçbükey bir fonksiyonun grafiği ise bir şapka gibi şekle sahiptir.


Tek değişkenli bir fonksiyon en az iki kez türevlenebilir ise, o zaman bu fonksiyonun dışbükeyliği ancak ve ancak ikinci türev (fonksiyonun tanım kümesinde) negatif değilse mümkündür. Tek değişkenli dışbükey fonksiyonların iyi bilinen örnekleri arasında gerçel olmak üzere biçimindeki doğrusal fonksiyonlar bulunur. negatif olmayan bir gerçel sayı olmak üzere biçimindeki ve biçimindeki üstel fonksiyonlar da örnek olarak alınabilir.
Dışbükey fonksiyonlar matematiğin birçok alanında önemli bir rol oynar. Özellikle, optimizasyon problemlerinde kullanışlı özellikleriyle önemlidirler. Örneğin, üzerindeki kesin dışbükey bir fonksiyonun birden fazla minimumu yoktur. Sonsuz boyutlu uzaylarda bile, uygun ek hipotezler altında, dışbükey fonksiyonlar bu tür özellikleri sağlamaya devam eder ve sonuç olarak, varyasyonlar hesabında en çok anlaşılmış fonksiyoneller dışbükey olanlardır. Olasılık teorisinde, bir rassal değişkenin beklenen değerine uygulanan bir dışbükey fonksiyon, her zaman rastgele değişkenin dışbükey fonksiyonunun beklenen değeri ile üstten sınırlıdır. Jensen eşitsizliği olarak bilinen bu sonuç, ve Hölder eşitsizliği gibi eşitsizlikleri çıkarmak için kullanılabilir.
Tanım




- Her
ve her
için
Eşitsizliğin sağındaki ifâde, - Her
ve
sağlayan bütün
için
Bu ikinci tanım şartının birinci tanım şartından temel farkı alınan doğru ile grafiğin kesişmesini istememesidir. Birinci koşulda
alırsak,
,
alırsak
olacaktır ki bu ifâdeler zâten doğrudur. Yine,
alırsak her zaman doğru olan ifâdeler ortaya çıkar. O yüzden, bu koşulları tanımdan çıkarmanın bir zararı yoktur.
 nin grafiğinde
nin grafiğinde  ve
ve  arasındaki doğruyu
arasındaki doğruyu  nin fonksiyonu olarak belirtir. Soldaki ifâdede ise,
nin fonksiyonu olarak belirtir. Soldaki ifâdede ise,  fonksiyonunun argümanı
fonksiyonunun argümanı  teki
teki  ve
ve  elemanları arasındaki doğruyu belirtir. Demek ki, bu koşul ile
elemanları arasındaki doğruyu belirtir. Demek ki, bu koşul ile  nin grafiğindeki iki noktayı bağlayan doğrunun ya grafiğin üzerinde ya da üstünde olması istenmektedir.
nin grafiğindeki iki noktayı bağlayan doğrunun ya grafiğin üzerinde ya da üstünde olması istenmektedir.Gerçel sayı doğrusu 












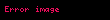
Kesin dışbükeylik
İkinci ifade, kesin dışbükeyliğin tanımını elde etmek için de değiştirilebilir ki burada eşitliğe de izin veren küçük eşittir gösterimi 





Kesin dışbükey fonksiyonların grafiğindeki iki farklı noktayı birleştiren doğru parçasının üç noktaları hariç geriye kalan bütün noktaları fonksiyonun grafiğinin üstünde kalır. Dışbükey olup da kesin dışbükey olmayan bir fonksiyona 
Bir fonksiyonun negatifi dışbükeyse (ya da kesin dışbükeyse), o zaman fonksiyona içbükey fonksiyon (ya da kesin içbükey fonksiyon) denir.
Dışbükeyimsi fonksiyon
Bir aralıkta (veya daha genel olarak vektör uzayındaki bir dışbükey kümede) tanımlı ve gerçel değerli bir 

eşitsizliğini tanım kümesindeki her 

Özellikler
Dışbükey fonksiyonların birçok özelliği, tek değişkenli fonksiyonlar için olduğu gibi çok değişkenli fonksiyonlar için de basitlikle ifâde edilebilir ve genelde de aynı formülasyona sahiptir. Bu yüzden, çok değişkenli fonksiyonlar için aşağıda verilen özelliklere de bakınız; bu özelliklerden bir değişkenli fonksiyonlar kısmında ayrıca bahsedilmemiştir.
Bir değişkenli fonksiyonlar
- Bir aralık üzerinde tanımlı ve gerçel değişkenli bir
fonksiyonunu ele alalım ve










- Bir
açık aralığı üzerinde tanımlı ve bir gerçel değişkenli bir fonksiyon dışbükeyse, o zaman bu aralık üzerinde süreklidir. Fonksiyonun aynı zamanda soldan ve sağdan türevleri de vardır ve türevler kesin azalmayandır. Ayrıca, sol türev soldan sürekli, sağ türev ise sağdan süreklidir. Sonuç olarak, fonksiyon en fazla sayılabilir bir küme haricinde türevlidir. Yine de, fonksiyonun türevli olmadığı noktalar yoğun olabilir. Eğer
kapalı aralıksa,
nin başlangıç ve bitiş noktalarında fonksiyonun sürekliliği olmayabilir.
- Türevlenebilir bir fonksiyonun bir aralıkta dışbükey olması için gerekli ve yeterli şart türevinin aynı aralıkta kesin azalmayan olmasıdır. Bir fonksiyon hem dışbükey hem de türevlenebilirse, o zaman, sürekli türevlenebilirdir; yâni, türevi de süreklidir.
- Bir gerçel değişkenli ve türevlenebilir bir fonksiyonun dışbükey olması için gerekli ve yeterli şart fonksiyonun grafiğinin bütün teğet doğrularının üstünde yer almasıdır; yâni, her
ve
için

- olmalıdır.
- Bir gerçel değişkenli ve iki kere türevlenebilir bir fonksiyonun dışbükey olması için gerekli ve yeterli şart ikinci türevinin negatif olmamasıdır.
- Dışbükey bir
fonksiyonu için
varsa, o zaman, bütün pozitif
ve
için
sağlanır.
- Kanıt:
dışbükey olduğu için, dışbükeylik tanımında
alarak bütün
için

- elde edilir.
olduğu için

- Böylece,
olur.
- Bir
aralığında tanımlı
fonksiyonu her
için

- özelliğini sağlıyorsa bu fonksiyon orta nokta dışbükeyliğini sağlıyordur. Bu özellik, dışbükeylikten daha zayıf bir özelliktir ve elbette bütün dışbükey fonksiyonlar bu özelliği sağlar. Tersi yönde ise Sierpiński'nin bir teoremi geçerlidir: Orta nokta dışbükeyliğini sağlayan bütün Lebesgue ölçülebilir fonksiyonlar aynı zamanda dışbükeydir. Daha da özelde, sürekli bir fonksiyon orta nokta dışbükeyliğini sağlıyorsa dışbükeydir.
Çok değişkenli fonksiyonlar
- Herbir değişkeninde ayrı ayrı dışbükey olan bir fonksiyon genel olarak dışbükey olmak zorunda değildir. Mesela,
fonksiyonu her bir değişkende (diğeri sabit tutularak) doğrusallıktan dolayı dışbükeydir ancak fonksiyonda tüm değişkenler aynı anda hesaba katıldığında dışbükey değildir.
- Genişletilmiş gerçel sayılar doğrusu
kümesinde değerler alan bir
fonksiyonunun dışbükeyliği için fonksiyonun
- biçiminde yazılabilen epigrafının dışbükey olması gerekli ve yeterlidir.
- Türevlenebilir bir
fonksiyonunun dışbükey olması için
eşitsizliğinin fonksiyonun tanım kümesindeki bütün
elemanları için sağlanması gerekli ve yeterlidir.
- İki kere türevlenebilen bir fonksiyonun bir dışbükey küme üzerinde dışbükey olması için Hesse matrisinin dışbükey kümenin içinde kesin pozitif matris olması gerekli ve yeterlidir.
- Bir
fonksiyonu dışbükeyse, o zaman
için
ve
dışbükey kümedir. Bu tür özellikleri sağlayan fonksiyonlara adı verilir ve her zaman dışbükey olmayabilirler.
- Bir dışbükey fonksiyonun yerel minimumu aynı zamanda mutlak minimumudur. Kesin dışbükey fonksiyonun en fazla bir tane mutlak minimumu olabilir.
- Jensen eşitsizliği bütün dışbükey fonksiyonlara uygulanabilir. Eğer
ile gösterilen bir rassal değişkenin değer kümesi, dışbükey bir
fonksiyonunun tanım kümesindeyse
olur. Burada,
beklenen değerdir. Gerçekten de, Jensen eşitsizliğinin hipotezini sağlayan fonksiyonlar dışbükey fonksiyonlardır.
eşitliğini bütün
için sağlayan birinci mertebeden iki değişkenli homojen fonksiyonlar, bir değişkeninde dışbükey ise diğer değişkende de dışbükeydir.
Dışbükeyliği koruyan işlemler
- Bir
fonksiyonun dışbükeyliği
fonksiyonunun içbükeyliğine denktir.
- Herhangi bir
gerçel sayısı için,
ancak ve ancak
dışbükeyse dışbükeydir.
ise ve
fonksiyonlarının hepsi dışbükeyse, o zaman
de dışbükeydir. Özellikle, iki dışbükey fonksiyonun toplamı yine dışbükeydir. Bu özellik, tanımlı oldukları sürece sonsuz toplamlara, integrallere ve beklenen değerlere de genişletilebilir.
- Dışbükey fonksiyonların bir noktadaki supremumu üzerinden tanımlanan fonksiyon da dışbükeydir. Diğer deyişle,
bir endis kümesi ise ve
kümeleri de bu fonksiyonların bu endis kümesine göre dışbükey bir ailesi ise, o zaman
fonksiyonu da dışbükeydir. Bu özelliğin özel bir durumu olarak,
- Dışbükey fonksiyonların maksimumu yine dışbükeydir. Yâni,
dışbükey fonksiyonlar ise, o zaman
fonksiyonu da dışbükeydir.
- :
fonksiyonu
değişkeninde dışbükey ise, o zaman
fonksiyonu da,
kümesi dışbükey olmasa bile, dışbükeydir.
- Dışbükey fonksiyonların maksimumu yine dışbükeydir. Yâni,
fonksiyonu
değişkeninde dışbükeyse, o zaman
fonksiyonu
değişkeninde
kümesi dışbükey ve
olduğu sürece dışbükeydir.
ve
fonksiyonları dışbükey fonksiyonlar ise ve
gerçel doğru üzerindeki bir kümede azalmıyor ise, o zaman
fonksiyonu da dışbükeydir. Örneğin,
dışbükeyse
de dışbükeydir çünkü
dışbükeydir ve kesin artandır. Benzer bir özellik ise şu durumda çıkar. Eğer
içbükeyse,
dışbükeyse ve
gerçel doğru üzerindeki bir kümede artmıyor ise, o zaman
de dışbükeydir.
- Dışbükeylik afin gönderimler altında değişmez bir özelliğe sahiptir. Diğer deyişle,
fonksiyonu bir
kümesi üzerinde dışbükey ise, o zaman,
kümesi de dışbükeydir. Burada,
ve
'nin tanım kümesi
alınmıştır.
dışbükeyse, tanım kümesi
olan
fonksiyonu da dışbükeydir.
bir vektör uzayı olsun.
fonksiyonun dışbükey olması ve
eşitsizliğini sağlaması ancak ve ancak
ve
özelliğini sağlayan her
için
- özelliği sağlanıyorsa mümkündür.
Güçlü dışbükey fonksiyonlar
Kesin dışbükeylik kavramını bir paramatre aracılığıyla genelleştiren güçlü dışbükeylik kavramı da mevcuttur. Sezgisel olarak, güçlü dışbükey bir fonksiyon, en az ikinci dereceden bir fonksiyon kadar hızlı büyüyen bir fonksiyondur. Güçlü dışbükey bir fonksiyon kesin dışbükeydir; ancak, bu ifâdenin tersi her zaman doğru değildir. Tek gerçel değişkene bağlı ve tanım kümesi reel sayı doğrusu olan bir 
nin dışbükeyliği ancak ve ancak her
için
ise mümkündür.
- Her
için
ise
kesin dışbükeydir; ancak, bu yeterli bir koşuldur ve gerekli değildir.
nin güçlü dışbükeyliği ancak ve ancak her
için
sağlayan pozitif gerçel bir
sayısı ile mümkündür.
Örneğin, 



Daha genel olarak, türevlenebilir bir 


Daha genel bir ifâdeyle, 

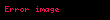

Yukarıda verilen şartlara eşdeğer bir şart da şöyle tanımlanabilir:
Bir fonksiyonun güçlü dışbükey olması için türevlenebilir olması gerekli değildir. Bir fonksiyonun 
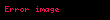






Bir 














Fonksiyonun iki kez sürekli olarak türevlenebilir olduğunu varsayarak 



Yine, bir 


Tanım kümesi tıkız bir 


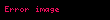

Güçlü dışbükey fonksiyonlar sınıfı daha küçük olduğu için bu tür fonksiyonlarla çalışılması dışbükey veya kesin dışbükey fonksiyonlara göre genellikle daha kolaydır. Kesin dışbükey fonksiyonlar gibi, güçlü dışbükey fonksiyonların da tıkız kümelerde biricik minimumu vardır.
Güçlü-dışbükey fonksiyonların özellikleri
Bir 

- Tüm gerçel
sayıları için
.
fonksiyonun
üzerinde bir mutlak ve biricik minimumu vardır.
Düzgün dışbükey fonksiyonlar



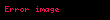






Örnekler
Bir değişkenli fonksiyonlar
fonksiyonu için
elde edilir. Bu yüzden, f dışbükey fonksiyondur. Aynı zamanda güçlü dışbükeydir (ki bu yüzden kesin dışbükeydir); güçlü dışbükeylik parametresi de 2 olur.
fonksiyonu için
olur. Bu yüzden, f dışbükey fonksiyondur. İkinci türevi bir noktada sıfır değeri alsa da, fonksiyon, yine de kesin dışbükeydir. Ancak, fonksiyon güçlü dışbükey değildir.
- Mutlak değer fonksiyonu dışbükeydir ki gösterimi üçgen eşitsizliğinden kolaylıkla elde edilir. Fonksiyonun grafiğinde
noktasınde görülen sivri uç türevin varlığına engeldir. Ayrıca, fonksiyon, kesin dışbükey değildir.
fonksiyonu
için dışbükeydir.
- Üstel fonksiyon
dışbükeydir.
olduğu için kesin dışbükeydir. Ancak, ikinci türev sıfıra keyfi derecede yakın olduğu için güçlü dışbükey değildir. Daha genel olarak,
fonksiyonu dışbükey olduğunda
fonksiyonu logaritmik dışbükey fonksiyon olur.
aralığında
olarak tanımlı fonksiyon
aralığında dışbükeydir.
açık aralığında süreklidir ama 0 and 1 noktalarında süreklilik yoktur.
fonksiyonunun ikinci türevi
olur. Bu yüzden,
olan noktalarda dışbükeydir,
olan noktalarda ise içbükeydir.
- Kesin artan ve dışbükey olmayan fonksiyonlara
ve
fonksiyonları örnek olarak verilebilir.
fonksiyonun ikinci türevi
olur.
iken ikinci türev pozitif olur; böylece,
aralığında
dışbükeydir.
aralığında ise fonksiyon içbükeydir.
fonksiyonu
olarak tanımlansın. O zaman, fonksiyon
ve
aralıklarında dışbükeydir. Ancak,
aralığında fonksiyonun dışbükeyliğinden bahsedilemez; çünkü,
nokasındaki tekillik bu dışbükeylik özelliğine izin vermez.
Çok değişkenli fonksiyonlar
- fonksiyonu dışbükeydir.
- olan
için
fonksiyonu dışbükeydir.
- Gerçel değerli her doğrusal dönüşüm dışbükeydir ama kesin dışbükey değildir. Gerçekten,
doğrusalsa, o zaman
olur. Aynı ifâde, dışbükeyliği içbükeylikle değiştirdiğimizde de doğrudur.
- Gerçel değerli her , yâni
biçimindeki fonksiyonlar, hem dışbükey hem de içbükeydir.
- , üçgen eşitsizliği ve özelliği sayesinde dışbükeydir.
- köşegen elemanlarının dışbükey fonksiyonudur.
Ayrıca bakınız
Kaynakça
- ^ "Lecture Notes 2" (PDF). www.stat.cmu.edu. 6 Mayıs 2021 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 3 Mart 2017.
- ^ "Concave Upward and Downward". 18 Aralık 2013 tarihinde kaynağından arşivlendi.
- ^ "dışbükeyimsi fonksiyon" Türkçe Bilim Terimleri Sözlüğü. Türkiye Bilimler Akademisi. Erişim tarihi: 06 Aralık 2024.
- ^ Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. ISBN . 9 Mayıs 2021 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 15 Ekim 2011.
- ^ Donoghue, William F. (1969). Distributions and Fourier Transforms. Academic Press. s. 12. ISBN . Erişim tarihi: 29 Ağustos 2012.
- ^ "If f is strictly convex in a convex set, show it has no more than 1 minimum". Math StackExchange. 21 Mart 2013. 28 Temmuz 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Mayıs 2016.
- ^ Altenberg, L., 2012. Resolvent positive linear operators exhibit the reduction phenomenon. Proceedings of the National Academy of Sciences, 109(10), pp.3705-3710.
- ^ "Strong convexity · Xingyu Zhou's blog". xingyuzhou.org. 12 Nisan 2024 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Eylül 2023.
- ^ Dimitri Bertsekas (2003). Convex Analysis and Optimization. Contributors: Angelia Nedic and Asuman E. Ozdaglar. Athena Scientific. s. 72. ISBN .
- ^ Philippe G. Ciarlet (1989). Introduction to numerical linear algebra and optimisation. Cambridge University Press. ISBN .
- ^ a b Yurii Nesterov (2004). Introductory Lectures on Convex Optimization: A Basic Course. Kluwer Academic Publishers. ss. 63-64. ISBN .
- ^ Nemirovsky and Ben-Tal (2023). "Optimization III: Convex Optimization" (PDF). 10 Aralık 2023 tarihinde kaynağından (PDF) arşivlendi.
- ^ a b C. Zalinescu (2002). Convex Analysis in General Vector Spaces. World Scientific. ISBN .
- ^ a b H. Bauschke and P. L. Combettes (2011). Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer. s. 144. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte gercel degerli bir fonksiyonun grafigindeki herhangi iki ayri nokta arasindaki dogru parcasi grafigin ustunde veya uzerinde yer aliyorsa bu fonksiyona disbukey fonksiyon ya da konveks fonksiyon denir Esdeger bir ifadeyle bir fonksiyonun fonksiyonun grafiginin uzerinde veya ustundeki noktalarin kumesi bir disbukey kume ise fonksiyon disbukeydir Yine grafik uzerinden basitce tarif etmek gerekirse disbukey bir fonksiyonun grafigi bir fincan displaystyle cup ya da veya dogrusal bir fonksiyonda oldugu gibi duz bir cizgi seklindedir Icbukey bir fonksiyonun grafigi ise bir sapka displaystyle cap gibi sekle sahiptir Bir aralik uzerinde disbukey fonksiyonun grafigiBir fonksiyon Siyahla ile gosterilmistir ancak ve ancak grafiginin ustunde kalan bolge disbukey kumeyse disbukeydir Tek degiskenli bir fonksiyon en az iki kez turevlenebilir ise o zaman bu fonksiyonun disbukeyligi ancak ve ancak ikinci turev fonksiyonun tanim kumesinde negatif degilse mumkundur Tek degiskenli disbukey fonksiyonlarin iyi bilinen ornekleri arasinda c displaystyle c gercel olmak uzere f x cx displaystyle f x cx bicimindeki dogrusal fonksiyonlar bulunur c displaystyle c negatif olmayan bir gercel sayi olmak uzere cx2 displaystyle cx 2 bicimindeki ve cex displaystyle ce x bicimindeki ustel fonksiyonlar da ornek olarak alinabilir Disbukey fonksiyonlar matematigin bircok alaninda onemli bir rol oynar Ozellikle optimizasyon problemlerinde kullanisli ozellikleriyle onemlidirler Ornegin uzerindeki kesin disbukey bir fonksiyonun birden fazla minimumu yoktur Sonsuz boyutlu uzaylarda bile uygun ek hipotezler altinda disbukey fonksiyonlar bu tur ozellikleri saglamaya devam eder ve sonuc olarak varyasyonlar hesabinda en cok anlasilmis fonksiyoneller disbukey olanlardir Olasilik teorisinde bir rassal degiskenin beklenen degerine uygulanan bir disbukey fonksiyon her zaman rastgele degiskenin disbukey fonksiyonunun beklenen degeri ile ustten sinirlidir Jensen esitsizligi olarak bilinen bu sonuc ve Holder esitsizligi gibi esitsizlikleri cikarmak icin kullanilabilir TanimX displaystyle X gercel bir vektor uzayin disbukey altkumesi olsun ve f X R displaystyle f X to mathbb R bir fonksiyon olsun Asagida verilen ve birbirine denk olanr kosullardan biri f displaystyle f tarafindan saglandiginda f displaystyle f ye disbukey fonksiyon denir Her 0 t 1 displaystyle 0 leq t leq 1 ve her x1 x2 X displaystyle x 1 x 2 in X icin f tx1 1 t x2 tf x1 1 t f x2 displaystyle f left tx 1 1 t x 2 right leq tf left x 1 right 1 t f left x 2 right Esitsizligin sagindaki ifade f displaystyle f nin grafiginde x1 f x1 displaystyle left x 1 f left x 1 right right ve x2 f x2 displaystyle left x 2 f left x 2 right right arasindaki dogruyu t displaystyle t nin fonksiyonu olarak belirtir Soldaki ifadede ise f displaystyle f fonksiyonunun argumani X displaystyle X teki x1 displaystyle x 1 ve x2 displaystyle x 2 elemanlari arasindaki dogruyu belirtir Demek ki bu kosul ile f displaystyle f nin grafigindeki iki noktayi baglayan dogrunun ya grafigin uzerinde ya da ustunde olmasi istenmektedir Her 0 lt t lt 1 displaystyle 0 lt t lt 1 ve x1 x2 displaystyle x 1 neq x 2 saglayan butun x1 x2 X displaystyle x 1 x 2 in X icin f tx1 1 t x2 tf x1 1 t f x2 displaystyle f left tx 1 1 t x 2 right leq tf left x 1 right 1 t f left x 2 right Bu ikinci tanim sartinin birinci tanim sartindan temel farki alinan dogru ile grafigin kesismesini istememesidir Birinci kosulda t 1 displaystyle t 1 alirsak f x1 f x1 displaystyle f left x 1 right leq f left x 1 right t 0 displaystyle t 0 alirsak f x2 f x2 displaystyle f left x 2 right leq f left x 2 right olacaktir ki bu ifadeler zaten dogrudur Yine x1 x2 displaystyle x 1 x 2 alirsak her zaman dogru olan ifadeler ortaya cikar O yuzden bu kosullari tanimdan cikarmanin bir zarari yoktur Gercel sayi dogrusu R displaystyle mathbb R de deger alan disbukey fonksiyonlari karakterize eden ikinci ifade ayrica genisletilmis gercel sayi dogrusunda yani R displaystyle infty infty mathbb R cup pm infty kumesinde deger alan disbukey fonksiyonlari tanimlamak icin de kullanilan ifadedir Diger deyisle bir f displaystyle f fonksiyonu displaystyle pm infty degerleri aliyorsa o zaman ikinci ifadeyi kullanmak daha elverislidir Birinci ifadenin kullanilmamasinin ilk sebebi t displaystyle t nin 0 displaystyle 0 veya 1 displaystyle 1 degeri almasina izin verilmesidir ki bu durumda sirasiyla f x1 displaystyle f left x 1 right pm infty veya f x2 displaystyle f left x 2 right pm infty olursa 0 displaystyle 0 cdot infty and 0 displaystyle 0 cdot infty ifadelerinin tanimsizligindan dolayi tf x1 1 t f x2 displaystyle tf left x 1 right 1 t f left x 2 right ifadesi de tanimsiz olur Yine displaystyle infty infty ifadesi de tanimsizdir Bu yuzden genisletilmis gercel sayi dogrusunda deger alan disbukey fonksiyonlarin displaystyle infty ve displaystyle infty degerlerinden genelde sadece bir tanesini almasina izin verilir Kesin disbukeylik Ikinci ifade kesin disbukeyligin tanimini elde etmek icin de degistirilebilir ki burada esitlige de izin veren kucuk esittir gosterimi displaystyle leq yerini esitlige izin vermeyen kucuktur gosterimine lt displaystyle lt birakir Daha matematiksel bir ifadeyle her 0 lt t lt 1 displaystyle 0 lt t lt 1 ve x1 x2 displaystyle x 1 neq x 2 olan butun x1 x2 X displaystyle x 1 x 2 in X icin f tx1 1 t x2 lt tf x1 1 t f x2 displaystyle f left tx 1 1 t x 2 right lt tf left x 1 right 1 t f left x 2 right ozelligini saglayan fonksiyonlara kesin disbukey denir Kesin disbukey fonksiyonlarin grafigindeki iki farkli noktayi birlestiren dogru parcasinin uc noktalari haric geriye kalan butun noktalari fonksiyonun grafiginin ustunde kalir Disbukey olup da kesin disbukey olmayan bir fonksiyona f x y x2 y displaystyle f x y x 2 y ornegi verilebilir Bir fonksiyonun negatifi disbukeyse ya da kesin disbukeyse o zaman fonksiyona icbukey fonksiyon ya da kesin icbukey fonksiyon denir Disbukeyimsi fonksiyon Bir aralikta veya daha genel olarak vektor uzayindaki bir disbukey kumede tanimli ve gercel degerli bir f displaystyle f fonksiyonu eger her a 0 1 displaystyle alpha in 0 1 icin f 1 a x ay max f x f y displaystyle f 1 alpha x alpha y leq max f x f y esitsizligini tanim kumesindeki her x displaystyle x ve y displaystyle y icin sagliyorsa o zaman fonksiyona disbukeyimsi fonksiyon denir OzelliklerDisbukey fonksiyonlarin bircok ozelligi tek degiskenli fonksiyonlar icin oldugu gibi cok degiskenli fonksiyonlar icin de basitlikle ifade edilebilir ve genelde de ayni formulasyona sahiptir Bu yuzden cok degiskenli fonksiyonlar icin asagida verilen ozelliklere de bakiniz bu ozelliklerden bir degiskenli fonksiyonlar kisminda ayrica bahsedilmemistir Bir degiskenli fonksiyonlar Bir aralik uzerinde tanimli ve gercel degiskenli bir f displaystyle f fonksiyonunu ele alalim ve R x1 x2 f x2 f x1 x2 x1 displaystyle R x 1 x 2 frac f x 2 f x 1 x 2 x 1 fonksiyonunu tanimlayalim R displaystyle R fonksiyonunda x1 displaystyle x 1 ve x2 displaystyle x 2 nin yerleri degistirildiginde fonksiyonun degeri ayni kaldigi icin R displaystyle R fonksiyonu x1 x2 displaystyle x 1 x 2 degiskeninde olur O zaman f displaystyle f fonksiyonunun disbukeyligi icin gerekli ve yeterli sart R x1 x2 displaystyle R x 1 x 2 fonksiyonunun sabitlenmis x2 displaystyle x 2 degerleri icin x1 displaystyle x 1 degiskeninde olmasidir Bir C displaystyle C acik araligi uzerinde tanimli ve bir gercel degiskenli bir fonksiyon disbukeyse o zaman bu aralik uzerinde sureklidir Fonksiyonun ayni zamanda soldan ve sagdan turevleri de vardir ve turevler kesin azalmayandir Ayrica sol turev soldan surekli sag turev ise sagdan sureklidir Sonuc olarak fonksiyon en fazla sayilabilir bir kume haricinde turevlidir Yine de fonksiyonun turevli olmadigi noktalar yogun olabilir Eger C displaystyle C kapali araliksa C displaystyle C nin baslangic ve bitis noktalarinda fonksiyonun surekliligi olmayabilir Turevlenebilir bir fonksiyonun bir aralikta disbukey olmasi icin gerekli ve yeterli sart turevinin ayni aralikta kesin azalmayan olmasidir Bir fonksiyon hem disbukey hem de turevlenebilirse o zaman surekli turevlenebilirdir yani turevi de sureklidir Bir gercel degiskenli ve turevlenebilir bir fonksiyonun disbukey olmasi icin gerekli ve yeterli sart fonksiyonun grafiginin butun teget dogrularinin ustunde yer almasidir yani her x displaystyle x ve y displaystyle y icin f x f y f y x y displaystyle f x geq f y f y x y olmalidir Bir gercel degiskenli ve iki kere turevlenebilir bir fonksiyonun disbukey olmasi icin gerekli ve yeterli sart ikinci turevinin negatif olmamasidir Disbukey bir f displaystyle f fonksiyonu icin f 0 0 displaystyle f 0 leq 0 varsa o zaman butun pozitif a displaystyle a ve b displaystyle b icin f a b f a f b displaystyle f a b geq f a f b saglanir Kanit f displaystyle f disbukey oldugu icin disbukeylik taniminda x2 0 displaystyle x 2 0 alarak butun 0 t 1 displaystyle 0 leq t leq 1 icin f tx1 f tx1 1 t 0 tf x1 1 t f 0 tf x1 displaystyle begin aligned f tx 1 amp f tx 1 1 t cdot 0 amp leq tf x 1 1 t f 0 amp leq tf x 1 end aligned elde edilir f tx1 tf x1 displaystyle f tx 1 leq tf x 1 oldugu icin f a f b f a b aa b f a b ba b aa bf a b ba bf a b f a b displaystyle begin aligned f a f b amp f left a b frac a a b right f left a b frac b a b right amp leq frac a a b f a b frac b a b f a b amp f a b end aligned Boylece f a f b f a b displaystyle f a f b leq f a b olur Bir C displaystyle C araliginda tanimli f displaystyle f fonksiyonu her x1 x2 C displaystyle x 1 x 2 in C icin f x1 x22 f x1 f x2 2 displaystyle f left frac x 1 x 2 2 right leq frac f x 1 f x 2 2 ozelligini sagliyorsa bu fonksiyon orta nokta disbukeyligini sagliyordur Bu ozellik disbukeylikten daha zayif bir ozelliktir ve elbette butun disbukey fonksiyonlar bu ozelligi saglar Tersi yonde ise Sierpinski nin bir teoremi gecerlidir Orta nokta disbukeyligini saglayan butun Lebesgue olculebilir fonksiyonlar ayni zamanda disbukeydir Daha da ozelde surekli bir fonksiyon orta nokta disbukeyligini sagliyorsa disbukeydir Cok degiskenli fonksiyonlar Herbir degiskeninde ayri ayri disbukey olan bir fonksiyon genel olarak disbukey olmak zorunda degildir Mesela f x y xy displaystyle f x y xy fonksiyonu her bir degiskende digeri sabit tutularak dogrusalliktan dolayi disbukeydir ancak fonksiyonda tum degiskenler ayni anda hesaba katildiginda disbukey degildir Genisletilmis gercel sayilar dogrusu R displaystyle infty infty mathbb R cup pm infty kumesinde degerler alan bir f X displaystyle f X to infty infty fonksiyonunun disbukeyligi icin fonksiyonun x r X R r f x displaystyle x r in X times mathbb R r geq f x biciminde yazilabilen epigrafinin disbukey olmasi gerekli ve yeterlidir Turevlenebilir bir f displaystyle f fonksiyonunun disbukey olmasi icin f x f y f y T x y displaystyle f x geq f y nabla f y T cdot x y esitsizliginin fonksiyonun tanim kumesindeki butun x y displaystyle x y elemanlari icin saglanmasi gerekli ve yeterlidir Iki kere turevlenebilen bir fonksiyonun bir disbukey kume uzerinde disbukey olmasi icin Hesse matrisinin disbukey kumenin icinde kesin pozitif matris olmasi gerekli ve yeterlidir Bir f displaystyle f fonksiyonu disbukeyse o zaman a R displaystyle a in mathbb R icin x f x lt a displaystyle x f x lt a ve x f x a displaystyle x f x leq a disbukey kumedir Bu tur ozellikleri saglayan fonksiyonlara adi verilir ve her zaman disbukey olmayabilirler Bir disbukey fonksiyonun yerel minimumu ayni zamanda mutlak minimumudur Kesin disbukey fonksiyonun en fazla bir tane mutlak minimumu olabilir Jensen esitsizligi butun disbukey fonksiyonlara uygulanabilir Eger X displaystyle X ile gosterilen bir rassal degiskenin deger kumesi disbukey bir f displaystyle f fonksiyonunun tanim kumesindeyse E f X f E X displaystyle operatorname E f X geq f operatorname E X olur Burada E displaystyle operatorname E beklenen degerdir Gercekten de Jensen esitsizliginin hipotezini saglayan fonksiyonlar disbukey fonksiyonlardir f ax ay af x y displaystyle f ax ay af x y esitligini butun a x y gt 0 displaystyle a x y gt 0 icin saglayan birinci mertebeden iki degiskenli homojen fonksiyonlar bir degiskeninde disbukey ise diger degiskende de disbukeydir Disbukeyligi koruyan islemlerBir f displaystyle f fonksiyonun disbukeyligi f displaystyle f fonksiyonunun icbukeyligine denktir Herhangi bir r displaystyle r gercel sayisi icin r f displaystyle r f ancak ve ancak f displaystyle f disbukeyse disbukeydir w1 wn 0 displaystyle w 1 ldots w n geq 0 ise ve f1 fn displaystyle f 1 ldots f n fonksiyonlarinin hepsi disbukeyse o zaman w1f1 wnfn displaystyle w 1 f 1 cdots w n f n de disbukeydir Ozellikle iki disbukey fonksiyonun toplami yine disbukeydir Bu ozellik tanimli olduklari surece sonsuz toplamlara integrallere ve beklenen degerlere de genisletilebilir Disbukey fonksiyonlarin bir noktadaki supremumu uzerinden tanimlanan fonksiyon da disbukeydir Diger deyisle I displaystyle I bir endis kumesi ise ve fi i I displaystyle f i i in I kumeleri de bu fonksiyonlarin bu endis kumesine gore disbukey bir ailesi ise o zaman g x supi Ifi x displaystyle g x sup nolimits i in I f i x fonksiyonu da disbukeydir Bu ozelligin ozel bir durumu olarak Disbukey fonksiyonlarin maksimumu yine disbukeydir Yani f1 fn displaystyle f 1 ldots f n disbukey fonksiyonlar ise o zaman g x max f1 x fn x displaystyle g x max left f 1 x ldots f n x right fonksiyonu da disbukeydir f x y displaystyle f x y fonksiyonu x displaystyle x degiskeninde disbukey ise o zaman g x supy Cf x y displaystyle g x sup nolimits y in C f x y fonksiyonu da C displaystyle C kumesi disbukey olmasa bile disbukeydir f x y displaystyle f x y fonksiyonu x y displaystyle x y degiskeninde disbukeyse o zaman g x infy Cf x y displaystyle g x inf nolimits y in C f x y fonksiyonu x displaystyle x degiskeninde C displaystyle C kumesi disbukey ve g x displaystyle g x neq infty oldugu surece disbukeydir f displaystyle f ve g displaystyle g fonksiyonlari disbukey fonksiyonlar ise ve g displaystyle g gercel dogru uzerindeki bir kumede azalmiyor ise o zaman h x g f x displaystyle h x g f x fonksiyonu da disbukeydir Ornegin f displaystyle f disbukeyse ef x displaystyle e f x de disbukeydir cunku ex displaystyle e x disbukeydir ve kesin artandir Benzer bir ozellik ise su durumda cikar Eger f displaystyle f icbukeyse g displaystyle g disbukeyse ve g displaystyle g gercel dogru uzerindeki bir kumede artmiyor ise o zaman h x g f x displaystyle h x g f x de disbukeydir Disbukeylik afin gonderimler altinda degismez bir ozellige sahiptir Diger deyisle f displaystyle f fonksiyonu bir Df Rm displaystyle D f subseteq mathbf R m kumesi uzerinde disbukey ise o zaman g x f Ax b displaystyle g x f Ax b kumesi de disbukeydir Burada A Rm n b Rm displaystyle A in mathbf R m times n b in mathbf R m ve g displaystyle g nin tanim kumesi Dg Rn displaystyle D g subseteq mathbf R n alinmistir f displaystyle f disbukeyse tanim kumesi x t xt Dom f t gt 0 displaystyle left x t tfrac x t in operatorname Dom f t gt 0 right olan g x t tf xt displaystyle g x t tf left tfrac x t right fonksiyonu da disbukeydir X displaystyle X bir vektor uzayi olsun f X R displaystyle f X to mathbf R fonksiyonun disbukey olmasi ve f 0 0 displaystyle f 0 leq 0 esitsizligini saglamasi ancak ve ancak x y X displaystyle x y in X ve a b 1 displaystyle a b leq 1 ozelligini saglayan her a b 0 displaystyle a b geq 0 icinf ax by af x bf y displaystyle f ax by leq af x bf y ozelligi saglaniyorsa mumkundur Guclu disbukey fonksiyonlarKesin disbukeylik kavramini bir paramatre araciligiyla genellestiren guclu disbukeylik kavrami da mevcuttur Sezgisel olarak guclu disbukey bir fonksiyon en az ikinci dereceden bir fonksiyon kadar hizli buyuyen bir fonksiyondur Guclu disbukey bir fonksiyon kesin disbukeydir ancak bu ifadenin tersi her zaman dogru degildir Tek gercel degiskene bagli ve tanim kumesi reel sayi dogrusu olan bir f displaystyle f fonksiyonu iki kez surekli turevlenebilirse disbukeyligi su sekilde karakterize edebilir f displaystyle f nin disbukeyligi ancak ve ancak her x displaystyle x icin f x 0 displaystyle f x geq 0 ise mumkundur Her x displaystyle x icin f x gt 0 displaystyle f x gt 0 ise f displaystyle f kesin disbukeydir ancak bu yeterli bir kosuldur ve gerekli degildir f displaystyle f nin guclu disbukeyligi ancak ve ancak her x displaystyle x icin f x m gt 0 displaystyle f x geq m gt 0 saglayan pozitif gercel bir m displaystyle m sayisi ile mumkundur Ornegin f displaystyle f kesin disbukey olsun ve diyelim ki f xn 1n displaystyle f x n tfrac 1 n ozelliginin saglandigi bir xn displaystyle x n noktalar dizisi olsun f xn gt 0 displaystyle f x n gt 0 olmasina ragmen fonksiyon yine de guclu disbukey degildir cunku f x displaystyle f x keyfi olarak kucuk olup sifira yaklasacaktir Daha genel olarak turevlenebilir bir f displaystyle f fonksiyonunun bir m gt 0 displaystyle m gt 0 parametresi araciligiyla guclu disbukeyligi su sekilde tanimlanabilir Fonksiyonun tanim kumesindeki her x y displaystyle x y sayisi icin f x f y T x y m x y 22 displaystyle nabla f x nabla f y T x y geq m x y 2 2 saglaniyorsa fonksiyona guclu disbukey denilir Daha genel bir ifadeyle displaystyle langle cdot cdot rangle herhangi bir ic carpimi temsil etsin ve displaystyle cdot ise bu ic carpim tarafindan dogurulan bir norm olsun f displaystyle f fonksiyonunun tanim kumesindeki her x y displaystyle x y sayisi icin f x f y x y m x y 2 displaystyle langle nabla f x nabla f y x y rangle geq m x y 2 saglaniyorsa fonksiyona guclu disbukey denilir Bazi yazarlar ornegin bu esitsizligi saglayan fonksiyonlara olarak da adlandirirlar Yukarida verilen sartlara esdeger bir sart da soyle tanimlanabilir f y f x f x T y x m2 y x 22 displaystyle f y geq f x nabla f x T y x frac m 2 y x 2 2 Bir fonksiyonun guclu disbukey olmasi icin turevlenebilir olmasi gerekli degildir Bir fonksiyonun m displaystyle m parametreli guclu disbukeyliligi icin ucuncu bir tanim soyle verilebilir tanim kumesindeki her x y displaystyle x y ve her t 0 1 displaystyle t in 0 1 icin f tx 1 t y tf x 1 t f y 12mt 1 t x y 22 displaystyle f tx 1 t y leq tf x 1 t f y frac 1 2 mt 1 t x y 2 2 saglaniyorsa fonksiyon m displaystyle m parametreli guclu disbukeydir Gercekten de m 0 displaystyle m to 0 iken tanim guclu disbukeylilik tanimina yaklasmaktadir ve m 0 displaystyle m 0 oldugugunda da disbukeylik tanimina ozdestir Yine de herhangi bir m gt 0 displaystyle m gt 0 sayisi icin kesin disbukey olup da guclu disbukey olmayan fonksiyonlar da vardir Bir f displaystyle f fonksiyonu iki kez turevlenebilirse o zaman bir m displaystyle m parametresine bagli guclu disbukeyliligi ancak ve ancak tanim kumesindeki her x displaystyle x icin 2f x mI displaystyle nabla 2 f x succeq mI ise mumkundur Burada I displaystyle I birim matristir 2f displaystyle nabla 2 f ise Hesse matrisidir displaystyle succeq ile kastedilen ise 2f x mI displaystyle nabla 2 f x mI matrisinin olmasidir ki bu da her x displaystyle x icin 2f x displaystyle nabla 2 f x matrisinin en kucuk ozdegerinin en az m displaystyle m olmasi demektir Eger tanim kumesi gercel sayi dogrusu ise 2f x displaystyle nabla 2 f x ifadesi ikinci tureve denk gelir Boylece guclu disbukeylilik icin gerekli ve yeterli sart f x m displaystyle f x geq m olmasidir m 0 displaystyle m 0 olursa o zaman bu durumda Hesse matrisi yari kesin pozitif matris olur ya da tanim kumesi gercel dogru ise f x 0 displaystyle f x geq 0 olur ki bu durumda da fonksiyon disbukey olur Ayni durumda fonksiyon kesin disbukey olabilir ama guclu disbukey degildir Fonksiyonun iki kez surekli olarak turevlenebilir oldugunu varsayarak 2f x displaystyle nabla 2 f x ifadesinin alt sinirinin guclu disbukeyliligi verdigini su sekilde gosterilebiliriz Taylor teoremi kullanarak f y f x f x T y x 12 y x T 2f z y x displaystyle f y f x nabla f x T y x frac 1 2 y x T nabla 2 f z y x esitligini saglayan bir z tx 1 t y t 0 1 displaystyle z in tx 1 t y t in 0 1 bulunabilir Ozdeger varsayimindan hareketle y x T 2f z y x m y x T y x displaystyle y x T nabla 2 f z y x geq m y x T y x elde edilir Yukaridaki esitlik kullanilarak yukaridaki ikinci guclu disbukeylik kosulunun saglandigi gosterilmis olur Yine bir f displaystyle f fonksiyonunun m displaystyle m parametresine bagli guclu disbukeyliligi x f x m2 x 2 displaystyle x mapsto f x frac m 2 x 2 gonderiminin disbukeyliligi araciligiyla da tanimlanabilir Tanim kumesi tikiz bir X displaystyle X olan ve iki kez surekli turevlenebilen bir f displaystyle f fonksiyonu icin f x gt 0 displaystyle f x gt 0 ifadesi her x X displaystyle x in X icin saglaniyorsa o zaman f displaystyle f fonksiyonu guclu disbukeydir Bu sonucun ispati tikiz bir kume uzerinde surekli bir fonksiyonun bir maksimum ve bir minimuma sahip oldugunu belirten kullanilarak verilebilir Guclu disbukey fonksiyonlar sinifi daha kucuk oldugu icin bu tur fonksiyonlarla calisilmasi disbukey veya kesin disbukey fonksiyonlara gore genellikle daha kolaydir Kesin disbukey fonksiyonlar gibi guclu disbukey fonksiyonlarin da tikiz kumelerde biricik minimumu vardir Guclu disbukey fonksiyonlarin ozellikleri Bir m displaystyle m parametresine bagli guclu disbukey olan bir f displaystyle f fonksiyonunu ele alalim O zaman Tum gercel r displaystyle r sayilari icin x f x r displaystyle x f x leq r f displaystyle f fonksiyonun Rn displaystyle mathbb R n uzerinde bir mutlak ve biricik minimumu vardir Duzgun disbukey fonksiyonlarϕ displaystyle phi negatif olmayan ve ϕ 0 0 displaystyle phi 0 0 olan bir fonksiyon olsun Bir f displaystyle f fonksiyonu tanim kumesindeki her x y displaystyle x y ve her t 0 1 displaystyle t in 0 1 icin f tx 1 t y tf x 1 t f y t 1 t ϕ x y displaystyle f tx 1 t y leq tf x 1 t f y t 1 t phi x y ozelligini sagliyorsa f displaystyle f ye modulu ϕ displaystyle phi olan duzgun disbukey fonksiyon denir ϕ a m2a2 displaystyle phi alpha tfrac m 2 alpha 2 alarak guclu disbukeylik tanimi buradan elde edilebildigi icin bu tanim guclu disbukeyligin daha genel bir tanimi olmaktadir Literaturde bazi yazarlar ϕ displaystyle phi fonksiyonunun artan olmasini da kosul olarak koyarlar ancak yine de bu kosul her yazar tarafindan benimsenmemistir OrneklerBir degiskenli fonksiyonlar f x x2 displaystyle f x x 2 fonksiyonu icin f x 2 gt 0 displaystyle f x 2 gt 0 elde edilir Bu yuzden f disbukey fonksiyondur Ayni zamanda guclu disbukeydir ki bu yuzden kesin disbukeydir guclu disbukeylik parametresi de 2 olur f x x4 displaystyle f x x 4 fonksiyonu icin f x 12x2 0 displaystyle f x 12x 2 geq 0 olur Bu yuzden f disbukey fonksiyondur Ikinci turevi bir noktada sifir degeri alsa da fonksiyon yine de kesin disbukeydir Ancak fonksiyon guclu disbukey degildir Mutlak deger fonksiyonu disbukeydir ki gosterimi ucgen esitsizliginden kolaylikla elde edilir Fonksiyonun grafiginde x 0 displaystyle x 0 noktasinde gorulen sivri uc turevin varligina engeldir Ayrica fonksiyon kesin disbukey degildir f x x p displaystyle f x x p fonksiyonu p 1 displaystyle p geq 1 icin disbukeydir Ustel fonksiyon f x ex displaystyle f x e x disbukeydir f x ex gt 0 displaystyle f x e x gt 0 oldugu icin kesin disbukeydir Ancak ikinci turev sifira keyfi derecede yakin oldugu icin guclu disbukey degildir Daha genel olarak f displaystyle f fonksiyonu disbukey oldugunda g x ef x displaystyle g x e f x fonksiyonu logaritmik disbukey fonksiyon olur 0 1 displaystyle 0 1 araliginda f 0 f 1 1 f x 0 displaystyle f 0 f 1 1 f x 0 olarak tanimli fonksiyon 0 lt x lt 1 displaystyle 0 lt x lt 1 araliginda disbukeydir 0 1 displaystyle 0 1 acik araliginda sureklidir ama 0 and 1 noktalarinda sureklilik yoktur x3 displaystyle x 3 fonksiyonunun ikinci turevi 6x displaystyle 6x olur Bu yuzden x 0 displaystyle x geq 0 olan noktalarda disbukeydir x 0 displaystyle x leq 0 olan noktalarda ise icbukeydir Kesin artan ve disbukey olmayan fonksiyonlara f x x displaystyle f x sqrt x ve g x log x displaystyle g x log x fonksiyonlari ornek olarak verilebilir f x 1x displaystyle f x tfrac 1 x fonksiyonun ikinci turevi f x 2x3 displaystyle f x tfrac 2 x 3 olur x gt 0 displaystyle x gt 0 iken ikinci turev pozitif olur boylece 0 displaystyle 0 infty araliginda f x displaystyle f x disbukeydir 0 displaystyle infty 0 araliginda ise fonksiyon icbukeydir f x 1x2 displaystyle f x tfrac 1 x 2 fonksiyonu f 0 displaystyle f 0 infty olarak tanimlansin O zaman fonksiyon 0 displaystyle 0 infty ve 0 displaystyle infty 0 araliklarinda disbukeydir Ancak displaystyle infty infty araliginda fonksiyonun disbukeyliginden bahsedilemez cunku x 0 displaystyle x 0 nokasindaki tekillik bu disbukeylik ozelligine izin vermez Cok degiskenli fonksiyonlar fonksiyonu disbukeydir olan X displaystyle X icin log det X displaystyle log det X fonksiyonu disbukeydir Gercel degerli her dogrusal donusum disbukeydir ama kesin disbukey degildir Gercekten f displaystyle f dogrusalsa o zaman f a b f a f b displaystyle f a b f a f b olur Ayni ifade disbukeyligi icbukeylikle degistirdigimizde de dogrudur Gercel degerli her yani f x aTx b displaystyle f x a T x b bicimindeki fonksiyonlar hem disbukey hem de icbukeydir ucgen esitsizligi ve ozelligi sayesinde disbukeydir kosegen elemanlarinin disbukey fonksiyonudur Ayrica bakinizIcbukey fonksiyon Hermite Hadamard esitsizligi Jensen esitsizligi Kacurovskiy teoremi Karamata esitsizligi Logaritmik disbukey fonksiyonKaynakca Lecture Notes 2 PDF www stat cmu edu 6 Mayis 2021 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 3 Mart 2017 Concave Upward and Downward 18 Aralik 2013 tarihinde kaynagindan arsivlendi disbukeyimsi fonksiyon Turkce Bilim Terimleri Sozlugu Turkiye Bilimler Akademisi Erisim tarihi 06 Aralik 2024 Boyd Stephen P Vandenberghe Lieven 2004 Convex Optimization pdf Cambridge University Press ISBN 978 0 521 83378 3 9 Mayis 2021 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 15 Ekim 2011 Donoghue William F 1969 Distributions and Fourier Transforms Academic Press s 12 ISBN 9780122206504 Erisim tarihi 29 Agustos 2012 If f is strictly convex in a convex set show it has no more than 1 minimum Math StackExchange 21 Mart 2013 28 Temmuz 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 14 Mayis 2016 Altenberg L 2012 Resolvent positive linear operators exhibit the reduction phenomenon Proceedings of the National Academy of Sciences 109 10 pp 3705 3710 Strong convexity Xingyu Zhou s blog xingyuzhou org 12 Nisan 2024 tarihinde kaynagindan arsivlendi Erisim tarihi 27 Eylul 2023 Dimitri Bertsekas 2003 Convex Analysis and Optimization Contributors Angelia Nedic and Asuman E Ozdaglar Athena Scientific s 72 ISBN 9781886529458 Philippe G Ciarlet 1989 Introduction to numerical linear algebra and optimisation Cambridge University Press ISBN 9780521339841 a b Yurii Nesterov 2004 Introductory Lectures on Convex Optimization A Basic Course Kluwer Academic Publishers ss 63 64 ISBN 9781402075537 Nemirovsky and Ben Tal 2023 Optimization III Convex Optimization PDF 10 Aralik 2023 tarihinde kaynagindan PDF arsivlendi a b C Zalinescu 2002 Convex Analysis in General Vector Spaces World Scientific ISBN 9812380671 a b H Bauschke and P L Combettes 2011 Convex Analysis and Monotone Operator Theory in Hilbert Spaces Springer s 144 ISBN 978 1 4419 9467 7
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State