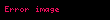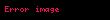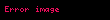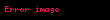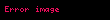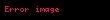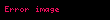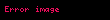Black-Scholes denklemi, 1973 yılında Fischer Black ve Myron Scholes tarafından yazılan makalede elde edilen Black-Scholes formülünün kanıtında ilk defa elde edilmiş ve daha genel türev ürünleri için de uyarlanabilen bir kısmi diferensiyel denklemdir. Black-Scholes formülünün orijinal kanıtındaki esas fikir, opsiyon ve opsiyon dayanak varlığından oluşan bir portföy yaratmak ve bu portföyü küçük zaman aralıklarında dayanak varlığın piyasa fiyatına duyarsız hale getirmektir. Sonucunda, Black-Scholes denklemi elde edilir ve elde edilen diferansiyel denklem, değişik dönüşümler ve yerine koymalar vasıtasıyla ısı denklemine dönüştürülür.
Denklemin ifadesi
Kullanma fiyatı K, vadesi T olan Avrupa tipi bir opsiyonun fiyatı 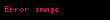



olsun. O zaman,
Kanıt
Black-Scholes modelinin merkezi varsayımlarından biri söz konusu dayanak varlığın (Black-Scholes özelinde hisse senedinin) fiyatının hareketlerinin (St) geometrik Brown hareketini izlemesidir. Yani, sabit bir sürüklenme (

Black-Scholes'un makalesindeki fikirden hareketle portföy (
- -1 tane opsiyon (yani opsiyon satılmıştır)
sonradan belirlenmek üzere
tane dayanak varlık
Opsiyonun fiyatı 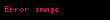
olur. Bu potrföyün değerinin kısa bir zaman aralığındaki değişimi 
olur. Öbür taraftan, fiyatı iki kere türevlenebilien bir türev ürününün fiyatı 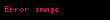
.
O zaman,
olur. Bu portföyün dayanak varlığın piyasa fiyatına duyarsız halde olması istendiğinden, difüzyon teriminin (rassallığa katkıda bulunan terimlerin) 0 olması gerekir. Yani, 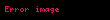
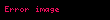
elde edilir. Diğer taraftan, portföy rassallığa duyarsız hale geldiği için ile büyüyecektir; yani,
elde edilir. 
Bu denklemin çözülmesi için aynı zamanda bir sınır değeri konulması lazım;ancak, zaten opsiyonun vade tarihindeki değeri opsiyonun türüne göre 
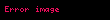
Ayrıca bakınız
Kaynakça
- ^ Black, Fischer; Scholes, Myron (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy. 81 (3): 637-654. doi:10.1086/260062. [1] 31 Mart 2024 tarihinde Wayback Machine sitesinde arşivlendi. (Black ve Scholes'un orijinal makalesi.)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Black Scholes denklemi 1973 yilinda Fischer Black ve Myron Scholes tarafindan yazilan makalede elde edilen Black Scholes formulunun kanitinda ilk defa elde edilmis ve daha genel turev urunleri icin de uyarlanabilen bir kismi diferensiyel denklemdir Black Scholes formulunun orijinal kanitindaki esas fikir opsiyon ve opsiyon dayanak varligindan olusan bir portfoy yaratmak ve bu portfoyu kucuk zaman araliklarinda dayanak varligin piyasa fiyatina duyarsiz hale getirmektir Sonucunda Black Scholes denklemi elde edilir ve elde edilen diferansiyel denklem degisik donusumler ve yerine koymalar vasitasiyla isi denklemine donusturulur Denklemin ifadesiKullanma fiyati K vadesi T olan Avrupa tipi bir opsiyonun fiyati V V t S displaystyle V V t S bu opsiyonun dayanak varliginin spot fiyati S oynakligi volatilitesi s displaystyle sigma ve risksiz faiz orani r olsun Diyelim ki dayanak varligin spot fiyat sureci geometrik Brown hareketini izlesin yani Brown hareketini W displaystyle W ile gosterirsek m displaystyle mu sabitse dSt mStdt sStdWt displaystyle dS t mu S t dt sigma S t dW t olsun O zaman V t rS V S S2s22 2V S2 rV 0 displaystyle frac partial V partial t rS frac partial V partial S frac S 2 sigma 2 2 frac partial 2 V partial S 2 rV 0 KanitBlack Scholes modelinin merkezi varsayimlarindan biri soz konusu dayanak varligin Black Scholes ozelinde hisse senedinin fiyatinin hareketlerinin St geometrik Brown hareketini izlemesidir Yani sabit bir suruklenme m displaystyle mu ve volatilite s displaystyle sigma olmak uzere dSt mStdt sStdWt displaystyle dS t mu S t dt sigma S t dW t Black Scholes un makalesindeki fikirden hareketle portfoy P displaystyle P su sekilde olussun 1 tane opsiyon yani opsiyon satilmistir displaystyle triangle sonradan belirlenmek uzere displaystyle triangle tane dayanak varlik Opsiyonun fiyati V V t S displaystyle V V t S olsun O zaman bu portfoyun degeri P V S displaystyle P V triangle S olur Bu potrfoyun degerinin kisa bir zaman araligindaki degisimi dP displaystyle mathrm d P o zaman dP dV dS displaystyle mathrm d P mathrm d V triangle mathrm d S olur Obur taraftan fiyati iki kere turevlenebilien bir turev urununun fiyati V V t S displaystyle V V t S icin Ito onsavi kullanilarak dV V t mS V S 12s2S2 2V S2 dt sS V SdW displaystyle mathrm d V left frac partial V partial t mu S frac partial V partial S frac 1 2 sigma 2 S 2 frac partial 2 V partial S 2 right mathrm d t sigma S frac partial V partial S mathrm d W O zaman dP dV dS V t mS V S 12s2S2 2V S2 mSt dt sS V S sS dW displaystyle mathrm d P mathrm d V triangle mathrm d S left frac partial V partial t mu S frac partial V partial S frac 1 2 sigma 2 S 2 frac partial 2 V partial S 2 triangle mu S t right mathrm d t left sigma S frac partial V partial S triangle sigma S right mathrm d W olur Bu portfoyun dayanak varligin piyasa fiyatina duyarsiz halde olmasi istendiginden difuzyon teriminin rassalliga katkida bulunan terimlerin 0 olmasi gerekir Yani sS V S sS 0 displaystyle sigma S frac partial V partial S triangle sigma S 0 olmalidir ki bu da V S displaystyle triangle frac partial V partial S verir O zaman dP V t 12s2S2 2V S2 dt displaystyle mathrm d P left frac partial V partial t frac 1 2 sigma 2 S 2 frac partial 2 V partial S 2 right mathrm d t elde edilir Diger taraftan portfoy rassalliga duyarsiz hale geldigi icin ile buyuyecektir yani dP rPdt rVdt rS V Sdt displaystyle mathrm d P rPdt rVdt rS frac partial V partial S dt elde edilir dP displaystyle mathrm d P icin elde edilen bu iki ifade birbirine esitlenerek Black Scholes kismi diferansiyel denklemi elde edilir V t rS V S S2s22 2V S2 rV 0 displaystyle frac partial V partial t rS frac partial V partial S frac S 2 sigma 2 2 frac partial 2 V partial S 2 rV 0 Bu denklemin cozulmesi icin ayni zamanda bir sinir degeri konulmasi lazim ancak zaten opsiyonun vade tarihindeki degeri opsiyonun turune gore max ST K 0 displaystyle max S T K 0 veya max K ST 0 displaystyle max K S T 0 olacaktir Ayrica bakinizFeynman Kac formuluKaynakca Black Fischer Scholes Myron 1973 The Pricing of Options and Corporate Liabilities Journal of Political Economy 81 3 637 654 doi 10 1086 260062 1 31 Mart 2024 tarihinde Wayback Machine sitesinde arsivlendi Black ve Scholes un orijinal makalesi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State