Çarpı

Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.

Bu maddenin veya maddenin bir bölümünün gelişebilmesi için konusunda uzman kişilere gereksinim duyulmaktadır.
Ayrıntılar için lütfen inceleyin veya yeni bir tartışma başlatın.
Konu hakkında uzman birini bulmaya yardımcı olarak ya da maddeye gerekli bilgileri Vikipedi'ye katkıda bulunabilirsiniz.
(Mayıs 2015)

Çarpma, temel aritmetik işlemlerden biridir. Sayılarda çarpma, çarpılan sayının çarpan sayı kadar adedinin toplamının alınması işlemidir.

45 x 256 = 11.520 işleminin Çin metodu ile çözümü. Bu yöntemde çarpılacak sayılar basamaklarına ayrılarak sütun ve satır başlarına yazılır. Her bir kutu çaprazlamasına ikiye bölünür. Satır ile sütunların çarpımları iki üçgen bölüme yerleştirilir. Örneğin şekilde 5 ve 2'nin çarpımı 1 ve 0 olarak ilk iki üçgene yerleştirilmiştir. Daha sonra çapraz kolonlar toplanır. Örneğin 5 + 3 + 4 = 12 işleminin birler basamağı olan 2 rakamı en sağa yazılmıştır ve 1 rakamı hemen solundaki çapraz kolona devretmiştir. Toplamalar da tamamlandıktan sonra soldan sağa en dıştaki rakamlar (koyu yazılanlar) işlemin sonucunu verir.

{{a\times n=} \atop {\ }}{{\underbrace {a+\cdots +a} } \atop n}

Örneğin 5 ile 4 sayılarının çarpılması demek 4 adet 5 sayısının toplanması veya değişme özelliği uyarınca (aşağıda anlatıldığı üzere) 5 adet 4 sayısının toplanması anlamına gelir. Matematiksel olarak ifade etmek gerekirse: "5 * 4 = 5 + 5 + 5 + 5" ya da "5 * 4 = 4 + 4 + 4 + 4 + 4".

Sayılarla değil, örneğin matrislerle ilgilenirken çarpma işleminin tanımı ve uygulaması farklılık gösterir.

Cebirsel ifadelerde x harfi değişken olarak kullanıldığından, cebirsel ifade sorularında ''x'' yerine ''.'' kullanılabilir.

Sayılarda çarpmanın özellikleri

tamsayılar kümesi, , . Çarpma, bu halkanın ikinci işlemidir. kümesi ise bir cisimdir ve çarpma bu cismin ikinci işlemidir. Tanım gereği bazı matematiksel özelliklere sahiptir.

Kapalılık özelliği

İki tam/kesirli sayının çarpımı yine bir tam/kesirli sayıdır.

Birleşme özelliği

Üç tam/kesirli sayının çarpımında, işlemin yan yana hangi ikiliden başladığı sonucu değiştirmez, yani herhangi x, y, z tam/kesirli sayıları için: $(x.y).z=x.(y.z)$

Etkisiz eleman

1 (bir) sayısı, tam/kesirli sayılar kümesinde çarpma işlemine göre etkisiz elemandır.

$x.1=x$

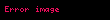
Ters elemanlar

Tam sayılar kümesinde 1 ve -1 hariç hiçbir elemanın çarpmaya göre tersi yoktur. Kesirli sayılar kümesinde çarpma işlemine göre, 0 hariç her elemanın tersi vardır.

Her x için, 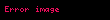$x.1/x=1$

Değişme özelliği

İki tam/kesirli sayının çarpımında, elemanların yerleri değiştirildiğinde sonuç değişmez.

$x.y=y.x$

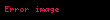
Dağılma özelliği

Çarpma işleminin toplama işlemi üzerine dağılma özelliği vardır.

$x.(y+z)=x.y+x.z$

Yutan Eleman

Yutan eleman herhangi bir matematiksel işlemde, işlemin sonucunu kendisine dönüştüren elemandır. Çarpma işleminde sıfır (0) sayısı yutan elemandır zira sıfırın herhangi bir sayıyla çarpımı sıfıra eşittir:

$x.0=0$

Yutan eleman, yalnızca tam ve kesirli sayılarda değil, herhangi bir halkada sıfırdan başka bir eleman olamaz. Bu nedenle örtüşür.

Kaynakça

wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar

Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu maddenin veya maddenin bir bolumunun gelisebilmesi icin matematik konusunda uzman kisilere gereksinim duyulmaktadir Ayrintilar icin lutfen tartisma sayfasini inceleyin veya yeni bir tartisma baslatin Konu hakkinda uzman birini bulmaya yardimci olarak ya da maddeye gerekli bilgileri ekleyerek Vikipedi ye katkida bulunabilirsiniz Mayis 2015 Carpma temel aritmetik islemlerden biridir Sayilarda carpma carpilan sayinin carpan sayi kadar adedinin toplaminin alinmasi islemidir 45 x 256 11 520 isleminin Cin metodu ile cozumu Bu yontemde carpilacak sayilar basamaklarina ayrilarak sutun ve satir baslarina yazilir Her bir kutu caprazlamasina ikiye bolunur Satir ile sutunlarin carpimlari iki ucgen bolume yerlestirilir Ornegin sekilde 5 ve 2 nin carpimi 1 ve 0 olarak ilk iki ucgene yerlestirilmistir Daha sonra capraz kolonlar toplanir Ornegin 5 3 4 12 isleminin birler basamagi olan 2 rakami en saga yazilmistir ve 1 rakami hemen solundaki capraz kolona devretmistir Toplamalar da tamamlandiktan sonra soldan saga en distaki rakamlar koyu yazilanlar islemin sonucunu verir a n a a n displaystyle a times n atop underbrace a cdots a atop n Ornegin 5 ile 4 sayilarinin carpilmasi demek 4 adet 5 sayisinin toplanmasi veya degisme ozelligi uyarinca asagida anlatildigi uzere 5 adet 4 sayisinin toplanmasi anlamina gelir Matematiksel olarak ifade etmek gerekirse 5 4 5 5 5 5 ya da 5 4 4 4 4 4 4 Sayilarla degil ornegin matrislerle ilgilenirken carpma isleminin tanimi ve uygulamasi farklilik gosterir Cebirsel ifadelerde x harfi degisken olarak kullanildigindan cebirsel ifade sorularinda x yerine kullanilabilir Sayilarda carpmanin ozellikleritamsayilar kumesi Carpma bu halkanin ikinci islemidir kumesi ise bir cisimdir ve carpma bu cismin ikinci islemidir Tanim geregi bazi matematiksel ozelliklere sahiptir Kapalilik ozelligi Iki tam kesirli sayinin carpimi yine bir tam kesirli sayidir Birlesme ozelligi Uc tam kesirli sayinin carpiminda islemin yan yana hangi ikiliden basladigi sonucu degistirmez yani herhangi x y z tam kesirli sayilari icin x y z x y z displaystyle x y z x y z Etkisiz eleman 1 bir sayisi tam kesirli sayilar kumesinde carpma islemine gore etkisiz elemandir x 1 x displaystyle x 1 x Ters elemanlar Tam sayilar kumesinde 1 ve 1 haric hicbir elemanin carpmaya gore tersi yoktur Kesirli sayilar kumesinde carpma islemine gore 0 haric her elemanin tersi vardir Her x icin x 1 x 1 displaystyle x 1 x 1 Degisme ozelligi Iki tam kesirli sayinin carpiminda elemanlarin yerleri degistirildiginde sonuc degismez x y y x displaystyle x y y x Dagilma ozelligi Carpma isleminin toplama islemi uzerine dagilma ozelligi vardir x y z x y x z displaystyle x y z x y x z Yutan Eleman Yutan eleman herhangi bir matematiksel islemde islemin sonucunu kendisine donusturen elemandir Carpma isleminde sifir 0 sayisi yutan elemandir zira sifirin herhangi bir sayiyla carpimi sifira esittir x 0 0 displaystyle x 0 0 Yutan eleman yalnizca tam ve kesirli sayilarda degil herhangi bir halkada sifirdan baska bir eleman olamaz Bu nedenle ortusur Kaynakca

Bu maddede birçok sorun bulunmaktadır Lütfen sayfayı geliştirin veya bu sorunlar konusunda tartışma sayfasında bir yorum