Matematikte zayıf türev, güçlü türev olarak da bilinen olağan türev kavramının bir genellemesidir. Zayıf türev kavramı türevlenebilir olmadığı ama bir Lebesgue uzayında olduğu varsayılan fonksiyonlar için geliştirilmiş bir türev kavramıdır.
Zayıf türev kavramı aynı zamanda kavramının tanımlanmasına da yol açar.
Tanım
Tanımın arkasında yatan ana fikir bir Lebesgue uzayı içindeki sonsuz türevli ve sahip fonksiyonların bu uzay içinde yoğun olarak var olması gerçeğine dayanır. Gerçekten de, türevlenebilir 

elde edilir. 



elde edilir. Tıkız desteğe sahip sonsuz türevli 

Basit tanım
Gerçel sayılar üzerindeki bir 




eşitliğini sağlayan bir 



Genel tanım
Öklid uzayındaki açık bir 











elde edilir.
bir 






eşitliğini sağlayan bir 



Özellikler
Bir 


Güçlü türevi Lebesgue uzayında yer alan bir 
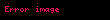

İlk önce zayıf türev tanımı gereği, sonsuz türevli ve tıkız destekli harhangi bir 
olacaktır. 
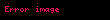

yazarak, 

olur. Bu yüzden, sonsuz türevli ve tıkız destekli harhangi bir 
olur ki bu da noktasal olarak hemen hemen her yerde 

Örnekler







Rasyonel sayıların karakteristik fonksiyonu 






Zayıf türev kavramı türevliliği genelleştirmez. Diğer deyişle, hemen hemen her yerde türevi olan bir fonksiyonun zayıf türevi olmayabilir. Örneğin, 

Ayrıca bakınız
Kaynakça
- ^ a b c Evans, Lawrence C. (1998). Partial differential equations. Providence, R.I.: American Mathematical Society. ss. 242-243. ISBN .
- ^ a b Gilbarg, David; (2001). Elliptic partial differential equations of second order. Berlin: Springer. ss. 149-150. ISBN .
- ^ John Hunter. "CHAPTER 3 Sobolev spaces (Lecture Notes on PDEs)" (PDF). www.math.ucdavis.edu. 22 Kasım 2024 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 3 Ocak 2025.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte zayif turev guclu turev olarak da bilinen olagan turev kavraminin bir genellemesidir Zayif turev kavrami turevlenebilir olmadigi ama bir Lebesgue uzayinda oldugu varsayilan fonksiyonlar icin gelistirilmis bir turev kavramidir Zayif turev kavrami ayni zamanda kavraminin tanimlanmasina da yol acar TanimTanimin arkasinda yatan ana fikir bir Lebesgue uzayi icindeki sonsuz turevli ve sahip fonksiyonlarin bu uzay icinde yogun olarak var olmasi gercegine dayanir Gercekten de turevlenebilir u displaystyle u ve f displaystyle varphi fonksiyonlari icin parcali integral yazilirsa abu x f x dx u x f x ab abu x f x dx displaystyle begin aligned int a b u x varphi x dx amp Big u x varphi x Big a b int a b u x varphi x dx 6pt end aligned elde edilir f displaystyle varphi fonksiyonu ayrica tikiz destege sahipse o zaman u x f x ab displaystyle Big u x varphi x Big a b terimi sifir olur Boylece turevli her u displaystyle u ve tikiz destege sahip sonsuz turevli her f displaystyle varphi fonksiyonu icin abu x f x dx abu x f x dx displaystyle begin aligned int a b u x varphi x dx amp int a b u x varphi x dx 6pt end aligned elde edilir Tikiz destege sahip sonsuz turevli f displaystyle varphi gibi fonksiyonlarin kumesi Lebesgue uzayinda yogun oldugundan u displaystyle u fonksiyonunun turevli oldugu varsayimi kaldirilarak asagidaki gibi basit bir zayif tanima ulasilabilir Basit tanim Gercel sayilar uzerindeki bir a b displaystyle a b uzerinde tanimli ve L1 a b displaystyle L 1 a b uzayinda yer alan bir u displaystyle u fonksiyonunu ele alalim f a f b 0 displaystyle varphi a varphi b 0 ozelligine sahip sonsuz turevli her f displaystyle varphi fonksiyonu icin abu t f t dt abv t f t dt displaystyle int a b u t varphi t dt int a b v t varphi t dt esitligini saglayan bir v displaystyle v in L1 a b displaystyle L 1 a b fonksiyonu varsa v displaystyle v fonksiyonuna u displaystyle u fonksiyonunun zayif turevi denir Genel tanim Oklid uzayindaki acik bir U Rn displaystyle U subset mathbb R n kumesinde tanimli ve gercel degerli fonksiyonlarin zayif turevini tanimlamak icin ilk once gosterimi altinda turev operatorunu tanimlayalim Nn a1 a2 an ai N i 1 n displaystyle mathbb N n alpha 1 alpha 2 ldots alpha n alpha i in mathbb N quad forall i 1 ldots n kumesi n textstyle n boyutlu dogal sayilar kumesi olsun x1 xn displaystyle x 1 cdots x n Oklid uzayindaki bagimsiz degiskenleri temsil etsin a a1 a2 an Nn displaystyle alpha alpha 1 alpha 2 cdots alpha n in mathbb N n icin a a1 a2 an displaystyle alpha alpha 1 alpha 2 cdots alpha n tanimlansin ve Da displaystyle D alpha turev operatorunu yeteri kadar turevli bir f displaystyle varphi icin Daf a f x1a1 xnan a1 x1a1 an xnanf displaystyle D alpha varphi frac partial alpha varphi partial x 1 alpha 1 cdots partial x n alpha n frac partial alpha 1 partial x 1 alpha 1 left cdots left frac partial alpha n partial x n alpha n varphi right right ile tanimlayalim Tanimin arkasinda yatan ana fikir yuksek boyutlu Oklid uzayinda da gecerlidir Diger deyisle a displaystyle alpha kere turevli her u U R displaystyle u U to mathbb R ve tikiz destege sahip sonsuz turevli her f displaystyle varphi fonksiyonu icin Uu Dafdx 1 a UDau fdx displaystyle begin aligned int U u D alpha varphi dx amp 1 alpha int U D alpha u varphi dx 6pt end aligned elde edilir bir u U R displaystyle u U to mathbb R fonksiyonunu yani U displaystyle U kumesindeki her uzerinde integrallenebilir bir u U R displaystyle u U to mathbb R fonksiyonunu ele alalim ve boyle bir fonksiyonu u Lloc1 U displaystyle u in L text loc 1 U ile gosterelim a a1 a2 an Nn displaystyle alpha alpha 1 alpha 2 cdots alpha n in mathbb N n olsun U displaystyle U uzerinde tikiz destege sahip sonsuz turevli her f displaystyle varphi fonksiyonu icin UuDaf 1 a Uvf displaystyle int U uD alpha varphi 1 alpha int U v varphi esitligini saglayan bir v Lloc1 U displaystyle v in L text loc 1 U fonksiyonu varsa o zaman v displaystyle v fonksiyonuna u displaystyle u fonksiyonunun a displaystyle alpha mertebesinden zayif turevi denir OzelliklerBir u displaystyle u fonksiyonunun zayif turevi varsa bu zayif turev Lebesgue anlaminda biriciktir Diger deyisle eger bir fonksiyonun iki zayif turevi varsa bu zayif turevler en fazla olcusu sifir olan kumeler uzerinde farkli degerler alirlar Bir baska deyimle bu ki fonksiyon birbirine esittir Fonksiyonlarin birbirine hemen hemen her yerde esit olan fonksiyonlarin denklik sinifi olarak alirsak o zaman turev biricik olacaktir Bu yuzden bir u displaystyle u fonksiyonunun zayif turevini Dau displaystyle D alpha u olarak gostermekte genelde sakinca yoktur Genellikle birden fazla zayif turevin varligi bir sorun degildir cunku fonksiyonlar hemen hemen her yerde esitse L p uzaylari ve teorisinde esdeger kabul edilir Guclu turevi Lebesgue uzayinda yer alan bir u displaystyle u fonksiyonu icin zayif turev tanimindaki integral kosulu zaten saglanacaktir Boylece zayif turev tanimi guclu turev tanimini genellestirmis olur Dahasi guclu turev icin gecerli olan toplamin turevi ya da carpimin turevi gibi kurallar zayif turevlilik icin de gecerli olacaktir Baska bir zayif turev ozelligi ise zayif turevi 0 olan bir fonksiyonun sabit olmasi gerektigidir Gercekten de bir a b displaystyle a b araligi uzerinde gercel degerler alan boyle bir f displaystyle f fonksiyonunun sabit oldugunu gostermek icin soyle tartisilabilir Ilk once zayif turev tanimi geregi sonsuz turevli ve tikiz destekli harhangi bir ϕ displaystyle phi fonksiyonu icin abfϕ dx 0 displaystyle int a b f phi dx 0 olacaktir h displaystyle eta fonksiyonu a b displaystyle a b araliginda tikiz destekli ve bu aralik uzerinde integrali 1e esit olan sonsuz turevli bir fonksiyon olsun O zaman sonsuz turevli ve tikiz destekli herhangi bir ϕ displaystyle phi fonksiyonu icin A abϕdx ve ps x ax ϕ t Ah t dt displaystyle A int a b phi dx quad text ve quad psi x int a x left phi t A eta t right dt yazarak ϕ Ah ps displaystyle phi A eta psi yazilabilir O zaman c abfhdx displaystyle c int a b f eta dx olmak uzere abfϕdx A abfhdx abfps dx A abfhdx c abϕ displaystyle int a b f phi dx A int a b f eta dx int a b f psi dx A int a b f eta dx c int a b phi olur Bu yuzden sonsuz turevli ve tikiz destekli harhangi bir ϕ displaystyle phi fonksiyonu icin ab f c ϕdx 0 displaystyle int a b f c phi dx 0 olur ki bu da noktasal olarak hemen hemen her yerde f c displaystyle f c esitligini verir Sonuc olarak f displaystyle f sabit bir fonksiyona denktir Ornekleru R R u t t displaystyle u mathbb R rightarrow mathbb R u t t olarak tanimlanan mutlak deger fonksiyonunun t 0 displaystyle t 0 noktasinda turevi yoktur Yine de isaret fonksiyonu olarak da bilinen v R R displaystyle v mathbb R rightarrow mathbb R v t 1t gt 0 ise 0t 0 ise 1t lt 0 ise displaystyle v t begin cases 1 amp t gt 0 text ise 6pt 0 amp t 0 text ise 6pt 1 amp t lt 0 text ise end cases fonksiyonu u displaystyle u nun zayif turevidir Daha once vurgu yapildigi uzere bu fonksiyondan sifir olculu herhangi bir gercel sayilar kumesinde farklilasan baska herhangi bir fonksiyon yine u displaystyle u nun zayif turevi olacaktir Ornegin yukaridaki isaret fonksiyon tanimindaki v 0 displaystyle v 0 tanimi herhangi bir sayi alinabilir Rasyonel sayilarin karakteristik fonksiyonu 1Q displaystyle 1 mathbb Q hicbir yerde turevli olmayan bir fonksiyondur ama bu fonksiyonun zayif turevi vardir Rasyonel sayilarin sifir oldugundan 1Q t f t dt 0 displaystyle int 1 mathbb Q t varphi t dt 0 olur Boylece v t 0 displaystyle v t 0 olarak tanimlanan sifir fonksiyonu 1Q displaystyle 1 mathbb Q fonksiyonunun zayif turevi olur Yalniz burada dikkat edilmesi gereken bu zayif turevin sezgilerimize ters olabilecegidir Diger deyisle 1Q displaystyle 1 mathbb Q bir Lp displaystyle L p uzayinin uyesi olarak dusunuldugunde sifir fonksiyonu ile ayni sahiptir yani bu fonksiyonlar sifir olan Q displaystyle mathbb Q kumesi uzerinde farklilasirlar Zayif turev kavrami turevliligi genellestirmez Diger deyisle hemen hemen her yerde turevi olan bir fonksiyonun zayif turevi olmayabilir Ornegin c displaystyle c sureklidir ve hemen hemen her yerde turevi de vardir Ancak bu fonksiyonun zayif turevi yoktur Fonksiyonun zayif turevi olsaydi o zaman bu zayif turevin Cantor fonksiyonunun sabit oldugu her aralikta 0 degeri almasi gerekirdi Gercekten de boyle bir aralikta destegi olmayan sonsuz turevli fonksiyonlar araciligiyla bu ozellik gosterilebilr Ama bu gibi araliklarin birlesiminin olcusu 1 olacagi icin o zaman bu zayif turevin hemen hemen her yerde 0 degeri almasi gerekirdi Ancak zayif turevi 0 olan bir fonksiyon aslinda hemen hemen her yerde sabit fonksiyondur Sonuc olarak Cantor fonksiyonu surekliliginden dolayi her yerde sabit fonksiyon olacaktir Boylece 0 c 0 lt c 1 1 displaystyle 0 c 0 lt c 1 1 olan bir fonksiyon icin sabit oldugu cikarimi yapildi ki bu da bir celiskidir Bu yuzden bastaki zayif turevin varligi varsayimi yanlistir Ayrica bakinizKaynakca a b c Evans Lawrence C 1998 Partial differential equations Providence R I American Mathematical Society ss 242 243 ISBN 0 8218 0772 2 a b Gilbarg David 2001 Elliptic partial differential equations of second order Berlin Springer ss 149 150 ISBN 3 540 41160 7 John Hunter CHAPTER 3 Sobolev spaces Lecture Notes on PDEs PDF www math ucdavis edu 22 Kasim 2024 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 3 Ocak 2025
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State








