Bu maddede bulunmasına karşın yetersizliği nedeniyle bazı bilgilerin hangi kaynaktan alındığı belirsizdir. (Şubat 2020) () |
Trilineer interpolasyon, 3-boyutlu bir grid üzerinde çok-değişkenli bir interpolasyon metodudur. Trilineer interpolasyon, sıklıkla, nümerik analiz, veri analizi ve bilgisayar grafiklerinde kullanılır.
Lineer ve bilineer interpolasyonlar ile kıyası
Trilineer interpolasyon, 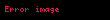
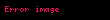
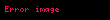
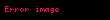
Birçok yöntemle, trilineer interpolasyon denklemini türetmek mümkündür. Trilineer interpolasyon, 3-boyutlu 1.seviye B-spline interpolasyon tensörüne denktir. Ayrıca, interpolasyon operatörü, 3 lineer interpolasyon operatörünün tensörel çarpımına eşittir.
Metot



Periyodik ve kübik bir latis üzerinde, 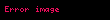

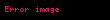







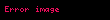
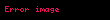
İlk olarak, 
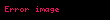


Son olarak, denklem 
Bu ifade, interpole edilen noktadaki fonksiyon değerini vermektedir.
Trilineer interpolasyonun sonucu, üç farklı eksende yapılan üç lineer interpolasyonun işlem sırasından bağımsızdır. Örneğin, işlem sırası 





Yukarıdaki işlemler şu şekilde de görselleştirilebilir: İlk önce, interpole edilecek noktayı kapsayan bir kübün sekiz köşe noktasının koordinatları bulunur. Bu köşe noktaları, varsayılsın ki, şu değerlere sahiptir: C000, C100, C010, C110, C001, C101, C011, C111.
Akabinde, C00'ı bulmak için C000 ve C100 ile lineer interpolasyon yapılır. Lineer interpolasyon, aynı şekilde, C01 için C001 ve C101 arasında; C11 için C011 ve C111 arasında; ve C10 için C010 ve C110 arasında uygulanır.
Ardından, C0 için C00 ve C10 arası; ve C1 için C01 ve C11 arası lineer interpolasyon uygulanır.
Son adımda, C değeri, C0 ve C1 arasında lineer interpolasyonla elde edilir.
Tüm bunlara ek olarak, trilineer interpolasyon, iki bilineer interpolasyon ve bir lineer interpolasyonun kombinasyonu ile de ulaşılabilir:
Ayrıca bakınız
Dış bağlantılar
- İnvers iteratif trilineer interpolasyon için NASA'nın yayımladığı bir kodsu10 Ekim 2006 tarihinde Wayback Machine sitesinde ..
- Paul Bourke, Interpolation methods26 Ağustos 2012 tarihinde Wayback Machine sitesinde ., 1999. Yayın, trilineer interpolasyon için ikili mantık sistemine dayanan basit ve etkili bir yöntem sunmaktadır. Ayrıca, metot, n-boyuta genişletilebilir (ör. tetralineer, pentalineer vb.).
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede kaynak listesi bulunmasina karsin metin ici kaynaklarin yetersizligi nedeniyle bazi bilgilerin hangi kaynaktan alindigi belirsizdir Lutfen kaynaklari uygun bicimde metin icine yerlestirerek maddenin gelistirilmesine yardimci olun Subat 2020 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Trilineer interpolasyon 3 boyutlu bir grid uzerinde cok degiskenli bir interpolasyon metodudur Trilineer interpolasyon siklikla numerik analiz veri analizi ve bilgisayar grafiklerinde kullanilir Lineer ve bilineer interpolasyonlar ile kiyasiTrilineer interpolasyon D 1 displaystyle D 1 boyuttaki lineer interpolasyon ve D 2 displaystyle D 2 boyuttaki bilineer interpolasyonun D 3 displaystyle D 3 boyutundaki uzantisidir Bu interpolasyon metotlarinin dogruluk seviyesi order of accuracy 1 dir Yani sira bu metot interpole edilecek noktanin cevresinden 1 n D 8 displaystyle 1 n D 8 nokta degerine ihtiyac duyar Bircok yontemle trilineer interpolasyon denklemini turetmek mumkundur Trilineer interpolasyon 3 boyutlu 1 seviye B spline interpolasyon tensorune denktir Ayrica interpolasyon operatoru 3 lineer interpolasyon operatorunun tensorel carpimina esittir MetotInterpolasyon noktasi C nin etrafinda kup uzeri sekiz kose noktasi3 boyutlu interpolasyon gosterimiTrilineer interpolasyonun geometrik gosterimi Elde edilmek istenen nokta ile butun hacmin carpimi her bir kose noktasindaki deger ile caprazindaki ufak hacmin carpimlarinin toplamina esittir Periyodik ve kubik bir latis uzerinde xd displaystyle x d yd displaystyle y d ve zd displaystyle z d nin x displaystyle x y displaystyle y z displaystyle z in her biri ile daha kucuk bir koordinatin arasindaki fark oldugunu dusunelim xd x x0 x1 x0 displaystyle x d x x 0 x 1 x 0 yd y y0 y1 y0 displaystyle y d y y 0 y 1 y 0 zd z z0 z1 z0 displaystyle z d z z 0 z 1 z 0 x0 displaystyle x 0 latis uzerinde x displaystyle x den kucuk bir nokta ve x1 displaystyle x 1 x displaystyle x den buyuk bir noktadir Ayni durum y0 y1 z0 displaystyle y 0 y 1 z 0 ve z1 displaystyle z 1 icin gecerlidir Ilk olarak x displaystyle x dogrultusunda interpolasyon yapilir kubun on yuzunun arka yuze dogru itildigini dusunun Sonucunda c00 V x0 y0 z0 1 xd V x1 y0 z0 xd displaystyle c 00 V x 0 y 0 z 0 1 x d V x 1 y 0 z 0 x d c01 V x0 y0 z1 1 xd V x1 y0 z1 xd displaystyle c 01 V x 0 y 0 z 1 1 x d V x 1 y 0 z 1 x d c10 V x0 y1 z0 1 xd V x1 y1 z0 xd displaystyle c 10 V x 0 y 1 z 0 1 x d V x 1 y 1 z 0 x d c11 V x0 y1 z1 1 xd V x1 y1 z1 xd displaystyle c 11 V x 0 y 1 z 1 1 x d V x 1 y 1 z 1 x d V x0 y0 z0 displaystyle V x 0 y 0 z 0 x0 y0 z0 displaystyle x 0 y 0 z 0 noktasindaki fonksiyon degeridir Ikinci olarak y displaystyle y dogrultusunda interpolasyon yapilir kubun ust kenarinin alt kenarina dogru itildigini dusunun Sonucta c0 c00 1 yd c10yd displaystyle c 0 c 00 1 y d c 10 y d c1 c01 1 yd c11yd displaystyle c 1 c 01 1 y d c 11 y d Son olarak denklem z displaystyle z dogrultusunda interpole edilir geride kalan cizgi boyunca ilerlendigini dusunun c c0 1 zd c1zd displaystyle c c 0 1 z d c 1 z d Bu ifade interpole edilen noktadaki fonksiyon degerini vermektedir Trilineer interpolasyonun sonucu uc farkli eksende yapilan uc lineer interpolasyonun islem sirasindan bagimsizdir Ornegin islem sirasi x displaystyle x y displaystyle y z displaystyle z olan bir trilineer interpolasyonunun sonucu islem sirasi y displaystyle y z displaystyle z x displaystyle x olan interpolasyon ile aynidir Yukaridaki islemler su sekilde de gorsellestirilebilir Ilk once interpole edilecek noktayi kapsayan bir kubun sekiz kose noktasinin koordinatlari bulunur Bu kose noktalari varsayilsin ki su degerlere sahiptir C000 C100 C010 C110 C001 C101 C011 C111 Akabinde C00 i bulmak icin C000 ve C100 ile lineer interpolasyon yapilir Lineer interpolasyon ayni sekilde C01 icin C001 ve C101 arasinda C11 icin C011 ve C111 arasinda ve C10 icin C010 ve C110 arasinda uygulanir Ardindan C0 icin C00 ve C10 arasi ve C1 icin C01 ve C11 arasi lineer interpolasyon uygulanir Son adimda C degeri C0 ve C1 arasinda lineer interpolasyonla elde edilir Tum bunlara ek olarak trilineer interpolasyon iki bilineer interpolasyon ve bir lineer interpolasyonun kombinasyonu ile de ulasilabilir C l b C000 C010 C100 C110 b C001 C011 C101 C111 displaystyle C approx l b C 000 C 010 C 100 C 110 b C 001 C 011 C 101 C 111 Ayrica bakinizLineer interpolasyon Bilineer interpolasyonDis baglantilarInvers iteratif trilineer interpolasyon icin NASA nin yayimladigi bir kodsu10 Ekim 2006 tarihinde Wayback Machine sitesinde Paul Bourke Interpolation methods26 Agustos 2012 tarihinde Wayback Machine sitesinde 1999 Yayin trilineer interpolasyon icin ikili mantik sistemine dayanan basit ve etkili bir yontem sunmaktadir Ayrica metot n boyuta genisletilebilir or tetralineer pentalineer vb
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State