Lineer cebirde bir matris, Gauss eliminasyonunun sonucu olan şekle sahipse eşelon biçimindedir.
Bir matrisin satır basamak formunda olması, satırlar üzerinde Gauss eliminasyonu işlemleri yapıldığı anlamına gelir. Sütun basamak formu ise Gauss eliminasyonunun sütunlar üzerinde yapılmış olduğu anlamına gelir. Başka bir deyişle, bir matrisin transpozu satır basamak biçiminde ise, matris sütun basamak biçimindedir. Bu nedenle bu makalenin geri kalanında yalnızca satır basamaklı formlar ele alınacaktır. Sütun basamak formunun benzer özellikleri, tüm matrislerin yer değiştirmesi ile kolayca çıkarılabilir. Bir matris bu özellikleri taşıyorsa satır basamak formundadır.
- Yalnızca sıfırlardan oluşan tüm satırlar en alttadır.
- Sıfırdan farklı her satırın baştaki değeri (sıfırdan sonra gelen en soldaki değer), yukarıdaki satırın baştaki değerinin sağındadır.
Bazı metinler baş katsayının 1 olması şartını da ekler, bazıları ise katsayıların 1 olduğu örnekleri indirgenmiş satır basamaklı form olarak kabul eder.
Bu iki koşul, bir sütundaki baş katsayının altındaki tüm değerlerin sıfır olduğu anlamına gelir.
Aşağıdaki, satır basamak formundaki 4x5'lik bir matris örneğidir, bu matris indirgenmiş satır basamak formunda değildir (aşağıya bakınız):
Matrislerin kerte ve boşuzay gibi pek çok özelliği, satır basamak formlarından kolayca çıkarılabilir.
İndirgenmiş satır basamak formu
| ]Bir matris, aşağıdaki koşulları karşılıyorsa indirgenmiş satır basamaklı formdadır (aynı zamanda satır kanonik formu da denir):
- Sıralı basamak formundadır.
- Sıfırdan farklı her satırın başındaki değer 1'dir.
- Başında 1 bulunan her sütunun diğer tüm değerleri sıfırdır.
Bir matrisin indirgenmiş sıralı basamak formu Gauss-Jordan eliminasyonu ile hesaplanabilir. Satır basamaklı formundan farklı olarak, bir matrisin indirgenmiş satırlı basamaklı biçimi benzersizdir ve hesaplamak için kullanılan algoritmaya bağlı değildir. Belirli bir matris için, satır basamak formu benzersiz olmamasına rağmen, tüm satır basamak ve indirgenmiş satır basamak formları aynı sayıda sıfır satıra sahiptir ve pivotlar aynı indekslerde yer almaktadır.
Aşağıdaki, indirgenmiş satır basamak basamak formundaki bir matris örneğidir. Görüldüğü üzere, matrisin sol kısmı her zaman birim matris olmayabilir.
Tamsayı katsayılı matrisler için Hermite normal formu, kalanlı bölme kullanılarak ve herhangi bir rasyonel sayı veya payda kullanılmadan hesaplanabilen bir satır basamak formudur. Öte yandan, tam sayı katsayılı bir matrisin indirgenmiş basamak formu genellikle tam sayı olmayan katsayılar içerir.
Satır kademe formuna dönüşüm
| ]Gauss eliminasyonu adı verilen sonlu temel satır işlemleri dizisi aracılığıyla, herhangi bir matris satır basamak formuna dönüştürülebilir. Temel satır işlemleri matrisin koruduğu için, satır basamak basamak formunun satır uzayı orijinal matrisin satır uzayıyla aynıdır.
Ortaya çıkan kademeli form benzersiz değildir; basamak formundaki herhangi bir matris, yukarıdaki satırlardan birine bir satırın skaler katının eklenmesiyle (eşdeğer) basamak formuna yerleştirilebilir, örneğin:
Bununla birlikte, her matrisin benzersiz bir indirgenmiş sıralı basamak formu vardır. Yukarıdaki örnekte indirgenmiş sıralı basamak formu şu şekilde bulunabilir:
Bu, indirgenmiş satırlı basamak formunun sıfırdan farklı satırlarının, orijinal matrisin satır uzayı için benzersiz indirgenmiş satır basamaklı oluşturma kümesi olduğu anlamına gelir.
Kaynakça
| ]- ^ Phrased in terms of each individual zero row in Leon (2010):"A matrix is said to be in row echelon form ... (iii) If there are rows whose entries are all zero, they are below the rows having nonzero entries."
- ^ Leon (2010):"A matrix is said to be in row echelon form ... (ii) If row k does not consist entirely of zeros, the number of leading zero entries in row is greater than the number of leading zero entries in row k."
- ^ See, for instance, the first clause of the definition of row echelon form in Leon (2010): "A matrix is said to be in row echelon form (i) If the first nonzero entry in each nonzero row is 1."
- ^ a b Meyer 2000
- ^ a b Howard Anton, Chris Rorres (23 Ekim 2013). Elementary Linear Algebra: Applications Version, 11th Edition (İngilizce). Wiley Global Education. s. 21. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Vikipedi ozgur ansiklopedi Lineer cebirde bir matris Gauss eliminasyonunun sonucu olan sekle sahipse eselon bicimindedir Bir matrisin satir basamak formunda olmasi satirlar uzerinde Gauss eliminasyonu islemleri yapildigi anlamina gelir Sutun basamak formu ise Gauss eliminasyonunun sutunlar uzerinde yapilmis oldugu anlamina gelir Baska bir deyisle bir matrisin transpozu satir basamak biciminde ise matris sutun basamak bicimindedir Bu nedenle bu makalenin geri kalaninda yalnizca satir basamakli formlar ele alinacaktir Sutun basamak formunun benzer ozellikleri tum matrislerin yer degistirmesi ile kolayca cikarilabilir Bir matris bu ozellikleri tasiyorsa satir basamak formundadir Yalnizca sifirlardan olusan tum satirlar en alttadir Sifirdan farkli her satirin bastaki degeri sifirdan sonra gelen en soldaki deger yukaridaki satirin bastaki degerinin sagindadir Bazi metinler bas katsayinin 1 olmasi sartini da ekler bazilari ise katsayilarin 1 oldugu ornekleri indirgenmis satir basamakli form olarak kabul eder Bu iki kosul bir sutundaki bas katsayinin altindaki tum degerlerin sifir oldugu anlamina gelir Asagidaki satir basamak formundaki 4x5 lik bir matris ornegidir bu matris indirgenmis satir basamak formunda degildir asagiya bakiniz 1a0a1a2a3002a4a50001a600000 displaystyle left begin array ccccc 1 amp a 0 amp a 1 amp a 2 amp a 3 0 amp 0 amp 2 amp a 4 amp a 5 0 amp 0 amp 0 amp 1 amp a 6 0 amp 0 amp 0 amp 0 amp 0 end array right Matrislerin kerte ve bosuzay gibi pek cok ozelligi satir basamak formlarindan kolayca cikarilabilir Indirgenmis satir basamak formu span Bir matris asagidaki kosullari karsiliyorsa indirgenmis satir basamakli formdadir ayni zamanda satir kanonik formu da denir Sirali basamak formundadir Sifirdan farkli her satirin basindaki deger 1 dir Basinda 1 bulunan her sutunun diger tum degerleri sifirdir Bir matrisin indirgenmis sirali basamak formu Gauss Jordan eliminasyonu ile hesaplanabilir Satir basamakli formundan farkli olarak bir matrisin indirgenmis satirli basamakli bicimi benzersizdir ve hesaplamak icin kullanilan algoritmaya bagli degildir Belirli bir matris icin satir basamak formu benzersiz olmamasina ragmen tum satir basamak ve indirgenmis satir basamak formlari ayni sayida sifir satira sahiptir ve pivotlar ayni indekslerde yer almaktadir Asagidaki indirgenmis satir basamak basamak formundaki bir matris ornegidir Goruldugu uzere matrisin sol kismi her zaman birim matris olmayabilir 10a10b101a20b20001b3 displaystyle left begin array ccccc 1 amp 0 amp a 1 amp 0 amp b 1 0 amp 1 amp a 2 amp 0 amp b 2 0 amp 0 amp 0 amp 1 amp b 3 end array right Tamsayi katsayili matrisler icin Hermite normal formu kalanli bolme kullanilarak ve herhangi bir rasyonel sayi veya payda kullanilmadan hesaplanabilen bir satir basamak formudur Ote yandan tam sayi katsayili bir matrisin indirgenmis basamak formu genellikle tam sayi olmayan katsayilar icerir Satir kademe formuna donusum span Gauss eliminasyonu adi verilen sonlu temel satir islemleri dizisi araciligiyla herhangi bir matris satir basamak formuna donusturulebilir Temel satir islemleri matrisin korudugu icin satir basamak basamak formunun satir uzayi orijinal matrisin satir uzayiyla aynidir Ortaya cikan kademeli form benzersiz degildir basamak formundaki herhangi bir matris yukaridaki satirlardan birine bir satirin skaler katinin eklenmesiyle esdeger basamak formuna yerlestirilebilir ornegin 13 1017 2 satiri 1 satira ekleme 146017 displaystyle begin bmatrix 1 amp 3 amp 1 0 amp 1 amp 7 end bmatrix xrightarrow text 2 satiri 1 satira ekleme begin bmatrix 1 amp 4 amp 6 0 amp 1 amp 7 end bmatrix Bununla birlikte her matrisin benzersiz bir indirgenmis sirali basamak formu vardir Yukaridaki ornekte indirgenmis sirali basamak formu su sekilde bulunabilir 13 1017 2 satiri 3 ile carparak 1 satirdan cikar 10 22017 displaystyle begin bmatrix 1 amp 3 amp 1 0 amp 1 amp 7 end bmatrix xrightarrow text 2 satiri 3 ile carparak 1 satirdan cikar begin bmatrix 1 amp 0 amp 22 0 amp 1 amp 7 end bmatrix Bu indirgenmis satirli basamak formunun sifirdan farkli satirlarinin orijinal matrisin satir uzayi icin benzersiz indirgenmis satir basamakli olusturma kumesi oldugu anlamina gelir Kaynakca span Phrased in terms of each individual zero row in Leon 2010 A matrix is said to be in row echelon form iii If there are rows whose entries are all zero they are below the rows having nonzero entries Leon 2010 A matrix is said to be in row echelon form ii If row k does not consist entirely of zeros the number of leading zero entries in row k 1 displaystyle k 1 is greater than the number of leading zero entries in row k See for instance the first clause of the definition of row echelon form in Leon 2010 A matrix is said to be in row echelon form i If the first nonzero entry in each nonzero row is 1 a b Meyer 2000 a b Howard Anton Chris Rorres 23 Ekim 2013 Elementary Linear Algebra Applications Version 11th Edition Ingilizce Wiley Global Education s 21 ISBN 9781118879160 Kategoriler Sayisal dogrusal cebirLineer cebirLineer cebir teoremleri
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
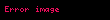
![{\displaystyle \left[{\begin{array}{ccccc}1&0&a_{1}&0&b_{1}\\0&1&a_{2}&0&b_{2}\\0&0&0&1&b_{3}\end{array}}\right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4d1kySmxNbUV5TmpjeE1tUXpaVE0zTnpnM1pEUTJZakE0TjJVNU56YzBPRGMwTUdJMU5UTmwuc3Zn.svg)