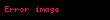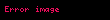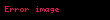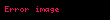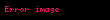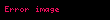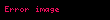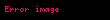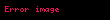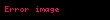Doğrusal cebirde, bir birim matrisde yalnızca bir tane elementer satır işlem yapılarak elde edilen matrislere elementer matris denir. m boyutunda bir birim matrisin üzerinde e elementer satır işlemi yapılarak elde edilen elementer matris şeklinde gösterilir.
Elementer Satır İşlemleri
Üç çeşit elementer satır işlemi vardır:
- Yer değiştirme
- Matrisin iki satırdaki tüm elemanların yerlerini değiştirilmesi.
- Çarpma
- Matrisdeki bir satırın her elemanın, sıfır dışında bir katsayı ile çarpılması.
- Toplama
- Matrisdeki satırlardan birinin, bir katının diğer bir satıra eklenmesi.
Elementer Matrislerin Tersi
Her elementer matris tersinirdir ve
yani 
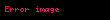

- Yer değiştirmenin tersi
ise
- Yani yer değiştirme işleminin tersi kendisine eşittir çünkü
ve
satırlarının yerini değiştirmek ile
ve
satırlarının yerini değiştirmek aynı şeye denk gelmektedir. Bundan dolayı da yer değiştirme işlemi uygulanarak elde edilen elementer matrislerin tersi kendilerine eşittir.
- Çarpmanın tersi
ise
- Toplamanın tersi
ise
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Dogrusal cebirde bir birim matrisde yalnizca bir tane elementer satir islem yapilarak elde edilen matrislere elementer matris denir m boyutunda bir birim matrisin uzerinde e elementer satir islemi yapilarak elde edilen elementer matris e Im displaystyle e I m seklinde gosterilir Elementer Satir IslemleriUc cesit elementer satir islemi vardir Yer degistirme Matrisin iki satirdaki tum elemanlarin yerlerini degistirilmesi Ri Rj displaystyle R i leftrightarrow R j Carpma Matrisdeki bir satirin her elemanin sifir disinda bir katsayi ile carpilmasi kRi Ri k 0 iken displaystyle kR i rightarrow R i k neq 0 mbox iken Toplama Matrisdeki satirlardan birinin bir katinin diger bir satira eklenmesi Ri kRj Ri i j iken displaystyle R i kR j rightarrow R i i neq j mbox iken Elementer Matrislerin TersiHer elementer matris tersinirdir ve e Im 1 e 1 Im displaystyle e I m 1 e 1 I m yani e Im displaystyle e I m elementer matrisinin tersini almak yerine Im displaystyle I m birim matrisi uzerinde e displaystyle e elementer islemini tersi uygulanabilir Elementer islemlerin tersi soyle tanimlanmistir Yer degistirmenin tersi e Ri Rj displaystyle e R i leftrightarrow R j ise e 1 Rj Ri displaystyle e 1 R j leftrightarrow R i Yani yer degistirme isleminin tersi kendisine esittir cunku Ri displaystyle R i ve Rj displaystyle R j satirlarinin yerini degistirmek ile Rj displaystyle R j ve Ri displaystyle R i satirlarinin yerini degistirmek ayni seye denk gelmektedir Bundan dolayi da yer degistirme islemi uygulanarak elde edilen elementer matrislerin tersi kendilerine esittir Carpmanin tersi e kRi Ri k 0 iken displaystyle e kR i rightarrow R i k neq 0 mbox iken ise e 1 1kRi Ri k 0 iken displaystyle e 1 frac 1 k R i rightarrow R i k neq 0 mbox iken Toplamanin tersi e Ri kRj Ri i j iken displaystyle e R i kR j rightarrow R i i neq j mbox iken ise e 1 Ri k Rj Ri i j iken displaystyle e 1 R i k R j rightarrow R i i neq j mbox iken Kaynakca
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State