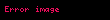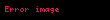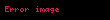Matematikte, bir karmaşık sayısının sanal kısmı, 'yi temsil eden gerçel sayıların ikinci elemandır; yani ise veya denk bir şekilde ise, o zaman 'nin sanal kısmı 'dir. İngilizce karşılığından esinlenerek, Im{z} ile veya Fraktür yazıtipindeki büyük I kullanılarak, yani {z} ile gösterilir. 'yi, 'nin sanal kısmına gönderen holomorf değildir.


kullanıldığında, 'nin gerçel kısmı ifadesine eşit olur.
Kutupsal biçim deki bir karmaşık sayısı için, kartezyen (dikdörtgensel)koordinatlar veya dengi bir ifadeyle 'dır. Euler formülünden olduğu ve bu yüzden 'ın sanal kısmının olduğu ortaya çıkar.
Elektrik gücünde, sinüs dalgası voltajı bir "doğrusal" yük (başka bir deyişle, akımı da bir sinüs dalgası yapan yük) taşıdığında, güç tellerindeki akımı ile temsil edilir (mühendisler aynı zamanda elektrik akımını da simgeleyen yerine sanal birim olarak harfini kullanırlar). "Gerçel akım" , voltaj maksimum olduğundaki akım ile ilişkindir. Gerçel akım ile voltajın çarpımı yük tarafından tüketilen esas gücü verir (genelde çoğu güç ısı olarak harcanır). "Sanal akım" ise voltaj sıfır olduğundaki akım ile ilişkindir. Tamamen sanal akıma sahip (kapasitör veya indüktör gibi) bir yük hiç güç harcamaz, sadece gücü geçici bir şekilde kabul eder ve daha sonra gücü güç tellerine iter.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir z displaystyle z karmasik sayisinin sanal kismi z displaystyle z yi temsil eden gercel sayilarin ikinci elemandir yani z x y displaystyle z x y ise veya denk bir sekilde z x iy displaystyle z x iy ise o zaman z displaystyle z nin sanal kismi y displaystyle y dir Ingilizce karsiligindan esinlenerek Im z ile veya Fraktur yazitipindeki buyuk I kullanilarak yani ℑ displaystyle Im z ile gosterilir z displaystyle z yi z displaystyle z nin sanal kismina gonderen holomorf degildir I semboluKarmasik duzlemin bir gosterimi z x iy displaystyle z x iy karmasik sayisinin gercel kismi y displaystyle y dir z displaystyle bar z kullanildiginda z displaystyle z nin gercel kismi z z 2i displaystyle frac z bar z 2i ifadesine esit olur Kutupsal bicim deki bir karmasik z r 8 displaystyle z r theta sayisi icin kartezyen dikdortgensel koordinatlar z rcos 8 rsin 8 displaystyle z r cos theta r sin theta veya dengi bir ifadeyle z r cos 8 isin 8 displaystyle z r cos theta i sin theta dir Euler formulunden z rei8 displaystyle z re i theta oldugu ve bu yuzden rei8 displaystyle re i theta in sanal kisminin rsin 8 displaystyle r sin theta oldugu ortaya cikar Elektrik gucunde sinus dalgasi voltaji bir dogrusal yuk baska bir deyisle akimi da bir sinus dalgasi yapan yuk tasidiginda guc tellerindeki I displaystyle I akimi I x jy displaystyle I x jy ile temsil edilir muhendisler ayni zamanda elektrik akimini da simgeleyen i displaystyle i yerine sanal birim olarak j displaystyle j harfini kullanirlar Gercel akim x displaystyle x voltaj maksimum oldugundaki akim ile iliskindir Gercel akim ile voltajin carpimi yuk tarafindan tuketilen esas gucu verir genelde cogu guc isi olarak harcanir Sanal akim y displaystyle y ise voltaj sifir oldugundaki akim ile iliskindir Tamamen sanal akima sahip kapasitor veya induktor gibi bir yuk hic guc harcamaz sadece gucu gecici bir sekilde kabul eder ve daha sonra gucu guc tellerine iter Ayrica bakinizGercel kisim
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State