Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:
Karmaşık sayılar kümesi C şeklinde gösterilir. . özelliğini sağlayan sanal birime denir. Kimi zaman özellikle elektrik mühendisliğinde yerine, kullanılır.
Ayrıca matematikte bu sayıların uzayı olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizcede karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.
Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Diğer bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar.
Bir z karmaşık sayısının gerçel ve sanal parçaları sırasıyla Re(z) ve Im(z) fonksiyonlarıyla gösterilir. Bütün bu tanımları ve özellikleri bir örnekte gösterelim. sayısı gerçel kısmı Re(4-7i)=4, sanal kısmı Im(4-7i)=-7 olan uzayında bir karmaşık sayıdır.Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.
Tanım
Karmaşık sayılar kümesi birçok şekilde tanımlanabilir. Aşağıdaki tanımların hepsi birbirine , yani yapısal olarak biri diğerinin yerine kullanılabilir. Bu yüzden aslında içerik olarak farklı olan aşağıda tanımlanan tüm kümeleri aynı harfle gösterdik, 
Kartezyen uzay tanımı
Gerçek sayılar kümesinde her sayıyı 

olarak tanımlanmış olur. Bu 2 boyutlu kartezyen uzay, Argand düzlemi olarak anılır. Eğer 

Karmaşık sayılar, bu tanımla aşağıdaki gibi ifade edilir: 
Burada açıkça 

Cisim genişlemesi tanımı
Karmaşık olmayan sayılar, gerçel sayılar cisminin bir . 


Bu durumda
olarak tanımlanır. Daha açık olarak, karmaşık sayılar gerçel sayılar polinom halkasının 
Bu bölüm halkasında X öğesinin görüntüsü 
Karmaşık düzlem

 (veya
(veya  olarak da gösterilir) dikdörtgendir ve noktayı ifade eder.
olarak da gösterilir) dikdörtgendir ve noktayı ifade eder.Karmaşık sayı, iki boyutlu kartezyen koordinat sisteminde, nokta veya konum vektörü olarak gösterilebilir. Sayılar alışıla geldiği gibi yatay bileşen gerçel kısmı ve düşey (dikey) bileşende sanal kısmı olarak çizildi (Şekil 1'e bakınız). Bu iki kısım karmaşık bir sayıyı ifade etmek için kullanılır ve bu yüzden Kartezyen-, dikdörtgensel- veya cebirsel form olarak adlandırılır.
İşlemlerin geometriksel açıklaması
Cebirsel olarak ifade edilen işlemler yukarıdaki karmaşık düzlem kullanılarak gösterilebilir.
 | X = A + B: Karmaşık düzlemdeki A ve B gibi iki noktanın 'toplamı, X = A + Bdir ve köşeleri 0,A, B olan bir üçgendir. X, B, A ile benzerdir. Bu iki karmaşık sayı, vektör uzayında aynı katkıya sahiptir. |
 | X = AB: A ve B gibi iki noktanın çarpımı X = ABdir ve köşeleri 0, 1, A olan bir üçgendir. 0, B, X benzer üçgenlerdir. |
 | X = A*: A noktasının , X = A*dır ve köşeleri 0, 1, Adır. 0, 1, Xnin . |
Bu geometrik açıklamalar, cebirsek problemlerin geometriksel biçime dönüştürmeyi sağlar. Ve tam tersi de geçerlidir (geometriksel problemler, cebirsel olarak çözülebilir). Örneğin, geometriksel şekil olan onyedigen problemi, Gauss tarafından şu şekilde cebirsel denklem analizine dönüştürüldü:x17 = 1 (Çokgene bakınız).


fonksiyonunun alan renklendirme çizimi. Ton, fonksiyon değişkenini ifade ederken, doygunluk ve miktarı ifade eder.
Kutupsal form

 veya
veya  .
.Diyagramlar çeşitli özellik gösteriler. Öncelikle Şekil 2'de r ile gösterilen orjin (merkez)den z noktasına olan uzaklık, mutlak değer olarak bilinir. Mutlak değer veya büyüklük 
Karmaşık sayılar arasındaki uzaklık genellikle, 

İkinci olarak, 

veya
(
olduğunda π ekleyerek,
olur).
φ değeri, 2π'nin herhangi çarpanı olarak değiştirilebilir ve yine aynı açıyı verir (burada radyan kullanıldığına dikkat ediniz). Bundan dolayı, arg fonksiyonu bazen çok değerli olarak ifade edilir, Fakat çoğunlukla değer 
Karmaşık sayıların çeşitli formlarda gösterilebilir. Kutupsal form, bir düzlemdeki noktanın tam konumunu belirten mutlak değer ve argüman bileşenleri olarak gösterilebilir, şöyle ki; (r,φ) kutupsal çiftlerinden, özgün dikdörtgenin koordinatları olan 
buna trigonometrik form denir ve bazen r cis φ olarak kısaltılır. Euler formülü kullanılarak şu şekilde gösterilebilir:
buna da üstel form denir. Elektrik Mühendisliği'nde daha çok açısal gösterim kullanımı yaygındır. Bu gösterim, A genlikli ve θ fazına sahip fazörü ifade eder ve şu şekilde yazılır:
Açısal gösterimde θ, hem radyan hem de derece olabilir. Elektrik akımını ifade eden i ile karıştırmamak için, Elektrik Mühendisliği'nde i yerine daha çok j kullanılır.
Kutupsal formdaki işlemler
Çarpma ve bölme kutupsal formda temel formüllere sahiptir:
ve
Bu formda her iki çarpanın (eşitliklerin solundakiler) katsayıları çarpımın özelliğinden dolayı yan yana (çarpma işleminde) veya alt alta (bölme işleminde) getirilebilirler. Diğer yandan üslü sayıların kuralları gereği ifadeler aynı ise (burada 
Üs tam sayı ise şöyle gösterilir:
Sonuç olarak kutupsal formlar kökleri bulmak içinde kullanılabilir. z herhangi karmaşık sayı olmak üzere ve n pozitif tam sayı için zn = c olarak gösterilebilir. Bu da cnin n. kökü diye okunur. Eğer c sıfır değilse, tam n tane farklı c nin kökü vardır (cebirin temel teoremine göre). r > 0 için, c = re iφ'de c nin n. kökleri:
Burada 
Karmaşık sayılarda işlem
Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir. Öncelikle iki karmaşık sayının eşitliğini verelim.
Eşitlik
Bir 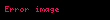

ancak
ve
iken geçerlidir.bu doğru bir kavramdır...
Toplama
Bir 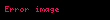

Çarpma
Bir 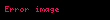

Eşlenik

Bir 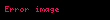

ya da matrislerde
olarak tanımlanır.
Eşleniğin cebirsel özellikleri
ancak z gerçel sayı olduğunda geçerlidir.
Çarpımsal ters
Bir 
olarak ya da bir uygun olarak
olduğu görülür.
Karmaşık sayının karekökü

burada 
Karmaşık sayının n dereceden kökü
Kök derecesi iki den büyük olan karmaşık sayıların genel denklemi uzundur. n sayısı artıkça genel denklemde uzar. Trigonometrik ve üstel biçim daha uygundur.
Üstel biçim :

Trigonometrik biçim :

Ayrıca bakınız
- Karmaşık analiz
- Hiperbolik sayılar
- Çifte karmaşık sayılar (bicomplex numbers)
- (Quaternions)
- (Octonions)
|
Başvuru ve Kaynaklar
- Notlar
- Kaynakça
- A. Mostowski & M. Stark, Introduction to Higher Algebra. Pergamon Press. New York: 1964.
- . Matematik Dünyası Dergisi. s. 64-73. 8 Ağustos 2020 tarihinde kaynağından arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte karmasik sayi bir gercel bir de sanal kisimdan olusan bir nesnedir a ve b sayilari gercek olursa karmasik sayilar su bicimde gosterilirler z a ib displaystyle z a mathbf i b Karmasik sayilar kumesi C seklinde gosterilir i2 1 displaystyle mathbf i 2 1 ozelligini saglayan sanal birime i displaystyle mathbf i denir Kimi zaman ozellikle elektrik muhendisliginde i displaystyle mathbf i yerine j displaystyle mathbf j kullanilir Ayrica matematikte bu sayilarin uzayi C displaystyle scriptstyle mathbb C olarak gosterilir Bu harfin secilmesinin nedeni Ingilizcede karmasik sozcugunun karsiligi olarak complex sozcugunun kullanilmasidir nitekim bazi Turkce kaynaklarda complex sozcugunden devsirilen kompleks sozcugune de raslanabilir Karmasik sayilara boyle bir adin verilmesinin nedeni ise asagida da gorecegimiz gibi gercel ve sanal kisimlarin bir arada durmasidir Butun gercel sayilar sanal kisimlari sifira esit olan birer karmasik sayi olarak dusunulebilir Diger bir deyisle gercel sayilar karmasik sayi duzleminde gercel sayilar ekseni uzerinde bulunurlar z a i 0 R displaystyle z a mathbf i cdot 0 in scriptstyle mathbb R Bir z karmasik sayisinin gercel ve sanal parcalari sirasiyla Re z ve Im z fonksiyonlariyla gosterilir Butun bu tanimlari ve ozellikleri bir ornekte gosterelim z 4 7i displaystyle z 4 7 mathbf i sayisi gercel kismi Re 4 7i 4 sanal kismi Im 4 7i 7 olan C displaystyle scriptstyle mathbb C uzayinda bir karmasik sayidir Bunun disinda karmasik sayilarin baska ozellikleri de vardir Ornegin bir karmasik sayi duzlemde bir vektor olarak temsil edilebilir TanimKarmasik sayilar kumesi bircok sekilde tanimlanabilir Asagidaki tanimlarin hepsi birbirine yani yapisal olarak biri digerinin yerine kullanilabilir Bu yuzden aslinda icerik olarak farkli olan asagida tanimlanan tum kumeleri ayni harfle gosterdik C displaystyle scriptstyle mathbb C Ayrica bu simge sadece karmasik sayilar dedigimiz ogeleri iceren bir kume olmaktan otedir uzerine tanimlayacagimiz iki tane ikili islemi olan bir cisimdir Ustelik bu cisim gercel sayilarin en buyuk cisim genislemesidir yani gercel sayilari bundan daha fazla genisletemeyiz Gercel sayilarla karmasik sayilarin ayni sahip oldugunu da unutmayalim Kartezyen uzay tanimi Gercek sayilar kumesinde her sayiyi i displaystyle mathbf i ile carparsak elde ettigimiz iR displaystyle mathbf i scriptstyle mathbb R kumesi onceki R displaystyle scriptstyle mathbb R kumesine esyapisaldir Karmasik sayilar cismi ise buradan hareketle C R iR a b a Rveb iR displaystyle scriptstyle mathbb C equiv scriptstyle mathbb R times mathbf i scriptstyle mathbb R equiv a b a in scriptstyle mathbb R text ve b in mathbf i scriptstyle mathbb R olarak tanimlanmis olur Bu 2 boyutlu kartezyen uzay Argand duzlemi olarak anilir Eger R displaystyle scriptstyle mathbb R yerine tam sayilar cismi Z displaystyle scriptstyle mathbb Z alinirsa olusan karmasik tam sayilar Bu sayilara da denir Karmasik sayilar bu tanimla asagidaki gibi ifade edilir z C displaystyle z in scriptstyle mathbb C olmak uzere z a b displaystyle z a b Burada acikca Re z a displaystyle Re z a ve Im z b displaystyle Im z b dir Cisim genislemesi tanimi Karmasik olmayan sayilar gercel sayilar cisminin bir i displaystyle mathbf i sayisi x2 1 displaystyle x 2 1 polinomunun koklerinden biridir ve diger koku de i displaystyle mathbf i olur Bu iki ogenin gercel sayilarla olan genislemesinin esyapisal oldugu kolaylikla gorulebilir R i R i displaystyle scriptstyle mathbb R left mathbf i right equiv scriptstyle mathbb R left mathbf i right Bu durumda C R i displaystyle scriptstyle mathbb C equiv scriptstyle mathbb R left mathbf i right olarak tanimlanir Daha acik olarak karmasik sayilar gercel sayilar polinom halkasinin x2 1 displaystyle x 2 1 polinomuyla uretilen bolum halkasidir C R X X2 1 a ib a b R displaystyle scriptstyle mathbb C equiv scriptstyle mathbb R X X 2 1 equiv a mathbf i b a b in scriptstyle mathbb R Bu bolum halkasinda X ogesinin goruntusu i displaystyle mathbf i karmasik birimidir Bu sayede karmasik sayilar halkasi olur ki bu gercel sayilarin cebirsel kapanisidir Cebirin temel teoremi bunu gerektirir n dereceli her polinomun tam n koku vardir Biz her karmasik sayinin a ib displaystyle a mathbf i b olarak ifade edildigi bu tanima daha asinayiz Karmasik duzlemSekil 1 Karmasik bir duzlemde nokta kirmizi ve konum vektoru mavi ile cizilen karmasik sayi a ib displaystyle a ib veya a bi displaystyle a bi olarak da gosterilir dikdortgendir ve noktayi ifade eder Karmasik sayi iki boyutlu kartezyen koordinat sisteminde nokta veya konum vektoru olarak gosterilebilir Sayilar alisila geldigi gibi yatay bilesen gercel kismi ve dusey dikey bilesende sanal kismi olarak cizildi Sekil 1 e bakiniz Bu iki kisim karmasik bir sayiyi ifade etmek icin kullanilir ve bu yuzden Kartezyen dikdortgensel veya cebirsel form olarak adlandirilir Islemlerin geometriksel aciklamasi Cebirsel olarak ifade edilen islemler yukaridaki karmasik duzlem kullanilarak gosterilebilir X A B Karmasik duzlemdeki A ve B gibi iki noktanin toplami X A Bdir ve koseleri 0 A B olan bir ucgendir X B A ile benzerdir Bu iki karmasik sayi vektor uzayinda ayni katkiya sahiptir X AB A ve B gibi iki noktanin carpimi X ABdir ve koseleri 0 1 A olan bir ucgendir 0 B X benzer ucgenlerdir X A A noktasinin X A dir ve koseleri 0 1 Adir 0 1 Xnin Bu geometrik aciklamalar cebirsek problemlerin geometriksel bicime donusturmeyi saglar Ve tam tersi de gecerlidir geometriksel problemler cebirsel olarak cozulebilir Ornegin geometriksel sekil olan onyedigen problemi Gauss tarafindan su sekilde cebirsel denklem analizine donusturuldu x17 1 Cokgene bakiniz f x x2 1 x 2 i 2x2 2 2i displaystyle f x tfrac x 2 1 x 2 i 2 x 2 2 2i fonksiyonunun alan renklendirme cizimi Ton fonksiyon degiskenini ifade ederken doygunluk ve miktari ifade eder Kutupsal form Sekil 2 f degiskeni ve r mutlak degeri karmasik duzlemdeki bir noktanin konumudur Noktanin kutupsal ifadesi soyledir r cos ϕ isin ϕ displaystyle r cos phi i sin phi veya reiϕ displaystyle re i phi Diyagramlar cesitli ozellik gosteriler Oncelikle Sekil 2 de r ile gosterilen orjin merkez den z noktasina olan uzaklik mutlak deger olarak bilinir Mutlak deger veya buyukluk z displaystyle z olarak yazilir Pisagor teoremine gore x iy x2 y2 displaystyle x iy sqrt x 2 y 2 Karmasik sayilar arasindaki uzaklik genellikle d z w z w displaystyle d z w z w fonksiyonu ile gosterilir Bu fonksiyon karmasik sayilarin metrik uzayina donusudur Limit ve sureklilik hakkinda fikir verir Iki boyutlu uzayin tum standart ozellikleri karmasik sayilar icin gecerlidir tum z ve w icin z w z w displaystyle z w leq z w Ikinci olarak z x iy displaystyle z x iy seklindeki karmasik sayinin argumani veya fazi reel eksenle yaptigi acidir Sekil 2 de f olarak gosteriliyor ve arg z displaystyle arg z olarak yazilir Mutlak deger olarak arguman dikdortgensel formdan elde edilebilir x iy displaystyle x iy f arctan yx displaystyle varphi arctan frac y x veya f p arctan yx displaystyle varphi pi arctan frac y x x lt 0 displaystyle x lt 0 oldugunda p ekleyerek x iy r cos ϕ isin ϕ displaystyle x iy r cos phi i sin phi olur f degeri 2p nin herhangi carpani olarak degistirilebilir ve yine ayni aciyi verir burada radyan kullanildigina dikkat ediniz Bundan dolayi arg fonksiyonu bazen cok degerli olarak ifade edilir Fakat cogunlukla deger p p displaystyle pi pi veya 0 2p displaystyle 0 2 pi araliginda secilir Bu asil degerdir Karmasik sayilarin cesitli formlarda gosterilebilir Kutupsal form bir duzlemdeki noktanin tam konumunu belirten mutlak deger ve arguman bilesenleri olarak gosterilebilir soyle ki r f kutupsal ciftlerinden ozgun dikdortgenin koordinatlari olan x y rcos f rsin f displaystyle x y r cos varphi r sin varphi elde edildi Diger gosterimi z r cos f isin f displaystyle z r cos varphi i sin varphi buna trigonometrik form denir ve bazen r cis f olarak kisaltilir Euler formulu kullanilarak su sekilde gosterilebilir z reif displaystyle z re i varphi buna da ustel form denir Elektrik Muhendisligi nde daha cok acisal gosterim kullanimi yaygindir Bu gosterim A genlikli ve 8 fazina sahip fazoru ifade eder ve su sekilde yazilir A 8 Aej8 displaystyle A angle theta Ae j theta Acisal gosterimde 8 hem radyan hem de derece olabilir Elektrik akimini ifade eden i ile karistirmamak icin Elektrik Muhendisligi nde i yerine daha cok j kullanilir Kutupsal formdaki islemler Carpma ve bolme kutupsal formda temel formullere sahiptir r1eif1 r2eif2 r1r2ei f1 f2 displaystyle r 1 e i varphi 1 cdot r 2 e i varphi 2 r 1 r 2 e i varphi 1 varphi 2 ve r1eif1r2eif2 r1r2 ei f1 f2 displaystyle frac r 1 e i varphi 1 r 2 e i varphi 2 left frac r 1 r 2 right e i varphi 1 varphi 2 Bu formda her iki carpanin esitliklerin solundakiler katsayilari carpimin ozelliginden dolayi yan yana carpma isleminde veya alt alta bolme isleminde getirilebilirler Diger yandan uslu sayilarin kurallari geregi ifadeler ayni ise burada e displaystyle e bunlar ayni ifade altina alinirken carpma isleminde usler toplanir bolme isleminde ise usler cikartilir Us tam sayi ise soyle gosterilir r cos f isin f n rn cos nf isin nf displaystyle r cos varphi i sin varphi n r n cos n varphi i sin n varphi De Moivre formulu Sonuc olarak kutupsal formlar kokleri bulmak icinde kullanilabilir z herhangi karmasik sayi olmak uzere ve n pozitif tam sayi icin zn c olarak gosterilebilir Bu da cnin n koku diye okunur Eger c sifir degilse tam n tane farkli c nin koku vardir cebirin temel teoremine gore r gt 0 icin c re if de c nin n kokleri rnei f 2kpn k 0 1 n 1 displaystyle left sqrt n r e i left frac varphi 2k pi n right mid k in 0 1 ldots n 1 right Burada rn displaystyle sqrt n r pozitif reel sayi olan r nin genellikle pozitif olan n kokunu ifade eder Eger c 0 ise c nin tek bir koku vardir o da 0 dir Karmasik sayilarda islemKarmasik sayilarda cebirsel islemler gercel sayilarin genislemesidir Oncelikle iki karmasik sayinin esitligini verelim Esitlik Bir z a ib displaystyle z a mathbf i b ve w c id displaystyle w c mathbf i d karmasik sayilari icin z w displaystyle z w ancak a c displaystyle a c ve b d displaystyle b d iken gecerlidir bu dogru bir kavramdir Toplama Bir z a ib displaystyle z a mathbf i b ve w c id displaystyle w c mathbf i d karmasik sayilari icin z w a ib c id a c i b d displaystyle z w a mathbf i b c mathbf i d a c mathbf i b d Carpma Bir z a ib displaystyle z a mathbf i b ve w c id displaystyle w c mathbf i d karmasik sayilari icin zw a ib c id ac bd i bc ad displaystyle zw a mathbf i b c mathbf i d ac bd mathbf i bc ad Eslenik Bir karmasik sayi ile esleniginin karmasik uzaydaki gosterimi Bir z a ib displaystyle z a mathbf i b karmasik sayisi icin eslenik ifadesi i i displaystyle mathbf i mapsto mathbf i donusumudur ve z a ib displaystyle bar z a mathbf i b ya da matrislerde z zT ab ba displaystyle bar mathbf z mathbf z T begin bmatrix a amp b b amp a end bmatrix olarak tanimlanir Eslenigin cebirsel ozellikleri z w w z displaystyle overline z w overline w overline z z z displaystyle overline overline z z zw w z displaystyle overline zw overline w cdot overline z z w z w displaystyle overline z w overline z overline w z z displaystyle overline z z ancak z gercel sayi oldugunda gecerlidir Carpimsal ters Bir z a ib displaystyle z a mathbf i b karmasik sayisinin tersi ancak z 1 z zz z z 2 aa2 b2 iba2 b2 displaystyle z 1 frac bar z z bar z frac bar z z 2 a over a 2 b 2 mathbf i b over a 2 b 2 olarak ya da bir uygun olarak z 1 1detz ab ba aa2 b2ba2 b2 ba2 b2aa2 b2 displaystyle mathbf z 1 1 over det mathbf z begin bmatrix a amp b b amp a end bmatrix begin bmatrix a over a 2 b 2 amp b over a 2 b 2 b over a 2 b 2 amp a over a 2 b 2 end bmatrix oldugu gorulur Karmasik sayinin karekoku x i y 12 x x2 y2 i y sgn y x x2 y2 displaystyle sqrt x i y pm frac 1 sqrt 2 left sqrt x sqrt x 2 y 2 frac i y operatorname sgn y sqrt x sqrt x 2 y 2 right burada sgn a displaystyle operatorname sgn a Isaret fonksiyonudur Karmasik sayinin n dereceden koku Kok derecesi iki den buyuk olan karmasik sayilarin genel denklemi uzundur n sayisi artikca genel denklemde uzar Trigonometrik ve ustel bicim daha uygundur n 2 displaystyle n geqslant 2 icin tam sayi olmak uzere Ustel bicim x i yn x2 y22n ei arctan yx 2k p n displaystyle sqrt n x i y sqrt 2n x 2 y 2 e frac i arctan frac y x 2k pi n Trigonometrik bicim x i yn x2 y22n cos arctan yx 2k pn i sin arctan yx 2k pn displaystyle sqrt n x i y sqrt 2n x 2 y 2 left cos left frac arctan frac y x 2k pi n right i sin left frac arctan frac y x 2k pi n right right k 0 1 2 3 n 1 displaystyle k left 0 1 2 3 dots n 1 right kok derecesinin bir eksigi kadar sifirdan baslayarak tam sayilar verilebilir Bu da n dereceden alinan karmasik sayinin koklerini verir Ayrica bakinizKarmasik analiz Hiperbolik sayilar Cifte karmasik sayilar bicomplex numbers Quaternions Octonions Sayi sistemleri Karmasik C displaystyle mathbb C Reel R displaystyle mathbb R Rasyonel Q displaystyle mathbb Q Tam sayi Z displaystyle mathbb Z Dogal N displaystyle mathbb N Sifir 0Bir 1Asal sayilarBilesik sayilarNegatif tam sayilarKesir Devirli ondalik sayiIrrasyonel Cebirsel irrasyonelAskinSanalBasvuru ve KaynaklarNotlar Matematik ve Oyun Ali Nesin Nesin Yayincilik 2007 s 189 11 Ocak 2021 tarihinde kaynagindan Erisim tarihi 10 Ocak 2021 a b Andreescu Titu Andrica Dorin 17 Subat 2014 Complex Numbers from A to Z Ingilizce Springer Science amp Business Media ss 1 10 ISBN 978 0 8176 8415 0 KaynakcaA Mostowski amp M Stark Introduction to Higher Algebra Pergamon Press New York 1964 Matematik Dunyasi Dergisi s 64 73 8 Agustos 2020 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State