Matematikte, bir càdlàg fonksiyon (Fr. continue à droite, limite à gauche), gerçek sayıların bir altkümesi üzerinde tanımlı ve bu tanım kümesinin her noktasında sağdan sürekli, soldan limitli olan bir fonksiyondur. Cadlàg fonksiyonlar, özellikle sıçramaları olan stokastik süreçlerin incelenmesinde önemlidir. Bir tanım kümesi üzerindeki càdlàg fonksiyonların kümesine denir.
Càdlàg terimine benzeyen iki terim vardır. Bunlardan ilki olan càglàd (Fr. continue à gauche, limite à droite) fonksiyonda sol ve sağ yer değiştirmiştir. Yani, càglàd soldan sürekli, sağdan limitlidir. İkinci terim ise càllàl (Fr. continue à l'un, limite à l’autre) fonksiyondur. Bu terim kapsamında yön belirtilmeden bir taraftan sürekli diğer taraftan limitli fonksiyonlar tanımlanmıştır.
Tanım






vardır;
vardır ve
'ye eşittir.
Diğer deyişle, 
Örnekler
- Gerçel sayılar ya da bunların alt kümelerinde tanımlı sürekli fonksiyonların hepsi càdlàg fonksiyondur.
- Tanımları gereği, bütün kümülatif dağılım fonksiyonları càdlàg fonksiyondur.
- Bir tanımlanan her dışbükey fonksiyonun sağdan türevi artan bir càdlàg fonksiyondur.
Skorokhod uzayı



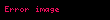


İlk önce karşılığı olan bir 

kümesini tanımlayalım. Her 
şeklinde tanımlayalım. Burada 








düzgün normunu tanımlayalım. Bu tanımlar ışığında, eğer 
- Ayrıştırılamadı (SVG (MathML, tarayıcı eklentisi aracılığıyla etkinleştirilebilir): Geçersiz yanıt ("Math extension cannot connect to Restbase.") sunucu "http://localhost:6011/tr.wikipedia.org/v1/":): {\displaystyle \sigma (f, g) := \inf_{\lambda \in \Lambda} \max \{ \| \lambda - I \|, \| f - g \circ \lambda \| \}, }
Skorokhod metriğini tanımlar. "Kıpırdama" sezgisi açısından konuşacak olursak, 
Skorokhod metriği gerçekten bir metriktir. 
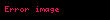
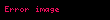
Skorokhod uzayının özellikleri
Düzgün topolojinin genelleştirilmesi

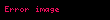
Tamlık
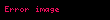

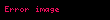

Ayrılabilirlik
Hem 

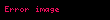
Skorokhod uzayındaki sıkılık
bir uygulaması aracılığıyla, Skorokhod uzayı Ayrıştırılamadı (SVG (MathML, tarayıcı eklentisi aracılığıyla etkinleştirilebilir): Geçersiz yanıt ("Math extension cannot connect to Restbase.") sunucu "http://localhost:6011/tr.wikipedia.org/v1/":): {\displaystyle \mathbb{D}} üzerindeki bir dizisi 
Cebirsel ve topolojik yapı
Skorokhod topolojisi ve fonksiyonların noktasal toplanması altında 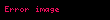




Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir cadlag fonksiyon Fr continue a droite limite a gauche gercek sayilarin bir altkumesi uzerinde tanimli ve bu tanim kumesinin her noktasinda sagdan surekli soldan limitli olan bir fonksiyondur Cadlag fonksiyonlar ozellikle sicramalari olan stokastik sureclerin incelenmesinde onemlidir Bir tanim kumesi uzerindeki cadlag fonksiyonlarin kumesine denir Cadlag terimine benzeyen iki terim vardir Bunlardan ilki olan caglad Fr continue a gauche limite a droite fonksiyonda sol ve sag yer degistirmistir Yani caglad soldan surekli sagdan limitlidir Ikinci terim ise callal Fr continue a l un limite a l autre fonksiyondur Bu terim kapsaminda yon belirtilmeden bir taraftan surekli diger taraftan limitli fonksiyonlar tanimlanmistir Tanimcadlag fonksiyonlarinin ornegidirler Kumulatif dagilim fonksiyonunun sayilabilir sonsuzlukta sureksizlik noktalarina sahip bir ornegi M d displaystyle M d bir metrik uzay ve E R displaystyle E subseteq mathbb R olsun f E M displaystyle f E to M fonksiyonuna asagidaki ozellikleri saglarsa cadlag fonksiyon denir Her t E displaystyle t in E icin f t lims t f s displaystyle f t lim s to t f s vardir f t lims t f s displaystyle f t lim s to t f s vardir ve f t displaystyle f t ye esittir Diger deyisle f displaystyle f fonksiyonu tanim kumesindeki her noktada sagdan surekli soldan limitlidir OrneklerGercel sayilar ya da bunlarin alt kumelerinde tanimli surekli fonksiyonlarin hepsi cadlag fonksiyondur Tanimlari geregi butun kumulatif dagilim fonksiyonlari cadlag fonksiyondur Bir tanimlanan her disbukey fonksiyonun sagdan turevi artan bir cadlag fonksiyondur Skorokhod uzayiE displaystyle E den M displaystyle M ye tanimli tum cadlag fonksiyonlarinin kumesi genellikle D E M displaystyle mathbb D E M veya sadece D displaystyle mathbb D ile gosterilir ve bu kumeye Ukraynali matematikci a atfen Skorokhod uzayi adi verilir Skorokhod uzayina sezgisel olarak uzay ve zamani biraz oynatmamiza izin veren bir topoloji atanabilir oysaki duzgun yakinsamanin geleneksel topolojisi yalnizca uzayi biraz oynatmamiza izin verir Basitlestirmek icin mesela E 0 T displaystyle E 0 T ve M Rn displaystyle M mathbb R n alalim Ilk once karsiligi olan bir ϖf d displaystyle varpi f delta tanimlamamiz gerekecek Herhangi bir F E displaystyle F subseteq E icin wf F sups t F f s f t displaystyle w f F sup s t in F f s f t kumesini tanimlayalim Her d gt 0 displaystyle delta gt 0 icinse cadlag modulunu ϖf d infPmax1 i kwf ti 1 ti displaystyle varpi f delta inf Pi max 1 leq i leq k w f t i 1 t i seklinde tanimlayalim Burada mini ti ti 1 gt d displaystyle min i t i t i 1 gt delta ve k N displaystyle k in mathbb N olacak sekilde tanimlanan butun P 0 t0 lt t1 lt lt tk T displaystyle Pi 0 t 0 lt t 1 lt dots lt t k T parcalanislari uzerinden tanimlanmaktadir Sureksiz fonksiyonlar icin tanimlanan sureklilik modulu ne kadar makul ise buradaki tanim da cadlag olmayan fonksiyonlar icin en azindan o kadar makuldur O zaman f displaystyle f cadlag fonksiyondur ancak ve ancak limd 0ϖf d 0 displaystyle lim delta to 0 varpi f delta 0 E displaystyle E uzerinden yine E displaystyle E ye tanimli kesin artan surekli birebir orten fonksiyonlarin kumesi L displaystyle Lambda olsun bunlar zaman icindeki kipirdanmalar olacak E displaystyle E uzerinde tanimli fonksiyonlar icin f supt E f t displaystyle f sup t in E f t duzgun normunu tanimlayalim Bu tanimlar isiginda eger I E E displaystyle I E to E ozdeslik birim fonksiyonu ise Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle f g in mathbb D icin Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle sigma f g inf lambda in Lambda max lambda I f g circ lambda Skorokhod metrigini tanimlar Kipirdama sezgisi acisindan konusacak olursak l I displaystyle lambda I zamandaki kipirdamanin boyutunu olcer Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle f g circ lambda ise uzaydaki kipirdamanin buyuklugunu olcer Skorokhod metrigi gercekten bir metriktir s displaystyle sigma tarafindan uretilen S displaystyle Sigma topolojisine D displaystyle mathbb D deki Skorokhod topolojisi adi verilir Skorokhod uzayinin ozellikleri Duzgun topolojinin genellestirilmesi E displaystyle E uzerinde tanimli surekli fonksiyonlarin uzayi olan Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle C D displaystyle mathbb D nin bir altuzayidir Skorokhod topolojisi Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle C ye gore dusunulurse o zaman oradaki duzgun topolojilerle aynidir Tamlik D displaystyle mathbb D Skorokhod metrigi s displaystyle sigma altinda tam uzay degildir Yine de D displaystyle mathbb D yi tam yapacak ve topolojik olarak denk bir s0 displaystyle sigma 0 metrigi vardir Ayrilabilirlik Hem s0 displaystyle sigma 0 hem de s displaystyle sigma acisindan D displaystyle mathbb D bir uzaydir Bu yuzden Skorokhod uzayi Skorokhod uzayindaki sikilik bir uygulamasi araciligiyla Skorokhod uzayi Ayristirilamadi SVG MathML tarayici eklentisi araciligiyla etkinlestirilebilir Gecersiz yanit Math extension cannot connect to Restbase sunucu http localhost 6011 tr wikipedia org v1 displaystyle mathbb D uzerindeki bir dizisi mn n 1 2 displaystyle mu n n 1 2 dots ancak ve ancak asagidaki su kosullar saglanirsa lima lim supn mn f D f a 0 displaystyle lim a to infty limsup n to infty mu n big f in mathbb D f geq a big 0 limd 0lim supn mn f D ϖf d e 0 e gt 0 displaystyle lim delta to 0 limsup n to infty mu n big f in mathbb D varpi f delta geq varepsilon big 0 quad forall varepsilon gt 0 Cebirsel ve topolojik yapi Skorokhod topolojisi ve fonksiyonlarin noktasal toplanmasi altinda D displaystyle mathbb D az sonra verilecek ornekte gorulebilecegi gibi topolojik bir grup degildir Gercekten de E 0 2 displaystyle E 0 2 olsun ve fn x 1 1 n 2 D displaystyle f n chi 1 1 n 2 in mathbb D de bir karakteristik fonksiyonlar dizisi olsun Skorokhod topolojisinde fn x 1 2 displaystyle f n rightarrow chi 1 2 olmasina ragmen fn x 1 2 displaystyle f n chi 1 2 dizisi 0 a yakinsamaz Ayrica bakinizKaynakca Skorokhod space Encyclopedia of Mathematics 27 Temmuz 2024 tarihinde kaynagindan arsivlendi Erisim tarihi 9 Eylul 2024 a b Billingsley P Convergence of Probability Measures New York Wiley
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State







