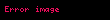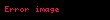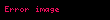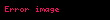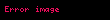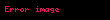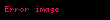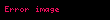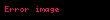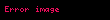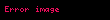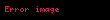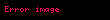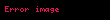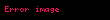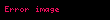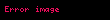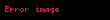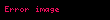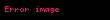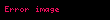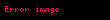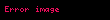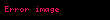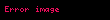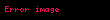Matematik'te, beta fonksiyonu, Euler integrali'nin ilk türüdür,


için bu özel fonksiyon'unun tanımı
Beta fonksiyonu tarafından öğrencileri Euler ve Legendre'ye adandı.
Özellikler
Beta fonksiyonu 'tir, yani
yerine konulan Birçok diğer formları da vardır:
Burada 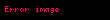
özellikle eşitlikteki ikinci gösterimden elde edilen buradaki eşitliklerden bazıları, mesela trigonometrik formül,
.
.
'daki 'ne uygulanabilir .
Sadece tam sayılar için yazılan gama fonksiyonu faktöriyel'dir, beta fonksiyonu endeksi tarafından tanımlanabilir:
Ayrıca her 
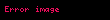

İlk kez , sicim teorisi'deki, varsayımında beta fonksiyonunu kullandı.
Beta ve Gama fonksiyonları arasındaki ilişki
Beta fonksiyonunun türetilen iki faktöriyel yazılarak integral gösterimi;
Şimdi, 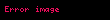
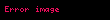
Kutupsal koordinatlara dönüşümü 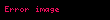
Dolayısıyla,beta fonksiyonunun kullanılan formu ve değişkenleri yeniden:
Diğer bir türetim,bir özel durumu için konvolüsyon integrali alınırsa
and
, sonuç kolayca:
.
Türevleri
türevleri sırasıyla:
burada 
Integralleri
beta fonksiyonunun kontür integral içeren şeklidir .
Yaklaşıklıklar
Asimptotik formül,'nı verir.
x büyük y büyük ise,
diğer bir durumx büyük ve y sabit ise,
Tamamlanmamış beta fonksiyonu
Tamamlanmamış demek integralin bir sinirinin kapali(burada 0dan x'a) diğer sinirinin açik olmasi demektir. Beta fonksiyonunun bir genellemesi Tamamlanmamış beta fonksiyonu 'dur.
Tanımı
x = 1, için tamamlanmamış beta fonksiyonu ile tamamlanmış beta fonksiyonu çakışır.Bu ilişki gama fonksiyonu ve genel şekli tamamlanmamış gama fonksiyonu arasında da vardır..
düzenlenmiş,tamamlanmamış beta fonksiyonu (veya kısaca düzenlenmiş beta fonksiyonu) şeklinde tanımlanan bu iki fonksiyonun terimleri:
a ve b tam sayı değerleri için bilinen integral dışında ( kullanılabilir):
Binom dağılımı'nın, bir rastgele değişkeni X " başarı olasılığı" p örnekleme boyutu n olmak üzere için değerlendirmede; Düzenlenmiş- tamamlanmamış beta fonksiyonu kullanılabilir ve burada :
Özellikler
(Listede diğer birçok özellikler olabilir.)
Ayrıca bakınız
- Matematiksel fonksiyonların listesi
- Beta dağılımı
- Binom dağılımı
- ,sonlu alanlar üzerinde beta fonksiyonunun analogları.
- Negatif binom dağılımı
- Gama fonksiyonu
Kaynakça
- M. Zelen and N. C. Severo. in Milton Abramowitz and Irene A. Stegun, eds. with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See §6.2, 6.6, and 26.5)24 Mayıs 2008 tarihinde Wayback Machine sitesinde .
- W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling. in C. Cambridge, UK: Cambridge University Press, 1992. Second edition. (See section 6.4)
- Beta fonksiyonu, PlanetMath.org.
- Arbitrarily accurate values can be obtained from The Wolfram Functions Site10 Ekim 2007 tarihinde Wayback Machine sitesinde ., Evaluate Beta Regularized Incomplete beta 14 Haziran 2020 tarihinde Wayback Machine sitesinde .
Dış bağlantılar
- Cephes8 Aralık 2009 tarihinde Wayback Machine sitesinde . - C and C++ language special functions math library
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik te beta fonksiyonu Euler integrali nin ilk turudur Re x Re y gt 0 displaystyle textrm Re x textrm Re y gt 0 beta fonksiyonununPozitif x ve y degerleri icin beta fonksiyonunun bir cizimi icin bu ozel fonksiyon unun tanimi B x y 01tx 1 1 t y 1dt displaystyle mathrm mathrm B x y int 0 1 t x 1 1 t y 1 dt Beta fonksiyonu tarafindan ogrencileri Euler ve Legendre ye adandi OzelliklerBeta fonksiyonu tir yani B x y B y x displaystyle mathrm B x y mathrm B y x yerine konulan Bircok diger formlari da vardir B x G x 2G 2x displaystyle mathrm B x dfrac Gamma x 2 Gamma 2x B x y G x G y G x y displaystyle mathrm B x y dfrac Gamma x Gamma y Gamma x y B x y 2 0p 2 sin 8 2x 1 cos 8 2y 1d8 Re x gt 0 Re y gt 0 displaystyle mathrm B x y 2 int 0 pi 2 sin theta 2x 1 cos theta 2y 1 d theta qquad textrm Re x gt 0 textrm Re y gt 0 B x y 0 tx 1 1 t x ydt Re x gt 0 Re y gt 0 displaystyle mathrm B x y int 0 infty dfrac t x 1 1 t x y dt qquad textrm Re x gt 0 textrm Re y gt 0 B x y n 0 n yn x n displaystyle mathrm B x y sum n 0 infty dfrac n y choose n x n B x y x yxy n 1 1 xyn x y n 1 displaystyle mathrm B x y frac x y xy prod n 1 infty left 1 dfrac xy n x y n right 1 B x y B x y 1 y pxsin py displaystyle mathrm B x y cdot mathrm B x y 1 y dfrac pi x sin pi y Burada G displaystyle Gamma gama fonksiyonu dur ozellikle esitlikteki ikinci gosterimden elde edilen buradaki esitliklerden bazilari mesela trigonometrik formul G 1 2 p displaystyle Gamma 1 2 sqrt pi B 1 2 p displaystyle mathrm B 1 2 pi daki ne uygulanabilir Sadece tam sayilar icin yazilan gama fonksiyonu faktoriyel dir beta fonksiyonu endeksi tarafindan tanimlanabilir nk 1 n 1 B n k 1 k 1 displaystyle n choose k frac 1 n 1 mathrm B n k 1 k 1 Ayrica her n displaystyle n tam sayisi icin B displaystyle mathrm B nin k displaystyle k surekli degerleri icin oteleme fonksiyonu kapali formunun integrallenmis sekli nk 1 nn sin pk p i 0n k i displaystyle n choose k 1 n n cfrac sin pi k pi prod i 0 n k i Ilk kez sicim teorisi deki varsayiminda beta fonksiyonunu kullandi Beta ve Gama fonksiyonlari arasindaki iliskiBeta fonksiyonunun turetilen iki faktoriyel yazilarak integral gosterimi G x G y 0 e uux 1du 0 e vvy 1dv displaystyle Gamma x Gamma y int 0 infty e u u x 1 du int 0 infty e v v y 1 dv Simdi u a2 displaystyle u equiv a 2 v b2 displaystyle v equiv b 2 yazalim boylece G x G y 4 0 e a2a2x 1da 0 e b2b2y 1db e a2 b2 a 2x 1 b 2y 1dadb displaystyle begin aligned Gamma x Gamma y amp 4 int 0 infty e a 2 a 2x 1 mathrm d a int 0 infty e b 2 b 2y 1 db amp int infty infty int infty infty e a 2 b 2 a 2x 1 b 2y 1 da db end aligned Kutupsal koordinatlara donusumu a rcos 8 displaystyle a r cos theta b rsin 8 displaystyle b r sin theta G x G y 02p 0 e r2 rcos 8 2x 1 rsin 8 2y 1rdrd8 0 e r2r2x 2y 2rdr 02p cos 8 2x 1 sin 8 2y 1 d8 12 0 e r2r2 x y 1 d r2 4 0p 2 cos 8 2x 1 sin 8 2y 1d8 G x y 2 0p 2 cos 8 2x 1 sin 8 2y 1d8 G x y B x y displaystyle begin aligned Gamma x Gamma y amp int 0 2 pi int 0 infty e r 2 r cos theta 2x 1 r sin theta 2y 1 r dr d theta amp int 0 infty e r 2 r 2x 2y 2 r dr int 0 2 pi cos theta 2x 1 sin theta 2y 1 d theta amp frac 1 2 int 0 infty e r 2 r 2 x y 1 d r 2 4 int 0 pi 2 cos theta 2x 1 sin theta 2y 1 d theta amp Gamma x y 2 int 0 pi 2 cos theta 2x 1 sin theta 2y 1 d theta amp Gamma x y mathrm B x y end aligned Dolayisiyla beta fonksiyonunun kullanilan formu ve degiskenleri yeniden B x y G x G y G x y displaystyle mathrm B x y frac Gamma x Gamma y Gamma x y Diger bir turetim bir ozel durumu icin konvolusyon integrali alinirsa f u e uux 11R displaystyle f u e u u x 1 1 mathbb R and g u e uuy 11R displaystyle g u e u u y 1 1 mathbb R sonuc kolayca G x G y Rf u du Rg u du R f g u du B x y G x y displaystyle Gamma x Gamma y left int mathbb R f u du right left int mathbb R g u du right int mathbb R f g u du mathrm B x y Gamma x y Turevleriturevleri sirasiyla xB x y B x y G x G x G x y G x y B x y ps x ps x y displaystyle partial over partial x mathrm B x y mathrm B x y left Gamma x over Gamma x Gamma x y over Gamma x y right mathrm B x y psi x psi x y burada ps x displaystyle psi x digama fonksiyonu dur Integralleribeta fonksiyonunun kontur integral iceren seklidir YaklasikliklarAsimptotik formul ni verir x buyuk y buyuk ise B x y 2pxx 12yy 12 x y x y 12 displaystyle mathrm B x y sim sqrt 2 pi frac x x frac 1 2 y y frac 1 2 left x y right x y frac 1 2 diger bir durumx buyuk ve y sabit ise B x y G y x y displaystyle mathrm B x y sim Gamma y x y Tamamlanmamis beta fonksiyonuTamamlanmamis demek integralin bir sinirinin kapali burada 0dan x a diger sinirinin acik olmasi demektir Beta fonksiyonunun bir genellemesi Tamamlanmamis beta fonksiyonu dur Tanimi B x a b 0xta 1 1 t b 1dt displaystyle mathrm B x a b int 0 x t a 1 1 t b 1 dt x 1 icin tamamlanmamis beta fonksiyonu ile tamamlanmis beta fonksiyonu cakisir Bu iliski gama fonksiyonu ve genel sekli tamamlanmamis gama fonksiyonu arasinda da vardir duzenlenmis tamamlanmamis beta fonksiyonu veya kisaca duzenlenmis beta fonksiyonu seklinde tanimlanan bu iki fonksiyonun terimleri Ix a b B x a b B a b displaystyle I x a b dfrac mathrm B x a b mathrm B a b a ve b tam sayi degerleri icin bilinen integral disinda kullanilabilir Ix a b j aa b 1 a b 1 j a b 1 j xj 1 x a b 1 j displaystyle I x a b sum j a a b 1 a b 1 over j a b 1 j x j 1 x a b 1 j Binom dagilimi nin bir rastgele degiskeni X basari olasiligi p ornekleme boyutu n olmak uzere icin degerlendirmede Duzenlenmis tamamlanmamis beta fonksiyonu kullanilabilir ve burada F k n p Pr X k I1 p n k k 1 displaystyle F k n p Pr X leq k I 1 p n k k 1 Ozellikler I0 a b 0 displaystyle I 0 a b 0 I1 a b 1 displaystyle I 1 a b 1 Ix a b 1 I1 x b a displaystyle I x a b 1 I 1 x b a Listede diger bircok ozellikler olabilir Ayrica bakinizMatematiksel fonksiyonlarin listesi Beta dagilimi Binom dagilimi sonlu alanlar uzerinde beta fonksiyonunun analoglari Negatif binom dagilimi Gama fonksiyonuKaynakcaM Zelen and N C Severo in Milton Abramowitz and Irene A Stegun eds with Formulas Graphs and Mathematical Tables New York Dover 1972 See 6 2 6 6 and 26 5 24 Mayis 2008 tarihinde Wayback Machine sitesinde W H Press B P Flannery S A Teukolsky W T Vetterling in C Cambridge UK Cambridge University Press 1992 Second edition See section 6 4 Beta fonksiyonu PlanetMath org Arbitrarily accurate values can be obtained from The Wolfram Functions Site10 Ekim 2007 tarihinde Wayback Machine sitesinde Evaluate Beta Regularized Incomplete beta 14 Haziran 2020 tarihinde Wayback Machine sitesinde Dis baglantilarCephes8 Aralik 2009 tarihinde Wayback Machine sitesinde C and C language special functions math library
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State