Matematiğin alt dalı olan analizde ve olasılık kuramında, bir σ-cebiri ("sigma cebiri"; ayrıca σ-cismi olarak da adlandırılır; burada σ harfi Almanca "Summe" kelimesinden gelir) bir X kümesi üzerinde, X in altkümelerinden oluşan ve boş olmayan, , sayılabilir birleşimler ve sayılabilir kesişimler altında bir Σ kümeler kümesidir. sıralı ikilisi ölçülebilir uzay olarak adlandırılır.
Altkümelerden oluşan bir σ-cebiri, bir ; bu ikinci türdeki elemanların yalnızca sonlu sayıda altkümenin birleşimi veya kesişimi altında kapalı olması yeterlidir ki bu da daha zayıf bir koşuldur.
σ-cebirlerinin en temel kullanım alanı ölçülerin tanımlanmasındadır; özellikle, belirli bir ölçünün tanımlandığı altkümelerin kümesinin bir σ-cebiri olması gerekliliği vardır. Ölçü kavramı, Lebesgue integralinin temeli olarak analizde ve olasılık kuramında, olasılık atfedilebilen olayların kümesi olarak yorumlandığında önemlidir. Ayrıca olasılıkta, σ-cebirleri koşullu beklenti tanımında da kilit rol oynar.
İstatistikte, (alt) σ-cebirleri biçimsel matematiksel tanımı için gereklidir. Bu gereklilik, bahsedilen istatistik, özellikle bir fonksiyon veya rasgele bir süreç olduğunda ve kavramı uygulanabilir olmadığında ortaya çıkar.
Örnek vermek gerekirse, ise, üzerinde tanımlı olabilecek σ-cebirlerinden biri şeklindedir. Burada , boş kümeyi temsil eder. Genel olarak, sonlu bir cebir her zaman bir σ-cebiridir.
Eğer , kümesinin sayılabilir bir ise, bu bölmelemedeki kümelerin tüm birleşimlerinden (boş küme dahil) oluşan küme de bir σ-cebiridir.
Daha anlamlı ve yaygın bir örnek, gerçel sayı doğrusu üzerindeki başlayan, sonra tüm sayılabilir birleşimler, sayılabilir kesişimler ve küme farkları eklenerek (bu işlem üzerinden yapılan ile devam ettirilir) ilgili kapalılık özellikleri sağlanana kadar genişletilen altkümeler kümesidir. Bu yapıya denir.
Motivasyon
σ-cebirleri için en az üç temel motivasyon vardır: ölçülerin tanımlanması, kümelerin limitlerinin işlenmesi ve kümelerle karakterize edilen kısmi bilginin yönetilmesi.
Ölçü
Bir X kümesi üzerinde tanımlı bir ölçü, X'in altkümelerine sıfır ya da pozitif bir gerçel sayı atayan bir fonksiyondur. Ölçü kavramı kümeler için "büyüklük" ya da "hacim" kavramlarının matematiksel dil ve hassasiyet içinde tanımlanması olarak düşünülebilir. Ayrık kümelerin birleşimlerinin ölçüsünün, bu kümelerin ölçülerinin toplamı olmasını istenir ki bu durum ayrık kümeler için sonsuz dizilerde bile geçerli olmalıdır.
X kümesinin her altkümesine bir ölçü atamak istenebilir; ancak, birçok doğal durumda bu mümkün değildir. Örneğin, seçim aksiyomu, gerçel doğru üzerindeki uzunluk kavramı altında bazı kümelere ölçü atamanın mümkün olmadığını söyler. Bu duruma örnek olarak verilebilir. Bu nedenle, bunun yerine X'in ayrıcalıklı bir altküme ailesi olan daha küçük bir küme ailesi dikkate alınır. Bu ailedeki altkümelere ölçülebilir kümeler denir. Ölçülebilir kümeler, doğal olarak şu işlemler altında kapalıdır: bir ölçülebilir kümenin tümleyeni yine ölçülebilir olmalıdır, ve ölçülebilir kümelerin sayılabilir birleşimi de ölçülebilir olmalıdır. Bu özelliklere sahip boş olmayan küme koleksiyonlarına σ-cebiri denir.
Kümelerin limitleri
Ölçü kavramının birçok kullanımında, örneğin olasılıktaki gibi durumlarda, kümelerin dizilerinin limitleri önemlidir. Bu tür limitler için, sayılabilir birleşimler ve kesişimler altında kapalı olma özelliği çok önemlidir. σ-cebirleri üzerinde küme limitleri şu şekilde tanımlanır:
'teki
gibi altkümeler dizisi için en küçük üst limit ya da dış limit,





- Aynı dizi için en büyük alt limit ya da iç limit,




Her zaman, 


Alt σ-cebirler
Olasılığın birçok kısmında, özellikle koşullu beklenti söz konusu olduğunda, gözlemlenebilecek tüm bilgilerin yalnızca bir kısmını temsil eden kümeler dikkate alınır. Bu kısmi bilgi, asıl σ-cebirin bir altkümesi olan daha küçük bir σ-cebiri ile tanımlanabilir; bu alt σ-cebiri yalnızca kısmi bilgiye göre belirlenebilen kümelerden oluşur. Biçimsel olarak, 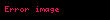



Bu fikri açıklamak basit örnekler yararlı olacaktır:
İki kişinin yazı-tura atarak oynadığı ve sonsuza dek sürebilecek bir oyun oynadığını hayal edelim. Her iki oyuncunun da sonsuz zengin olduğu varsayımı altında oyuna süresiz bir şekilde devam edilebilir. Bu durumda, örneklem uzayı Ω, sonsuz sayıda yazı-tura sonucunu temsil eden dizilerden oluşur: 
İlk n atıştan sonra gözlemlenen bilgi, ilk n yazı-tura sonucunu açıklayan 

Bu yapı ilk n yazı-tura atışını sabitlemektedir ama kalan sonuçlara dair herhangi bir bilgi içermemektedir. Bu durumda, 

Tanım ve özellikler
Tanım
Bir X kümesi verilsin ve 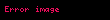

olmalıdır.
, tümleyene göre kapalıdır: Eğer
ise,
da
içindedir.
, sayılabilir birleşimlere göre kapalıdır: Eğer
ise, o hâlde
da
içindedir.
Bu özelliklerden, σ-cebirinin aynı zamanda sayılabilir kesişimlere göre de kapalı olduğu sonucu çıkar ki bu durum De Morgan yasası yardımıyla gösterilebilir.
Ayrıca, 


Bir σ-cebirin elemanları ölçülebilir kümeler olarak adlandırılır. 

Bir σ-cebiri hem bir hem de bir (veya λ-sistemi). Tersi de yine 'ne göre doğrudur.
Dynkin π-λ teoremi
Bu teorem (ya da ilişkili olan ) belirli σ-cebirlerinin özelliklerine dair birçok sonucun ispatında kullanılan temel bir araçtır. Bu teorem, iki daha basit küme sınıfının doğasını kullanır:
- Bir
, sonlu sayıda kümenin kesişimi altında kapalı olan altkümeler kümesidir.
- Bir (ya da λ-sistemi)
,
kümesini içeren ve göre ve ayrık altkümelerin sayılabilir birleşimleri altında kapalı olan altkümeler kümesidir.
Dynkin π-λ teoremi ise şunu ifade eder: eğer 






Bazı π-sistemleri oldukça basit küme sınıflarından oluştuğu için, 



Bu teoremin en temel kullanım alanlarından biri, ayrı ayrı tanımlanmış ölçülerin veya integrallerin eşdeğerliğini göstermektir. Örneğin, bu teorem rasgele bir değişken 








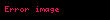
σ-cebirlerinin birleştirilmesi
Varsayalım ki 

Kesişim Bir σ-cebiri ailesinin kesişimi yine bir σ-cebiridir. Bu özellik vurgulanmak istendiğinde, şu şekilde gösterilir: 
İspat taslağı: 






Birleşim σ-cebirlerinin birleşimi genel olarak ne bir σ-cebiridir ne de bir cebirdir; ancak bu birleşim, bir σ-cebiri . Bu σ-cebire birleştirme (join) denir ve genellikle şöyle gösterilir: 
Bu birleştirmeyi üreten bir şu şekilde ifade edilir: 
İspat taslağı: 


Bu durumdan: 

Öte yandan, 

Alt uzaylar için σ-cebirleri
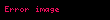


ailesi,
kümesinin altkümelerinden oluşan bir σ-cebiridir.
ölçülebilir bir uzay olmak üzere,
ailesi,
kümesinin altkümelerinden oluşan bir σ-cebiridir.
σ-halka ile ilişkisi
Bir σ-cebiri 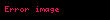

Her σ-cebiri aynı zamanda bir σ-halkadır; ancak her σ-halka bir σ-cebiri olmak zorunda değildir. Örneğin, gerçel doğru üzerindeki sıfır sahip tüm ölçülebilir kümeler bir σ-halka oluşturur, fakat bu kümeler gerçel doğrunun tamamını kapsayamayacağı için bir σ-cebiri oluşturmazlar; çünkü, gerçel doğrunun ölçüsü sonsuzdur ve bu kümelerin sayılabilir birleşimiyle elde edilemez.
Buna karşılık, sonlu ölçüye sahip Lebesgue ölçülebilir kümelerin oluşturduğu aile bir , fakat bir σ-halka değildir; çünkü, bu kümelerin sayılabilir birleşimi gerçel doğruyu verebilir. Ancak, toplam ölçü sonlu olmayabilir.
Tipografik not
σ-cebirleri, bazen büyük harflerle veya gösterilir. Bu nedenle 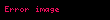


Önemli durumlar ve örnekler
Ayrılabilir σ-cebirler
Bir ayrılabilir σ-cebiri (ya da ayrılabilir σ-cismi), özelliği taşıyan ve sonlu bir 



Sayılabilir bir küme ailesi tarafından oluşturulan her σ-cebiri ayrılabilirdir; ancak bunun tersi doğru olmayabilir. Örneğin, ayrılabilirdir (çünkü her Lebesgue ölçülebilir küme bir ile ölçü bakımından eşdeğerdir), fakat sayılabilir olarak üretilemez (çünkü kardinalitesi süreyden büyüktür).
Ayrılabilir bir ölçü uzayı, onu yapan doğal bir yapısına sahiptir. Bu durumda iki küme arasındaki uzaklık, bu kümelerin simetrik farkının ölçüsüne eşittir. Ancak simetrik farkın ölçüsü sıfır olan farklı kümeler olabileceğinden, bu uzaklık bir gerçek metrik oluşturmaz. Bununla birlikte, ölçüsü sıfır olan farklara sahip kümeleri bir olarak tanımlarsak, oluşan üzerinde gerçek bir metrik tanımlanabilir. Eğer ölçü uzayı ayrılabilirse, elde edilen metrik uzayın da ayrılabilir olduğu gösterilebilir.
Basit küme temelli örnekler
Herhangi bir 
- Yalnızca boş küme ve
kümesini içeren aile,
üzerindeki en küçük (aşikar) σ-cebiridir:
.
kümesinin , yani tüm altkümelerinin kümesi, ayrık σ-cebiri (ya da tam σ-cebiri) olarak adlandırılır.
ailesi,
altkümesinin oluşturduğu basit bir σ-cebiridir.
kümesinin olduğu varsayılırsa,
’in sayılabilir olan (ya da tümleyeni sayılabilir olan) tüm altkümelerinden oluşan küme bir σ-cebiridir. Bu σ-cebiri,
’in elemanlarının oluşturduğu σ-cebiridir. "Sayılabilir" kavramı burada sonlu ya da boş kümeleri de içermektedir.
’in sayılabilir bir verilmişse, bu bölmeyi oluşturan kümelerin tüm birleşimlerinden (boş küme dahil) oluşan küme bir σ-cebiridir.
Durdurma zamanı σ-cebirleri
Bir 

Bu σ-cebiri, bir süzgeç yapısına sahip olasılık uzayında, rasgele bir zaman 


Küme aileleri tarafından oluşturulan σ-cebirleri
Herhangi bir küme ailesi tarafından oluşturulan σ-cebiri






Eğer 



Basit bir örnek olarak, 


açısından, yalnızca bir kümeden oluşan 




Kullanışlı birçok σ-cebiri, farklı kümeler ailelerinden oluşturulur. Bazı yaygın örnekler aşağıda verilmiştir.
Bir fonksiyon tarafından oluşturulan σ-cebiri
Eğer 






Yani 


Bir 



En sık karşılaşılan durum, 


Özellikle 




Yararlı bir özellik ise şöyledir: Varsayalım 









Standart örnekler arasında şunlar vardır:
üzerindeki Borel σ-cebiri
üzerindeki silindir σ-cebiri (aşağıda tanımlanmıştır)
Borel ve Lebesgue σ-cebirleri
Önemli bir örnek, herhangi bir topolojik uzay üzerindeki Borel cebiridir: Bu, açık kümeler (ya da eşdeğer biçimde kapalı kümeler) tarafından oluşturulan σ-cebiridir. Bu σ-cebir, genellikle topolojik uzayın değildir. Aşikar olmayan kümelere örnek olarak veya verilebilir.


Çarpım σ-cebiri




Buradaki 


Her iki durumda da, kullanılan üreteç kümeler ailesi bir π-sistemidir.
Silindir kümeleri tarafından oluşturulan σ-cebiri
Varsayalım ki 


Her 


Daha sonra, bu π-sistemlerinin tüm zaman indeksleri 


Bu σ-cebir, 
Önemli bir özel durum, 



Yuvar σ-cebiri
Yuvar σ-cebiri, bir metrik uzayda tüm açık (veya kapalı) içeren en küçük σ-cebiridir. Bu σ-cebir, hiçbir zaman daha büyük değildir.
Not edilmelidir ki ayrılabilir uzaylar için Borel σ-cebiri ile yuvar σ-cebiri aynıdır. Ancak, bazı , bazı fonksiyonlar Borel ölçülebilir değildir ama yuvar σ-cebirine göre ölçülebilirdir. Bu durum, özellikle böyle uzaylarda tanımlı fonksiyonların analizi için yuvar σ-cebirinin kullanılmasını değerli kılar.
Bir rasgele değişken veya vektör tarafından oluşturulan σ-cebiri
Varsayalım ki 
Eğer 


Bu durumda, 

Bir rasgele süreç tarafından oluşturulan σ-cebiri
Varsayalım ki 

Eğer 



Bu durumda, 

Ayrıca bakınız
Kaynakça
- ^ Elstrodt, J. (2018). Maß- Und Integrationstheorie. Springer Spektrum Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-57939-8
- ^ "11. Ölçülebilir Uzaylar". Random: Probability, Mathematical Statistics, Stochastic Processes. University of Alabama in Huntsville, Department of Mathematical Sciences. 30 Ocak 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 30 Mart 2016.
Bir σ-cebiri aynı zamanda bir cebirdir, dolayısıyla cebirler için geçerli temel sonuçlar burada da geçerlidir.
- ^ (2012). Probability and Measure. Anniversary. Wiley. ISBN .
- ^ (1987). Real & Complex Analysis. McGraw-Hill. ISBN .
- ^ Vestrup, Eric M. (2009). The Theory of Measures and Integration. John Wiley & Sons. s. 12. ISBN .
- ^ Džamonja, Mirna; (1995). "Properties of the class of measure separable compact spaces" (PDF). Fundamenta Mathematicae. s. 262. 7 Mayıs 2024 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 28 Mart 2025.
- ^ Fischer, Tom (2013). "On simple representations of stopping times and stopping time sigma-algebras". Statistics and Probability Letters. 83 (1). ss. 345-349. arXiv:1112.1603 $2. doi:10.1016/j.spl.2012.09.024.
- ^ (2001). Foundations of Modern Probability. 2nd. . s. 7. ISBN .
- ^ van der Vaart, A. W., & Wellner, J. A. (1996). Weak Convergence and Empirical Processes. In Springer Series in Statistics. Springer New York. https://doi.org/10.1007/978-1-4757-2545-2
Dış bağlantılar
- Hazewinkel, Michiel, (Ed.) (2001), "Kümeler Cebiri", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- Sigma Cebiri – PlanetMath sitesinden.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin alt dali olan analizde ve olasilik kuraminda bir s cebiri sigma cebiri ayrica s cismi olarak da adlandirilir burada s harfi Almanca Summe kelimesinden gelir bir X kumesi uzerinde X in altkumelerinden olusan ve bos olmayan sayilabilir birlesimler ve sayilabilir kesisimler altinda bir S kumeler kumesidir X S displaystyle X Sigma sirali ikilisi olculebilir uzay olarak adlandirilir Altkumelerden olusan bir s cebiri bir bu ikinci turdeki elemanlarin yalnizca sonlu sayida altkumenin birlesimi veya kesisimi altinda kapali olmasi yeterlidir ki bu da daha zayif bir kosuldur s cebirlerinin en temel kullanim alani olculerin tanimlanmasindadir ozellikle belirli bir olcunun tanimlandigi altkumelerin kumesinin bir s cebiri olmasi gerekliligi vardir Olcu kavrami Lebesgue integralinin temeli olarak analizde ve olasilik kuraminda olasilik atfedilebilen olaylarin kumesi olarak yorumlandiginda onemlidir Ayrica olasilikta s cebirleri kosullu beklenti taniminda da kilit rol oynar Istatistikte alt s cebirleri bicimsel matematiksel tanimi icin gereklidir Bu gereklilik bahsedilen istatistik ozellikle bir fonksiyon veya rasgele bir surec oldugunda ve kavrami uygulanabilir olmadiginda ortaya cikar Ornek vermek gerekirse X a b c d displaystyle X a b c d ise X displaystyle X uzerinde tanimli olabilecek s cebirlerinden biri S a b c d a b c d displaystyle Sigma varnothing a b c d a b c d seklindedir Burada displaystyle varnothing bos kumeyi temsil eder Genel olarak sonlu bir cebir her zaman bir s cebiridir Eger A1 A2 A3 displaystyle A 1 A 2 A 3 ldots X displaystyle X kumesinin sayilabilir bir ise bu bolmelemedeki kumelerin tum birlesimlerinden bos kume dahil olusan kume de bir s cebiridir Daha anlamli ve yaygin bir ornek gercel sayi dogrusu uzerindeki baslayan sonra tum sayilabilir birlesimler sayilabilir kesisimler ve kume farklari eklenerek bu islem uzerinden yapilan ile devam ettirilir ilgili kapalilik ozellikleri saglanana kadar genisletilen altkumeler kumesidir Bu yapiya denir Motivasyons cebirleri icin en az uc temel motivasyon vardir olculerin tanimlanmasi kumelerin limitlerinin islenmesi ve kumelerle karakterize edilen kismi bilginin yonetilmesi Olcu Bir X kumesi uzerinde tanimli bir olcu X in altkumelerine sifir ya da pozitif bir gercel sayi atayan bir fonksiyondur Olcu kavrami kumeler icin buyukluk ya da hacim kavramlarinin matematiksel dil ve hassasiyet icinde tanimlanmasi olarak dusunulebilir Ayrik kumelerin birlesimlerinin olcusunun bu kumelerin olculerinin toplami olmasini istenir ki bu durum ayrik kumeler icin sonsuz dizilerde bile gecerli olmalidir X kumesinin her altkumesine bir olcu atamak istenebilir ancak bircok dogal durumda bu mumkun degildir Ornegin secim aksiyomu gercel dogru uzerindeki uzunluk kavrami altinda bazi kumelere olcu atamanin mumkun olmadigini soyler Bu duruma ornek olarak verilebilir Bu nedenle bunun yerine X in ayricalikli bir altkume ailesi olan daha kucuk bir kume ailesi dikkate alinir Bu ailedeki altkumelere olculebilir kumeler denir Olculebilir kumeler dogal olarak su islemler altinda kapalidir bir olculebilir kumenin tumleyeni yine olculebilir olmalidir ve olculebilir kumelerin sayilabilir birlesimi de olculebilir olmalidir Bu ozelliklere sahip bos olmayan kume koleksiyonlarina s cebiri denir Kumelerin limitleri Olcu kavraminin bircok kullaniminda ornegin olasiliktaki gibi durumlarda kumelerin dizilerinin limitleri onemlidir Bu tur limitler icin sayilabilir birlesimler ve kesisimler altinda kapali olma ozelligi cok onemlidir s cebirleri uzerinde kume limitleri su sekilde tanimlanir X displaystyle X teki A1 A2 A3 displaystyle A 1 A 2 A 3 ldots gibi altkumeler dizisi icin en kucuk ust limit ya da dis limit lim supn An n 1 m n Am n 1 An An 1 displaystyle limsup n to infty A n bigcap n 1 infty bigcup m n infty A m bigcap n 1 infty A n cup A n 1 cup cdots Bu limit bu kumelerin sonsuz tanesinde yer alan ya da esdeger olarak bunlarin bulunan tum noktalari icerir Yani bir x displaystyle x noktasi ancak ve ancak x An1 An2 displaystyle x in A n 1 cap A n 2 cap cdots olacak sekilde sonsuz bir An1 An2 displaystyle A n 1 A n 2 ldots altdizisi icerisinde yer aliyorsa x lim supn An displaystyle x in limsup n to infty A n olur Ayni dizi icin en buyuk alt limit ya da ic limit lim infn An n 1 m n Am n 1 An An 1 displaystyle liminf n to infty A n bigcup n 1 infty bigcap m n infty A m bigcup n 1 infty A n cap A n 1 cap cdots Bu limit yalnizca sonlu sayida kume haricindeki tum kumelerde bulunan veya esdeger sekilde sonlu bir asamadan itibaren tum kumelerde yer alan noktalari icerir Yani x lim infn An displaystyle x in liminf n to infty A n ancak ve ancak x AN AN 1 displaystyle x in A N cap A N 1 cap cdots olacak sekilde bir N N displaystyle N in mathbb N bulunuyorsa gecerlidir Her zaman lim infn An lim supn An displaystyle liminf n to infty A n subseteq limsup n to infty A n olur Eger bu iki limit esitse bu ortak kumeye limn An displaystyle lim n to infty A n limiti denir ve limn An lim infn An lim supn An displaystyle lim n to infty A n liminf n to infty A n limsup n to infty A n olur Alt s cebirler Olasiligin bircok kisminda ozellikle kosullu beklenti soz konusu oldugunda gozlemlenebilecek tum bilgilerin yalnizca bir kismini temsil eden kumeler dikkate alinir Bu kismi bilgi asil s cebirin bir altkumesi olan daha kucuk bir s cebiri ile tanimlanabilir bu alt s cebiri yalnizca kismi bilgiye gore belirlenebilen kumelerden olusur Bicimsel olarak S displaystyle Sigma ve S displaystyle Sigma kumesi X uzerinde tanimli s cebirler olsun Eger S S displaystyle Sigma subseteq Sigma ise S displaystyle Sigma kumesi S displaystyle Sigma nin bir alt s cebiridir Bu fikri aciklamak basit ornekler yararli olacaktir Iki kisinin yazi tura atarak oynadigi ve sonsuza dek surebilecek bir oyun oynadigini hayal edelim Her iki oyuncunun da sonsuz zengin oldugu varsayimi altinda oyuna suresiz bir sekilde devam edilebilir Bu durumda orneklem uzayi W sonsuz sayida yazi tura sonucunu temsil eden dizilerden olusur W H T x1 x2 x3 xi H T i 1 displaystyle Omega H T infty x 1 x 2 x 3 dots x i in H T i geq 1 Ilk n atistan sonra gozlemlenen bilgi ilk n yazi tura sonucunu aciklayan 2n displaystyle 2 n olasiliktan biridir Bu bilgi asagidaki alt s cebiriyle temsil edilir Gn A H T A H T n displaystyle mathcal G n A times H T infty A subseteq H T n Bu yapi ilk n yazi tura atisini sabitlemektedir ama kalan sonuclara dair herhangi bir bilgi icermemektedir Bu durumda G1 G2 G3 G displaystyle mathcal G 1 subseteq mathcal G 2 subseteq mathcal G 3 subseteq cdots subseteq mathcal G infty seklinde bir artan s cebiri dizisi elde edilir burada G displaystyle mathcal G infty digerlerinin tumunu iceren en kucuk s cebiridir Tanim ve ozelliklerTanim Bir X kumesi verilsin ve P X displaystyle P X ifadesi X in yani Xin tum altkumelerinin kumesini gostersin O halde S P X displaystyle Sigma subseteq P X alt kumesi ancak ve ancak asagidaki uc ozelligi sagliyorsa bir s cebiri olarak adlandirilir X S displaystyle X in Sigma olmalidir S displaystyle Sigma tumleyene gore kapalidir Eger A S displaystyle A in Sigma ise X A displaystyle X setminus A da S displaystyle Sigma icindedir S displaystyle Sigma sayilabilir birlesimlere gore kapalidir Eger A1 A2 A3 S displaystyle A 1 A 2 A 3 ldots in Sigma ise o halde A A1 A2 A3 displaystyle A A 1 cup A 2 cup A 3 cup cdots da S displaystyle Sigma icindedir Bu ozelliklerden s cebirinin ayni zamanda sayilabilir kesisimlere gore de kapali oldugu sonucu cikar ki bu durum De Morgan yasasi yardimiyla gosterilebilir Ayrica X S displaystyle X in Sigma oldugu icin ve 2 numarali ozellige gore tumleyeni olan bos kume displaystyle varnothing da S displaystyle Sigma icindedir Dahasi X displaystyle X varnothing kumesi bu uc kosulu da sagladigi icin X displaystyle X kumesi uzerindeki en kucuk s cebiridir Ote yandan P X displaystyle P X yani kuvvet kumesi en buyuk s cebiridir Bir s cebirin elemanlari olculebilir kumeler olarak adlandirilir X displaystyle X bir kume ve S displaystyle Sigma onun uzerinde bir s cebiri olmak uzere sirali ikili X S displaystyle X Sigma bir olculebilir uzay olarak adlandirilir Iki olculebilir uzay arasinda tanimli bir fonksiyon alindiginda eger goruntu kumesindeki her olculebilir kumenin de olculebilir ise bu fonksiyon olculebilir fonksiyon olarak adlandirilir Olculebilir uzaylarin olusturdugu aile bir kategori olusturur burada olculebilir fonksiyonlar Olculer ise bir s cebirinden 0 displaystyle 0 infty araligina tanimlanan belirli turde fonksiyonlardir Bir s cebiri hem bir hem de bir veya l sistemi Tersi de yine ne gore dogrudur Dynkin p l teoremi Bu teorem ya da iliskili olan belirli s cebirlerinin ozelliklerine dair bircok sonucun ispatinda kullanilan temel bir aractir Bu teorem iki daha basit kume sinifinin dogasini kullanir Bir P displaystyle P sonlu sayida kumenin kesisimi altinda kapali olan altkumeler kumesidir Bir ya da l sistemi D displaystyle D X displaystyle X kumesini iceren ve gore ve ayrik altkumelerin sayilabilir birlesimleri altinda kapali olan altkumeler kumesidir Dynkin p l teoremi ise sunu ifade eder eger P displaystyle P bir p sistemi ve D displaystyle D bir Dynkin sistemi olup P D displaystyle P subseteq D ise P displaystyle P tarafindan s cebiri s P displaystyle sigma P D displaystyle D kumesinin alt kumesidir s P D displaystyle sigma P subseteq D Bazi p sistemleri oldukca basit kume siniflarindan olustugu icin P displaystyle P icindeki tum kumelerin istenilen ozellige sahip oldugunu gostermek zor olmayabilir Ote yandan bu ozellige sahip tum kumelerden olusan D displaystyle D kumesinin bir Dynkin sistemi oldugunu gostermek de nispeten kolay olabilir Bu durumda Dynkin p l teoremi s P displaystyle sigma P icindeki tum kumelerin de bu ozellige sahip oldugunu garanti eder ve boylece s P displaystyle sigma P icindeki tum kumeleri ayri ayri kontrol etme geregini ortadan kaldirir Bu teoremin en temel kullanim alanlarindan biri ayri ayri tanimlanmis olculerin veya integrallerin esdegerligini gostermektir Ornegin bu teorem rasgele bir degisken X displaystyle X icin tanimlanan bir olasiligin ile ifade edilen karsiligina esitligini gostermek icin kullanilir A displaystyle A R displaystyle mathbb R uzerindeki Borel s cebirine ait olmak uzere her A displaystyle A icin P X A AF dx displaystyle mathbb P X in A int A F dx Burada F x displaystyle F x X displaystyle X icin tanimlanmis kumulatif dagilim fonksiyonudur ve P displaystyle mathbb P bir olup W displaystyle Omega orneklem uzayinin alt kumelerinden olusan bir s cebiri S displaystyle Sigma uzerinde tanimlidir s cebirlerinin birlestirilmesi Varsayalim ki Sa a A displaystyle left Sigma alpha alpha in mathcal A right bir X displaystyle X uzayi uzerinde tanimli s cebirlerinden olusan bir aile olsun Kesisim Bir s cebiri ailesinin kesisimi yine bir s cebiridir Bu ozellik vurgulanmak istendiginde su sekilde gosterilir a ASa displaystyle bigwedge alpha in mathcal A Sigma alpha Ispat taslagi S displaystyle Sigma ile bu kesisimi gosterelim Her Sa displaystyle Sigma alpha s cebiri oldugu icin X S displaystyle X in Sigma olur yani S displaystyle Sigma bos degildir Her Sa displaystyle Sigma alpha tumleyene ve sayilabilir birlesimlere gore kapali oldugu icin bu ozellikler S displaystyle Sigma icin de gecerlidir Dolayisiyla S displaystyle Sigma bir s cebiridir Birlesim s cebirlerinin birlesimi genel olarak ne bir s cebiridir ne de bir cebirdir ancak bu birlesim bir s cebiri Bu s cebire birlestirme join denir ve genellikle soyle gosterilir a ASa s a ASa displaystyle bigvee alpha in mathcal A Sigma alpha sigma left bigcup alpha in mathcal A Sigma alpha right Bu birlestirmeyi ureten bir su sekilde ifade edilir P i 1nAi Ai Sai ai A n 1 displaystyle mathcal P left bigcap i 1 n A i A i in Sigma alpha i alpha i in mathcal A n geq 1 right Ispat taslagi n 1 displaystyle n 1 durumu icin her Sa P displaystyle Sigma alpha subset mathcal P olur dolayisiyla a ASa P displaystyle bigcup alpha in mathcal A Sigma alpha subseteq mathcal P Bu durumdan s a ASa s P displaystyle sigma left bigcup alpha in mathcal A Sigma alpha right subseteq sigma mathcal P sonucu elde edilir cunku s displaystyle sigma cdot ifadesi bir altkume ailesi tarafindan olusturulan en kucuk s cebirini ifade eder Ote yandan P s a ASa displaystyle mathcal P subseteq sigma left bigcup alpha in mathcal A Sigma alpha right oldugundan uyarinca su sonuc elde edilir s P s a ASa displaystyle sigma mathcal P subseteq sigma left bigcup alpha in mathcal A Sigma alpha right Alt uzaylar icin s cebirleri X S displaystyle X Sigma bir olculebilir uzay ve Y displaystyle Y X displaystyle X kumesinin bir altkumesi olsun Y B B S displaystyle Y cap B B in Sigma ailesi Y displaystyle Y kumesinin altkumelerinden olusan bir s cebiridir Y L displaystyle Y Lambda olculebilir bir uzay olmak uzere A X A Y L displaystyle A subseteq X A cap Y in Lambda ailesi X displaystyle X kumesinin altkumelerinden olusan bir s cebiridir s halka ile iliskisi Bir s cebiri S displaystyle Sigma evrensel kume olan X displaystyle X kumesini iceren bir Her s cebiri ayni zamanda bir s halkadir ancak her s halka bir s cebiri olmak zorunda degildir Ornegin gercel dogru uzerindeki sifir sahip tum olculebilir kumeler bir s halka olusturur fakat bu kumeler gercel dogrunun tamamini kapsayamayacagi icin bir s cebiri olusturmazlar cunku gercel dogrunun olcusu sonsuzdur ve bu kumelerin sayilabilir birlesimiyle elde edilemez Buna karsilik sonlu olcuye sahip Lebesgue olculebilir kumelerin olusturdugu aile bir fakat bir s halka degildir cunku bu kumelerin sayilabilir birlesimi gercel dogruyu verebilir Ancak toplam olcu sonlu olmayabilir Tipografik not s cebirleri bazen buyuk harflerle veya gosterilir Bu nedenle X S displaystyle X Sigma ifadesi X F displaystyle scriptstyle X mathcal F ya da X F displaystyle scriptstyle X mathfrak F bicimlerinde de yazilabilir Onemli durumlar ve orneklerAyrilabilir s cebirler Bir ayrilabilir s cebiri ya da ayrilabilir s cismi ozelligi tasiyan ve sonlu bir m displaystyle mu olcusu ile birlikte her A B F displaystyle A B in mathcal F icin r A B m A B displaystyle rho A B mu A mathbin triangle B ozelligini saglayan bir r displaystyle rho metrigine sahip bir metrik uzay olarak dusunuldugunde elde edilen bir s cebiridir Sayilabilir bir kume ailesi tarafindan olusturulan her s cebiri ayrilabilirdir ancak bunun tersi dogru olmayabilir Ornegin ayrilabilirdir cunku her Lebesgue olculebilir kume bir ile olcu bakimindan esdegerdir fakat sayilabilir olarak uretilemez cunku kardinalitesi sureyden buyuktur Ayrilabilir bir olcu uzayi onu yapan dogal bir yapisina sahiptir Bu durumda iki kume arasindaki uzaklik bu kumelerin simetrik farkinin olcusune esittir Ancak simetrik farkin olcusu sifir olan farkli kumeler olabileceginden bu uzaklik bir gercek metrik olusturmaz Bununla birlikte olcusu sifir olan farklara sahip kumeleri bir olarak tanimlarsak olusan uzerinde gercek bir metrik tanimlanabilir Eger olcu uzayi ayrilabilirse elde edilen metrik uzayin da ayrilabilir oldugu gosterilebilir Basit kume temelli ornekler Herhangi bir X displaystyle X kumesi icin asagidaki s cebiri ornekleri verilebilir Yalnizca bos kume ve X displaystyle X kumesini iceren aile X displaystyle X uzerindeki en kucuk asikar s cebiridir X displaystyle varnothing X X displaystyle X kumesinin yani tum altkumelerinin kumesi ayrik s cebiri ya da tam s cebiri olarak adlandirilir A X A X displaystyle varnothing A X setminus A X ailesi A displaystyle A altkumesinin olusturdugu basit bir s cebiridir X displaystyle X kumesinin oldugu varsayilirsa X displaystyle X in sayilabilir olan ya da tumleyeni sayilabilir olan tum altkumelerinden olusan kume bir s cebiridir Bu s cebiri X displaystyle X in elemanlarinin olusturdugu s cebiridir Sayilabilir kavrami burada sonlu ya da bos kumeleri de icermektedir X displaystyle X in sayilabilir bir verilmisse bu bolmeyi olusturan kumelerin tum birlesimlerinden bos kume dahil olusan kume bir s cebiridir Durdurma zamani s cebirleri Bir t displaystyle tau durdurma zamani s cebiri olan Ft displaystyle mathcal F tau yi tanimlamak icin kullanilabilir Bu s cebiri bir suzgec yapisina sahip olasilik uzayinda rasgele bir zaman t displaystyle tau ya kadar elde edilebilecek bilgiyi ifade eder Yani bu yapi soyle yorumlanabilir Eger suzgecli olasilik uzayi bir rasgele deneme olarak dusunulurse bu deneme t displaystyle tau zamanina kadar sinirsiz sayida tekrarlandiginda ogrenilebilecek maksimum bilgi Ft displaystyle mathcal F tau ile temsil edilir Kume aileleri tarafindan olusturulan s cebirleriHerhangi bir kume ailesi tarafindan olusturulan s cebiri F displaystyle F herhangi bir altkume ailesi bir olsun yani F P X displaystyle F subseteq P X O halde F displaystyle F yi iceren tum s cebirlerinin kesisimi F displaystyle F yi iceren en kucuk s cebirini verir Bu s cebire s F displaystyle sigma F denir ve F displaystyle F tarafindan olusturulan s cebiri olarak adlandirilir Eger F displaystyle F bos kume ise s X displaystyle sigma varnothing varnothing X olur Bos olmayan durumlarda s F displaystyle sigma F F displaystyle F deki kumelerden baslayarak sayilabilir sayida birlesim ve kesisim islemleriyle elde edilebilen tum kumeleri icerir Basit bir ornek olarak X 1 2 3 displaystyle X 1 2 3 kumesi uzerinde yalnizca 1 displaystyle 1 kumesini iceren bir aile ele alalim Bu durumda s 1 1 2 3 1 2 3 displaystyle sigma 1 varnothing 1 2 3 1 2 3 olur acisindan yalnizca bir kumeden olusan F A displaystyle F A icin s A displaystyle sigma A ifadesi s A displaystyle sigma A yerine kullanilabilir Ayni sekilde s A1 A2 displaystyle sigma left A 1 A 2 ldots right yazimi da s A1 A2 displaystyle sigma left A 1 A 2 ldots right anlaminda sikca kullanilir Kullanisli bircok s cebiri farkli kumeler ailelerinden olusturulur Bazi yaygin ornekler asagida verilmistir Bir fonksiyon tarafindan olusturulan s cebiri Eger f displaystyle f X displaystyle X kumesinden Y displaystyle Y kumesine tanimli bir fonksiyon ve B displaystyle B Y displaystyle Y kumesi uzerinde tanimli bir s cebiri ise o zaman f displaystyle f fonksiyonu tarafindan olusturulan s cebiri soyle tanimlanir s f f 1 S S B displaystyle sigma f left f 1 S S in B right Yani s f displaystyle sigma f B displaystyle B deki tum kumelerin olsan kumedir Bu yapi X displaystyle X kumesi uzerinde bir s cebiridir Bir f displaystyle f fonksiyonu X S displaystyle X Sigma ile Y B displaystyle Y B arasinda tanimlanmissa ve s f S displaystyle sigma f subseteq Sigma ise o zaman f displaystyle f fonksiyonu olculebilir fonksiyon olarak adlandirilir En sik karsilasilan durum Y displaystyle Y kumesinin bir metrik uzay veya topolojik uzay oldugu ve B displaystyle B nin Y displaystyle Y uzerindeki oldugu durumlardir Ozellikle f displaystyle f fonksiyonu X Rn displaystyle X to mathbb R n bicimindeyse s f displaystyle sigma f genellikle Rn displaystyle mathbb R n icindeki aralik ya da kutularin ters goruntulerinden turetilen s cebiridir s f s f 1 a1 b1 an bn ai bi R displaystyle sigma f sigma left left f 1 a 1 b 1 times cdots times a n b n a i b i in mathbb R right right Yararli bir ozellik ise soyledir Varsayalim f displaystyle f X SX displaystyle X Sigma X den S SS displaystyle S Sigma S ye olculebilir bir fonksiyon ve g displaystyle g de X SX displaystyle X Sigma X den T ST displaystyle T Sigma T ye olculebilir bir fonksiyon olsun Eger f x h g x displaystyle f x h g x olacak sekilde h displaystyle h adinda T ST S SS displaystyle T Sigma T to S Sigma S biciminde bir olculebilir fonksiyon varsa o zaman s f s g displaystyle sigma f subseteq sigma g olur Ayrica S displaystyle S kumesi sonlu ya da sayilabilir ise veya daha genel olarak bir ise ornegin ayrilabilir ve tam bir metrik uzay bu durumda tersi ifade de gecerlidir Standart ornekler arasinda sunlar vardir Rn displaystyle mathbb R n uzerindeki Borel s cebiri R displaystyle mathbb R infty uzerindeki silindir s cebiri asagida tanimlanmistir Borel ve Lebesgue s cebirleri Onemli bir ornek herhangi bir topolojik uzay uzerindeki Borel cebiridir Bu acik kumeler ya da esdeger bicimde kapali kumeler tarafindan olusturulan s cebiridir Bu s cebir genellikle topolojik uzayin degildir Asikar olmayan kumelere ornek olarak veya verilebilir Rn displaystyle mathbb R n gibi bir Oklid uzayi uzerinde bir diger onemli s cebiri tum olusturdugu s cebiridir Bu s cebir Rn displaystyle mathbb R n uzerindeki Borel s cebirinden daha fazla kume icerir ve integral kurami acisindan daha uygundur cunku bir olcu uzayi saglar Carpim s cebiri X1 S1 displaystyle X 1 Sigma 1 ve X2 S2 displaystyle X 2 Sigma 2 iki olculebilir uzay olsun Bu durumda carpim uzayi X1 X2 displaystyle X 1 times X 2 uzerindeki s cebire carpim s cebiri ya da s cebir carpimi denir ve su sekilde tanimlanir S1 S2 s B1 B2 B1 S1 B2 S2 displaystyle Sigma 1 times Sigma 2 sigma left left B 1 times B 2 B 1 in Sigma 1 B 2 in Sigma 2 right right Buradaki B1 B2 B1 S1 B2 S2 displaystyle B 1 times B 2 B 1 in Sigma 1 B 2 in Sigma 2 koleksiyonu bir dolayisiyla bu kumelerden olusturulan s cebir en kucuk s cebiri olur Rn displaystyle mathbb R n uzerindeki asagidaki sekillerde uretilebilir B Rn s b1 bn bi R s a1 b1 an bn ai bi R displaystyle mathcal B mathbb R n sigma left left infty b 1 times cdots times infty b n b i in mathbb R right right sigma left left left a 1 b 1 right times cdots times left a n b n right a i b i in mathbb R right right Her iki durumda da kullanilan uretec kumeler ailesi bir p sistemidir Silindir kumeleri tarafindan olusturulan s cebiri Varsayalim ki X RT f f t R t T displaystyle X subseteq mathbb R mathbb T f f t in mathbb R t in mathbb T seklinde gercel degerli fonksiyonlardan olusan bir kume olsun B R displaystyle mathcal B mathbb R ise gercel sayilar uzerindeki gostersin X in bir silindir kumesi yalnizca sonlu sayida zaman noktasinda kisitlanan kumeler olarak tanimlanir Ct1 tn B1 Bn f X f ti Bi 1 i n displaystyle C t 1 dots t n B 1 dots B n left f in X f t i in B i 1 leq i leq n right Her Ct1 tn B1 Bn Bi B R 1 i n displaystyle left C t 1 dots t n B 1 dots B n B i in mathcal B mathbb R 1 leq i leq n right kume ailesi t1 tn displaystyle t 1 dots t n noktalari sabitlenmis olmak uzere bir p sistemi olusturur ve bunun urettigi s cebir soyle gosterilir St1 tn displaystyle Sigma t 1 dots t n Daha sonra bu p sistemlerinin tum zaman indeksleri ti T displaystyle t i in mathbb T uzerinden alinarak olusturdugu FX n 1 ti T i nSt1 tn displaystyle mathcal F X bigcup n 1 infty bigcup t i in mathbb T i leq n Sigma t 1 dots t n ailesi bir olusturur ve bu cebirin olusturdugu s cebir X displaystyle X kumesi uzerindeki silindir s cebiri olarak adlandirilir Bu s cebir RT displaystyle mathbb R mathbb T uzerindeki tarafindan belirlenen Borel s cebirinin bir altcebiridir Onemli bir ozel durum T N displaystyle mathbb T mathbb N dogal sayilar oldugunda yani X displaystyle X gercel degerli diziler kumesi oldugunda ortaya cikar Bu durumda silindir kumeleri asagidaki bicimi alir Cn B1 Bn B1 Bn R X x1 x2 X xi Bi 1 i n displaystyle C n B 1 dots B n left B 1 times cdots times B n times mathbb R infty right cap X left x 1 x 2 ldots in X x i in B i 1 leq i leq n right Bunlarin olusturdugu s cebir ise Sn s Cn B1 Bn Bi B R 1 i n displaystyle Sigma n sigma left left C n B 1 dots B n B i in mathcal B mathbb R 1 leq i leq n right right seklindedir ve bu s cebirler azalmayan bir dizi olusturur Yuvar s cebiri Yuvar s cebiri bir metrik uzayda tum acik veya kapali iceren en kucuk s cebiridir Bu s cebir hicbir zaman daha buyuk degildir Not edilmelidir ki ayrilabilir uzaylar icin Borel s cebiri ile yuvar s cebiri aynidir Ancak bazi bazi fonksiyonlar Borel olculebilir degildir ama yuvar s cebirine gore olculebilirdir Bu durum ozellikle boyle uzaylarda tanimli fonksiyonlarin analizi icin yuvar s cebirinin kullanilmasini degerli kilar Bir rasgele degisken veya vektor tarafindan olusturulan s cebiri Varsayalim ki W S P displaystyle Omega Sigma mathbb P bir olasilik uzayi olsun Eger Y W Rn displaystyle Y Omega to mathbb R n fonksiyonu Rn displaystyle mathbb R n uzerindeki gore olculebilir bir fonksiyon ise Y displaystyle Y bir rasgele degisken n 1 icin ya da rasgele vektor n gt 1 icin olarak adlandirilir Bu durumda Y displaystyle Y tarafindan olusturulan s cebiri sudur s Y Y 1 A A B Rn displaystyle sigma Y left Y 1 A A in mathcal B mathbb R n right Bir rasgele surec tarafindan olusturulan s cebiri Varsayalim ki W S P displaystyle Omega Sigma mathbb P bir olasilik uzayi ve RT displaystyle mathbb R mathbb T gercel degerli fonksiyonlarin olusturdugu kume olsun Eger Y W X RT displaystyle Y Omega to X subseteq mathbb R mathbb T fonksiyonu X displaystyle X kumesi uzerindeki s FX displaystyle sigma mathcal F X ye gore olculebilir ise o zaman Y displaystyle Y bir rasgele surec ya da stokastik surec olarak adlandirilir Bu durumda Y displaystyle Y tarafindan olusturulan s cebiri su sekilde tanimlanir s Y Y 1 A A s FX s Y 1 A A FX displaystyle sigma Y left Y 1 A A in sigma mathcal F X right sigma left left Y 1 A A in mathcal F X right right Ayrica bakinizOlculebilir fonksiyon Orneklem uzayiKaynakca Elstrodt J 2018 Mass Und Integrationstheorie Springer Spektrum Berlin Heidelberg https doi org 10 1007 978 3 662 57939 8 11 Olculebilir Uzaylar Random Probability Mathematical Statistics Stochastic Processes University of Alabama in Huntsville Department of Mathematical Sciences 30 Ocak 2022 tarihinde kaynagindan arsivlendi Erisim tarihi 30 Mart 2016 Bir s cebiri ayni zamanda bir cebirdir dolayisiyla cebirler icin gecerli temel sonuclar burada da gecerlidir 2012 Probability and Measure Anniversary Wiley ISBN 978 1 118 12237 2 1987 Real amp Complex Analysis McGraw Hill ISBN 0 07 054234 1 Vestrup Eric M 2009 The Theory of Measures and Integration John Wiley amp Sons s 12 ISBN 978 0 470 31795 2 Dzamonja Mirna 1995 Properties of the class of measure separable compact spaces PDF Fundamenta Mathematicae s 262 7 Mayis 2024 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 28 Mart 2025 Fischer Tom 2013 On simple representations of stopping times and stopping time sigma algebras Statistics and Probability Letters 83 1 ss 345 349 arXiv 1112 1603 2 doi 10 1016 j spl 2012 09 024 2001 Foundations of Modern Probability 2nd s 7 ISBN 0 387 95313 2 van der Vaart A W amp Wellner J A 1996 Weak Convergence and Empirical Processes In Springer Series in Statistics Springer New York https doi org 10 1007 978 1 4757 2545 2Dis baglantilarHazewinkel Michiel Ed 2001 Kumeler Cebiri Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Sigma Cebiri PlanetMath sitesinden
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State













