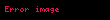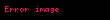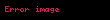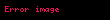Matematikte integral testi veya bir diğer deyişle yakınsaklık için integral testi, terimleri negatif olmayan sonsuz serilerin yakınsaklığını belirlemek için kullanılan bir yöntemdir. Bu testin erken bir versiyonu 14. yüzyılda Hint matematikçi Madhava ve takipçileri tarafından bulunmuştur. Avrupa'da ise Maclaurin ve Cauchy tarafından geliştirilmiş olup aynı zamanda Maclaurin-Cauchy testi olarak da bilinir.

Testin ifadesi
Bir N tam sayısını ve sınırsız [N, ∞) aralığında tanımlı monoton azalan bir f fonksiyonunu ele alalım. O zaman,
serisi ancak ve ancak
integrali sonlu ise, yakınsaktır. Özelde, integral ıraksar ise, o zaman seri de ıraksar.
İspat
İspat basit bir şekilde f(n) terimini f 'nin [n − 1, n] ve [n, n + 1] aralıkları üzerindeki integralleriyle karşılaştırarak, karşılaştırma testini kullanmaktadır
f, monoton azalan bir fonksiyon olduğu için,
ve
olduğunu biliyoruz. Bu yüzden, N 'den büyük n için,
Alt tahmin de aynı zamanda f(N) için geçerli olduğu için, N 'den belli bir M (M, N 'den büyüktür) tam sayısına kadar n üzerinden toplamlarla
elde ederiz. M sonsuza giderse, sonucu elde ederiz.
Uygulamalar
ıraksar çünkü doğal logaritmayı, türevini ve hesabın temel teoremini kullanarak
elde edilir.
Tersine,
serisi (Riemann zeta fonksiyonu ile karşılaştırınız) her ε > 0 için yakınsar çünkü
Yakınsaklık ve ıraksaklık arasındaki sınır çizgisi
Yukarıdaki harmonik serileri de içeren örnekler şu soruyu beraberinde getirir: Terimleri f(n) olan ve 1/n 'den daha hızlı bir şekilde 0'a doğru azalan; ancak, 1/n1+ε 'dan her ε > 0 için
bağlamında 0'a doğru daha yavaş azalan monoton bir seri var mı ve bu seri yine de ıraksar mı? Böyle bir seri bulunur bulunmaz, aynı soru 1/n 'nin yerini almış f(n) ile de sorulabilir vs. Bu yolla, ıraksaklık ve yakınsaklık arasındaki sınır çizgisini araştırmak mümkündür.
İntegral testini kullanarak, her k doğal sayısı için
serisinin hala ıraksadığı gösterilebilir (k = 1 için, ile karşılaştırınız.); ancak
serisi her ε > 0 için yakınsar. Burada, lnk doğal logaritmanın arka arkaya k kere bileşkesinin alınmasını göstermektedir:
Dahası, Nk bu k bileşkenin iyi tanımlı olduğu ve lnkNk ≥ 1 eşitsizliğini sağlayan en küçük doğal sayıyı gösterir; yani
İlk serinin ıraksaklığını integral testi ile görmek için, zincir kuralının arka arkaya kullanımının
verdiğini görmemiz gerekir. Bu yüzden
İkinci serinin yakınsaklığını görmek için, kuvvet serisi, zincir kuralı ve yukarıdaki sonucun
verdiğini görmeliyiz. Bu yüzden,
olur.
Kaynakça
- Knopp, Konrad, "Infinite Sequences and Series", Dover publications, Inc., New York, 1956. (&; 3.3)
- Whittaker, E. T., and Watson, G. N., A Course in Modern Analysis, 4. baskı, Cambridge University Press, 1963. (§ 4.43)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte integral testi veya bir diger deyisle yakinsaklik icin integral testi terimleri negatif olmayan sonsuz serilerin yakinsakligini belirlemek icin kullanilan bir yontemdir Bu testin erken bir versiyonu 14 yuzyilda Hint matematikci Madhava ve takipcileri tarafindan bulunmustur Avrupa da ise Maclaurin ve Cauchy tarafindan gelistirilmis olup ayni zamanda Maclaurin Cauchy testi olarak da bilinir Integral TestiTestin ifadesiBir N tam sayisini ve sinirsiz N araliginda tanimli monoton azalan bir f fonksiyonunu ele alalim O zaman n N f n displaystyle sum n N infty f n serisi ancak ve ancak N f x dx displaystyle int N infty f x dx integrali sonlu ise yakinsaktir Ozelde integral iraksar ise o zaman seri de iraksar IspatIspat basit bir sekilde f n terimini f nin n 1 n ve n n 1 araliklari uzerindeki integralleriyle karsilastirarak karsilastirma testini kullanmaktadir f monoton azalan bir fonksiyon oldugu icin f x f n x n displaystyle f x leq f n quad text x in n infty ve f n f x x N n displaystyle f n leq f x quad text x in N n oldugunu biliyoruz Bu yuzden N den buyuk n icin nn 1f x dx nn 1f n dx f n n 1nf n dx n 1nf x dx displaystyle int n n 1 f x dx leq int n n 1 f n dx f n int n 1 n f n dx leq int n 1 n f x dx Alt tahmin de ayni zamanda f N icin gecerli oldugu icin N den belli bir M M N den buyuktur tam sayisina kadar n uzerinden toplamlarla NM 1f x dx n NMf n f N NMf x dx displaystyle int N M 1 f x dx leq sum n N M f n leq f N int N M f x dx elde ederiz M sonsuza giderse sonucu elde ederiz Uygulamalar n 1 1n displaystyle sum n 1 infty frac 1 n iraksar cunku dogal logaritmayi turevini ve hesabin temel teoremini kullanarak 1M1xdx ln x 1M ln M M iken displaystyle int 1 M frac 1 x dx ln x Bigr 1 M ln M to infty text quad M to infty quad text iken elde edilir Tersine n 1 1n1 e displaystyle sum n 1 infty frac 1 n 1 varepsilon serisi Riemann zeta fonksiyonu ile karsilastiriniz her e gt 0 icin yakinsar cunku 1M1x1 edx 1exe 1M 1e 1 1Me 1e M 1 displaystyle int 1 M frac 1 x 1 varepsilon dx frac 1 varepsilon x varepsilon biggr 1 M frac 1 varepsilon Bigl 1 frac 1 M varepsilon Bigr leq frac 1 varepsilon text quad forall M geq 1 Yakinsaklik ve iraksaklik arasindaki sinir cizgisiYukaridaki harmonik serileri de iceren ornekler su soruyu beraberinde getirir Terimleri f n olan ve 1 n den daha hizli bir sekilde 0 a dogru azalan ancak 1 n1 e dan her e gt 0 icin limn f n 1 n 0velimn f n 1 n1 e displaystyle lim n to infty frac f n 1 n 0 quad text ve quad lim n to infty frac f n 1 n 1 varepsilon infty baglaminda 0 a dogru daha yavas azalan monoton bir seri var mi ve bu seri yine de iraksar mi Boyle bir seri bulunur bulunmaz ayni soru 1 n nin yerini almis f n ile de sorulabilir vs Bu yolla iraksaklik ve yakinsaklik arasindaki sinir cizgisini arastirmak mumkundur Integral testini kullanarak her k dogal sayisi icin n Nk 1nln n ln2 n lnk 1 n lnk n displaystyle sum n N k infty frac 1 n ln n ln 2 n cdots ln k 1 n ln k n serisinin hala iraksadigi gosterilebilir k 1 icin ile karsilastiriniz ancak n Nk 1nln n ln2 n lnk 1 n lnk n 1 e displaystyle sum n N k infty frac 1 n ln n ln 2 n cdots ln k 1 n ln k n 1 varepsilon serisi her e gt 0 icin yakinsar Burada lnk dogal logaritmanin arka arkaya k kere bileskesinin alinmasini gostermektedir lnk x ln x k 1 ln lnk 1 x k 2 displaystyle ln k x begin cases ln x amp text k 1 ln ln k 1 x amp text k geq 2 end cases Dahasi Nk bu k bileskenin iyi tanimli oldugu ve lnkNk 1 esitsizligini saglayan en kucuk dogal sayiyi gosterir yani Nk ee e k tane e e k displaystyle N k geq underbrace e e cdot cdot e k text tane e e uparrow uparrow k Ilk serinin iraksakligini integral testi ile gormek icin zincir kuralinin arka arkaya kullaniminin ddxlnk 1 x ddxln lnk x 1lnk x ddxlnk x 1xln x lnk x displaystyle frac d dx ln k 1 x frac d dx ln ln k x frac 1 ln k x frac d dx ln k x cdots frac 1 x ln x cdots ln k x verdigini gormemiz gerekir Bu yuzden Nk dxxln x lnk x lnk 1 x Nk displaystyle int N k infty frac dx x ln x cdots ln k x ln k 1 x bigr N k infty infty Ikinci serinin yakinsakligini gormek icin kuvvet serisi zincir kurali ve yukaridaki sonucun ddx1e lnk x e 1 lnk x 1 eddxlnk x 1xln x lnk 1 x lnk x 1 e displaystyle frac d dx frac 1 varepsilon ln k x varepsilon frac 1 ln k x 1 varepsilon frac d dx ln k x cdots frac 1 x ln x cdots ln k 1 x ln k x 1 varepsilon verdigini gormeliyiz Bu yuzden Nk dxxln x lnk 1 x lnk x 1 e 1e lnk x e Nk lt displaystyle int N k infty frac dx x ln x cdots ln k 1 x ln k x 1 varepsilon frac 1 varepsilon ln k x varepsilon biggr N k infty lt infty olur KaynakcaKnopp Konrad Infinite Sequences and Series Dover publications Inc New York 1956 amp 3 3 ISBN 0 486 60153 6 Whittaker E T and Watson G N A Course in Modern Analysis 4 baski Cambridge University Press 1963 4 43 ISBN 0 521 58807 3
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State