Vektör fonksiyonu

Vektör değerli fonksiyon ya da vektör fonksiyonu, bir ya da daha fazla değişkeni sonlu ya da sonsuz boyutlu vektör olan fonksiyondur. Bir vektör fonksiyonunun girdisi skaler ya da vektör olabilir (yani girdi boyutu 1 ya da daha fazla olabilir). Fonksiyonun tanım kümesi ve değer kümesi farklı cinste olabilir.

Örnek

r(z) = ⟨2 cos z, 4 sin z, z⟩ fonksiyonunun z = 19.5 noktası yakınındaki (6π ve 6.5π arasında) değerleri

Vektör-değerli fonksiyonların yaygın örnekleri tek bir reel değişkene bağlı (t, örn. zaman), bir v(t) vektör değeri çıkaran fonksiyonlardır. Örneğin 3-boyutlu Kartezyen uzayda tanımlı (i, j, k taban vektörleriyle) bir vektör fonksiyonu aşağıdaki gibi gösterilebilir:

${\displaystyle \mathbf {v} (t)=f(t)\mathbf {i} +g(t)\mathbf {j} +h(t)\mathbf {k} }$

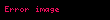
burada f(t), g(t) ve h(t) t parametresine bağlı koordinat fonksiyonlarıdır. v(t) vektör fonksiyonunun tanım kümesi bu üç fonksiyonun (f, g, h) tanım kümelerinin kesişimidir. Farklı bir gösterimi şu şekildedir:

${\displaystyle \mathbf {v} (t)=\langle f(t),g(t),h(t)\rangle }$

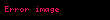
Bu fonksiyonun ürettiği v(t) vektörünün kuyruğu sıfır noktasında, kafası da fonksiyonun çıktısı olan noktadadır.

Örnek olarak, sağdaki görsel, r(z) = ⟨2 cos z, 4 sin z, z⟩ fonksiyonunun z = 19.5 noktası yakınındaki (6π ve 6.5π arasında) değerlerini göstermektedir. Bu fonksiyon bir şekli üretir.

Kaynakça

1. ^ Weisstein, Eric W. . mathworld.wolfram.com (İngilizce). 28 Mayıs 2000 tarihinde kaynağından arşivlendi. 
2. ^ . tutorial.math.lamar.edu. 17 Ağustos 2007 tarihinde kaynağından arşivlendi.