Matematiğin bir dalı olan çok değişkenli karmaşık analizde, Reinhardt bölgesi, içindeki noktaların üzerinden geçen 0 merkezli bütün çemberleri içeren özel bölgelerdir. Bu bölge, adını Alman matematikçi Karl Reinhardt'tan almaktadır.
Tanımı
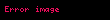




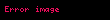


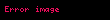
Örnekler
-boyutlu ve
vektör yarıçaplı Polidisk
-boyutlu,
merkezli ve
yarıçaplı yuvar
Logaritmik dışbükeylik
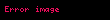

gönderimi altında



Yakınsaklık bölgesi
Bir karmaşık değişkenli karmaşık analizde yakınsaklık bölgesi ya disk olur ya da karmaşık düzlem olur. Bu bakış açısıyla, yüksek boyutlarda yakınsaklık bölgesi sadece yuvar ya da çoklu disk (polidisk) veya karmaşık koordinat uzayının tamamı değildir. Yüksek boyutlarda, kuvvet serilerinin yakınsaklık bölgesi tam Reinhardt bölgesi olmak zorundadır. Ancak, her tam Reinhardt bölgesi aynı zamanda bir kuvvet serisinin yakınsaklık bölgesi olmak zorunda değildir. Bunun için bu bölgelere geometrik özellikler getirmek zorunluluğu vardır. Daha açık bir şekilde yazmak gerekirse, bir Reinhardt bölgesinin bir kuvvet serisinin yakınsaklık bölgesi olması için gerekli ve yeterli özellik bu Reinhardt bölgesinin logaritmik dışbükey olmasıdır. Bu yüzden, Reinhardt bölgeleri, kuvvet veya Laurent serilerinin doğal tanım bölgeleridir denilebilir.
Thullen sınıflandırması
Peter Thullen'in 1931 yılındaki çalışması ile 
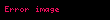


(polidisk);
();
(~Kompleks elipsoit).
- Otomorfi grubuna göre orijinin yörüngesinin yine orijin olduğu bölgeler. Diğer deyişle,
otomorfi grubuysa ve
de bu grubun birim elemanını içeren bağlantılı bileşense, o zaman
olan bölgeler.
Thullen, ayrıca, 

şeklinde tanımlı ve 






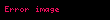
Kaynakça
- ^ Yakınsaklık tanımından yola çıkılırsa, yakınsaklık kümeleri boş küme ya da nokta da olabilir ama burada bahsediliyor.
- ^ Thullen, Peter (1931). "Zu den Abbildungen durch analytische Funktionen mehrerer komplexer Veränderlichen die Invarianz des Mittelpunktes von Kreiskörpern". Mathematische Annalen. Cilt 104. ss. 244-259. doi:10.1007/bf01457933.
- ^ Burada,
işleminden kasıt orijinin
-.
- ^ Burada,
, endeks permütasyonuna karşılık gelmektedir.
- ^ Sunada, Toshikazu (1978). "Holomorphic equivalence problem for bounded Reinhardt domains". Mathematische Annalen. 235 (2): 111-128. doi:10.1007/BF01405009.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir dali olan cok degiskenli karmasik analizde Reinhardt bolgesi icindeki noktalarin uzerinden gecen 0 merkezli butun cemberleri iceren ozel bolgelerdir Bu bolge adini Alman matematikci Karl Reinhardt tan almaktadir TanimiW Cn displaystyle Omega subset mathbb C n bir bolge olsun Her z z1 z2 zn W displaystyle z z 1 z 2 dots z n in Omega ve her ϑ1 ϑ2 ϑn R displaystyle vartheta 1 vartheta 2 dots vartheta n in mathbb R icin eiϑ1 z1 eiϑ2 z2 eiϑn zn W displaystyle left e i vartheta 1 cdot z 1 e i vartheta 2 cdot z 2 dots e i vartheta n cdot z n right in Omega ozelligi saglaniyorsa W displaystyle Omega ya Reinhardt bolgesi adi verilir W Cn displaystyle Omega subset mathbb C n bir Reinhardt bolgesi olsun Her z z1 z2 zn W C n displaystyle z z 1 z 2 dots z n in Omega cap mathbb C n icin w w1 w2 wn Cn wj lt zj W displaystyle left w w 1 w 2 dots w n in mathbb C n left w j right lt left z j right right subset Omega ozelligi saglaniyorsa o zaman W Cn displaystyle Omega subset mathbb C n ya tam Reinhardt bolgesi adi verilir Ornekler n displaystyle n boyutlu ve r1 r2 rn displaystyle rho 1 rho 2 dots rho n vektor yaricapli Polidisk z z1 z2 zn Cn zj lt rj j 1 2 n displaystyle left z z 1 z 2 dots z n in mathbb C n left z j right lt rho j j 1 2 dots n right n displaystyle n boyutlu 0 0 0 0 Cn displaystyle 0 0 0 dots 0 in mathbb C n merkezli ve r gt 0 displaystyle rho gt 0 yaricapli yuvar z z1 z2 zn Cn z1 2 z2 2 zn 2 lt r2 displaystyle left z z 1 z 2 dots z n in mathbb C n left z 1 right 2 left z 2 right 2 dots left z n right 2 lt rho 2 right Logaritmik disbukeylikW Cn displaystyle Omega subset mathbb C n bir Reinhardt bolgesi olsun ve W z z1 zn W z1 zn 0 displaystyle Omega z z 1 cdots z n in Omega z 1 cdots z n neq 0 tanimlansin l z l z ln z1 ln zn displaystyle lambda z rightarrow lambda z ln z 1 cdots ln z n gonderimi altinda l W displaystyle lambda Omega Rn displaystyle mathbb R n nin disbukey bir altkumesi oluyorsa W displaystyle Omega ya logaritmik disbukey denir Yakinsaklik bolgesi Bir karmasik degiskenli karmasik analizde yakinsaklik bolgesi ya disk olur ya da karmasik duzlem olur Bu bakis acisiyla yuksek boyutlarda yakinsaklik bolgesi sadece yuvar ya da coklu disk polidisk veya karmasik koordinat uzayinin tamami degildir Yuksek boyutlarda kuvvet serilerinin yakinsaklik bolgesi tam Reinhardt bolgesi olmak zorundadir Ancak her tam Reinhardt bolgesi ayni zamanda bir kuvvet serisinin yakinsaklik bolgesi olmak zorunda degildir Bunun icin bu bolgelere geometrik ozellikler getirmek zorunlulugu vardir Daha acik bir sekilde yazmak gerekirse bir Reinhardt bolgesinin bir kuvvet serisinin yakinsaklik bolgesi olmasi icin gerekli ve yeterli ozellik bu Reinhardt bolgesinin logaritmik disbukey olmasidir Bu yuzden Reinhardt bolgeleri kuvvet veya Laurent serilerinin dogal tanim bolgeleridir denilebilir Thullen siniflandirmasiPeter Thullen in 1931 yilindaki calismasi ile C2 displaystyle mathbb C 2 deki sinirli Reinhardt bolgeleri siniflandirilmistir Daha acik bir ifade ile yazmak gerekirse W C2 displaystyle Omega subset mathbb C 2 sinirli bir Reinhardt bolgesi ve 0 W displaystyle 0 in Omega olsun O zaman W displaystyle Omega asagidaki bolgelerden birine z w C2 z lt 1 w lt 1 displaystyle z w in mathbb C 2 z lt 1 w lt 1 polidisk z w C2 z 2 w 2 lt 1 displaystyle z w in mathbb C 2 z 2 w 2 lt 1 z w C2 z 2 w 2p lt 1 p gt 0 1 displaystyle z w in mathbb C 2 z 2 w frac 2 p lt 1 p gt 0 neq 1 Kompleks elipsoit Otomorfi grubuna gore orijinin yorungesinin yine orijin oldugu bolgeler Diger deyisle Aut D displaystyle Aut D otomorfi grubuysa ve G D displaystyle G D de bu grubun birim elemanini iceren baglantili bilesense o zaman G D 0 0 displaystyle G D cdot 0 0 olan bolgeler Thullen ayrica D1 displaystyle D 1 ve D2 displaystyle D 2 ile gosterilen sinirli Reinhardt bolgelerinin birbirine holomorf olarak denk olmalarinin ancak ve ancak z r1zw r2w veya z r3ww r4z ri gt 0 i 1 2 3 4 displaystyle begin cases z mapsto r 1 z w mapsto r 2 w end cases quad text veya quad begin cases z mapsto r 3 w w mapsto r 4 z end cases quad r i gt 0 i 1 2 3 4 seklinde tanimli ve D1 ϕ D2 displaystyle D 1 phi D 2 ozelligini saglayan bir ϕ displaystyle phi gonderiminin varligiyla mumkun olacagini kanitlamistir Toshikazu Sunada 1978 de Thullen in sonuclarinin bir genellemesini kanitlamistir Yani n displaystyle n boyutlu uzayda sinirli iki Reinhardt bolgesinin G1 displaystyle G 1 ve G2 displaystyle G 2 olsunlar birbirine biholomorf denk olmalarinin ancak ve ancak bu bolgelerin arasinda zi rizs i ri gt 0 displaystyle z i mapsto r i z sigma i r i gt 0 seklinde tanimli ve G1 f G2 displaystyle G 1 varphi G 2 ozelligini saglayan bir f Cn Cn displaystyle varphi mathbf C n longrightarrow mathbf C n gonderiminin varligiyla mumkun olacagini kanitlamistir Kaynakca Yakinsaklik tanimindan yola cikilirsa yakinsaklik kumeleri bos kume ya da nokta da olabilir ama burada bahsediliyor Thullen Peter 1931 Zu den Abbildungen durch analytische Funktionen mehrerer komplexer Veranderlichen die Invarianz des Mittelpunktes von Kreiskorpern Mathematische Annalen Cilt 104 ss 244 259 doi 10 1007 bf01457933 Burada G D 0 displaystyle G D cdot 0 isleminden kasit orijinin G D displaystyle G D Burada s displaystyle sigma endeks permutasyonuna karsilik gelmektedir Sunada Toshikazu 1978 Holomorphic equivalence problem for bounded Reinhardt domains Mathematische Annalen 235 2 111 128 doi 10 1007 BF01405009
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State














