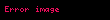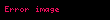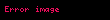Matematiğin bir kolu olan, fonksiyonlar teorisinde bir polidisk disklerin .
Daha ayrıntılı olarak, karmaşık düzlemde z noktası merkezli ve r yarıçaplı açık disk ile gösterilirse, o zaman açık polidisk aşağıdaki forma sahip bir kümedir:
Dengi bir ifade ise
olarak yazılabilir.
Polidisk, Cn'deki
olarak tanımlanan ile karıştırılmamalıdır.
Burada norm, Cn'deki Öklid uzaklığıdır.
olduğunda, açık yuvarlar ve açık polidiskler biholomorf olarak denk değildir, yani ikisi arasında yoktur. Bu sonuç 1907'de Poincaré tarafından ikisinin otomorfizm grubunun Lie grubu olarak değişik boyutlara sahip olduğu gösterilerek kanıtlanmıştır.
olduğunda ise bazen bidisk terimi kullanılır.
Kaynakça
- Steven G Krantz, Function Theory of Several Complex Variables, American Mathematical Society, 2002, .
- John P D'Angelo, D'Angelo P D'Angelo, Several Complex Variables and the Geometry of Real Hypersurfaces, CRC Press, 1993, .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir kolu olan fonksiyonlar teorisinde bir polidisk disklerin Daha ayrintili olarak karmasik duzlemde z noktasi merkezli ve r yaricapli acik disk D z r displaystyle D z r ile gosterilirse o zaman acik polidisk asagidaki forma sahip bir kumedir D z1 r1 D zn rn displaystyle D z 1 r 1 times dots times D z n r n Dengi bir ifade ise w w1 w2 wn Cn zk wk lt rk k 1 n displaystyle w w 1 w 2 dots w n in mathbf C n mid vert z k w k vert lt r k forall k 1 dots n olarak yazilabilir Polidisk Cn deki w Cn z w lt r displaystyle w in mathbf C n mid lVert z w rVert lt r olarak tanimlanan ile karistirilmamalidir Burada norm Cn deki Oklid uzakligidir n gt 1 displaystyle n gt 1 oldugunda acik yuvarlar ve acik polidiskler biholomorf olarak denk degildir yani ikisi arasinda yoktur Bu sonuc 1907 de Poincare tarafindan ikisinin otomorfizm grubunun Lie grubu olarak degisik boyutlara sahip oldugu gosterilerek kanitlanmistir n 2 displaystyle n 2 oldugunda ise bazen bidisk terimi kullanilir KaynakcaSteven G Krantz Function Theory of Several Complex Variables American Mathematical Society 2002 ISBN 0 8218 2724 3 John P D Angelo D Angelo P D Angelo Several Complex Variables and the Geometry of Real Hypersurfaces CRC Press 1993 ISBN 0 8493 8272 6
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State