Olasılık kuramı ve istatistik bilim dallarında bir rassal değişken X için olasılık yoğunluk fonksiyonu bir reel sayılı sürekli fonksiyonu olup f ile ifade edilir ve şu özellikleri olması gereklidir:
- üzerinde pozitif veya sıfır değerleri alır;
- üzerinde integral değeri bulunabilir;
- koşuluna uyar, yani eğri altındaki tüm alan bire eşittir.
Xin a ve b değerleri arasındaki olasılık, yani şu ifade kullanılarak hesaplanır:
Yani olasılık değeri f(x) integralini f(x) fonksiyonunu X=a ve X=b değerleri arasında entegrasyonu ile elde edilir.
Örneğin: X rassal değişkeninin [4.3,7.8] aralığında olasılık şöyle bulunur:
Ayrık dağılım ile sürekli dağılım arasındaki bağlantı
Bu maddenin başlangıcında verilmiş olasılık yoğunluk fonksiyonu tanımın bir sürekli dağılım ile ilişkili değişkenin [a; b] aralığı ile ilişkili çift-değerli ayrık değişkenler seti kullanılarak yapılmıştır.
Diğer bazı aralıklı rassal değişkenleri temsili, Dirac delta fonksiyonu aracılığı ile olasılığın yoğunluğun bulunması suretiyle de yapılabilir. Örneğin, bir çift-değerli her biri ½ olasılığı olan -1 ve 1 değerli bir rassal değişken ele alınsın. Bu değişkenle ilişkili olasılık yoğunluğu şöyle verilir:
Daha genel olarak, eğer bir ayrık değişken reel sayılar arasından 'n' tane değişik değer alınsın; o halde bunlarla ilişkili olasılık yoğunluk fonksiyonu şudur:
Burada 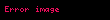
Bu ifade bir ayrık değişken için istatistiksel özellikleri (örneğin ortalama, varyans, çarpıklık, basıklık) sürekli dağılım için geliştirilmiş formülleri kullanarak hesaba başlayarak sonuçların bulunmasını sağlar.
Matematiksel olmayan olasılık yoğunluk tanımı
Bir olasılık dağılımı için yoğunluk fonksiyonu ancak ve ancak yığmalı dağılım fonksiyonu F(x) gösteriyorsa mümkündür. Bu halde F için türev bulunabilir ve F için alınan birinci türev olasılık ile yoğunluk şöyle bulunur:
Eğer bir olasılık dağılım için yoğunluk bulunması mümkün ise rassal değişken için her bir nokta değer (a) için olasılık 0 olacaktır.
Her olasılık dağılımı için bir yoğunluk fonksiyonu bulunamaz. Başta için olasılık yoğunluk fonksiyonu yoktur. Hiçbir noktaya pozitif olasılık vermeyen, yani hiç aralık parçası olmayan için de yoğunluk fonksiyonu bulunmaz.
Bir yığmalı dağılım fonksiyonunun türevi ile olasılık yoğunluk fonksiyonu arasındaki ilişkinin karmaşık matematik biçimlerden biraz aranmış açıklaması istatistiksel fizik dalında geliştirilmiştir ve bu genellikle olasılık yoğunluk fonksiyonu tanımı olarak kullanılabilir. Bu tanım şöyle yapılır:
dt sonsuz derece küçük bir sayı olarak alınsın. 
Moment, beklenen değer ve varyans
Sürekli X rassal değişkeni için ninci momenti E(Xn) gösterilip şu ifade ile verilir:
Beklenen değer o zaman birinci moment olup şöyle verilir:
Varyans ise şöyle verilir:
Bu ifade açılırsa
olur.
Çoklu değişkenlerle ilişkili olasılık fonksiyonu
Sürekli rassal değişkenler olan 

i=1, 2, …,n için tek bir değişken 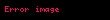
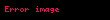

Bağımsızlık
Sürekli rassal değişken olan 
koşuluna tam olarak uymaları gerekir.
Eğer n elemanlı bir rassal değişken vektörünün ortak olasılık dağılımı tek bir değişken için n değişik fonksiyona faktörize edilebilirse; yani
ise, o halde, n değişkenin hepsi birbirlerinden bağımsızlık gösteriyor demektir. Bu halde her bir fonksiyon için marjinal olasılık yoğunluk fonksiyonu şöyle verilir:
Örneğin
Çoklu boyutlu olasılık yoğunluk fonksiyonlarının verilen tanımını biraz daha açığa kavuşturmak için basit bir örneğin alınsın; bu iki bilinmeyenli bir rassal vektör olsun. Koordinatları 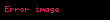


olur.
Kaynakça
- de Laplace, Pierre Simon (1812). Théorie Analytique des Probabilités.
- fr: İlk defa olasılık kuramı ile değişkenler hesabını bileştiren temel eser.
- Kolmogorov, Andrei Nikolajevich (1933). Grundbegriffe der Wahrscheinlichkeitrechnung.
- de:Olasılık kuramının ilk defa modern ölçü-teorisi temeline konulması. İngilizce tercümesi Foundations of the Theory of Probability olarak 1950de yayınlanmıştır.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami ve istatistik bilim dallarinda bir rassal degisken X icin olasilik yogunluk fonksiyonu bir reel sayili surekli fonksiyonu olup f ile ifade edilir ve su ozellikleri olmasi gereklidir R displaystyle mathbb R uzerinde pozitif veya sifir degerleri alir R displaystyle mathbb R uzerinde integral degeri bulunabilir Rf x dx 1 displaystyle int mathbb R f x dx 1 kosuluna uyar yani egri altindaki tum alan bire esittir Xin a ve b degerleri arasindaki olasilik yani P a lt X b displaystyle P a lt X leq b su ifade kullanilarak hesaplanir P a lt X b abf x dx displaystyle P left a lt X leq b right int a b f left x right dx Yani olasilik degeri f x integralini P a lt X lt b displaystyle P a lt X lt b f x fonksiyonunu X a ve X b degerleri arasinda entegrasyonu ile elde edilir Ornegin X rassal degiskeninin 4 3 7 8 araliginda olasilik soyle bulunur Pr 4 3 X 7 8 4 37 8f x dx displaystyle Pr 4 3 leq X leq 7 8 int 4 3 7 8 f x dx Ayrik dagilim ile surekli dagilim arasindaki baglantiBu maddenin baslangicinda verilmis olasilik yogunluk fonksiyonu tanimin bir surekli dagilim ile iliskili degiskenin a b araligi ile iliskili cift degerli ayrik degiskenler seti kullanilarak yapilmistir Diger bazi aralikli rassal degiskenleri temsili Dirac delta fonksiyonu araciligi ile olasiligin yogunlugun bulunmasi suretiyle de yapilabilir Ornegin bir cift degerli her biri olasiligi olan 1 ve 1 degerli bir rassal degisken ele alinsin Bu degiskenle iliskili olasilik yogunlugu soyle verilir f t 12 d t 1 d t 1 displaystyle f t frac 1 2 delta t 1 delta t 1 Daha genel olarak eger bir ayrik degisken reel sayilar arasindan n tane degisik deger alinsin o halde bunlarla iliskili olasilik yogunluk fonksiyonu sudur f t i 1nPid t xi displaystyle f t sum i 1 n P i delta t x i Burada x1 xn displaystyle x 1 ldots x n degisken ait degerler olur ve P1 Pn displaystyle P 1 ldots P n bu degerlerle iliskili olasiliklardir Bu ifade bir ayrik degisken icin istatistiksel ozellikleri ornegin ortalama varyans carpiklik basiklik surekli dagilim icin gelistirilmis formulleri kullanarak hesaba baslayarak sonuclarin bulunmasini saglar Matematiksel olmayan olasilik yogunluk tanimiBir olasilik dagilimi icin yogunluk fonksiyonu ancak ve ancak yigmali dagilim fonksiyonu F x gosteriyorsa mumkundur Bu halde F icin turev bulunabilir ve F icin alinan birinci turev olasilik ile yogunluk soyle bulunur ddxF x f x displaystyle frac d dx F x f x Eger bir olasilik dagilim icin yogunluk bulunmasi mumkun ise rassal degisken icin her bir nokta deger a icin olasilik 0 olacaktir Her olasilik dagilimi icin bir yogunluk fonksiyonu bulunamaz Basta icin olasilik yogunluk fonksiyonu yoktur Hicbir noktaya pozitif olasilik vermeyen yani hic aralik parcasi olmayan icin de yogunluk fonksiyonu bulunmaz Bir yigmali dagilim fonksiyonunun turevi ile olasilik yogunluk fonksiyonu arasindaki iliskinin karmasik matematik bicimlerden biraz aranmis aciklamasi istatistiksel fizik dalinda gelistirilmistir ve bu genellikle olasilik yogunluk fonksiyonu tanimi olarak kullanilabilir Bu tanim soyle yapilir dt sonsuz derece kucuk bir sayi olarak alinsin X displaystyle X in t t dt araliginda bulunacagi f t dt displaystyle f t dt ifadesine esittir yani Pr t lt X lt t dt f t dt displaystyle Pr t lt X lt t dt f t dt Moment beklenen deger ve varyansSurekli X rassal degiskeni icin ninci momenti E Xn gosterilip su ifade ile verilir E Xn xnfX x dx displaystyle E X n int infty infty x n f X x dx Beklenen deger o zaman birinci moment olup soyle verilir E X x f x dx displaystyle E left X right int infty infty x f x dx Varyans ise soyle verilir var X E X E X 2 x E X 2fX x dx displaystyle operatorname var X E X E X 2 int infty infty x E X 2 f X x dx Bu ifade acilirsa V X E X2 E X 2 displaystyle V left X right E left X 2 right left E left X right right 2 olur Coklu degiskenlerle iliskili olasilik fonksiyonuSurekli rassal degiskenler olan X1 Xn displaystyle X 1 ldots X n icin bu degiskenlerinin tumunu kapsayan icin bir olasilik yogunluk fonksiyonu tanimlamak mumkundur Buna ortak olasilik yogunluk fonksiyonu adi verilir n degiskenli bu yogunluk fonksiyonu matematik notasyon bicimleriyle soyle tanimlanir X1 Xn displaystyle X 1 ldots X n degiskenlerin degerleriyle tanimlanan n boyutlu uzayda bulunan herhangi bir D sahasi alinsin bu degisken setinin D sahasi icine dusen bir realizasyonun bulunacaginin olasiligi soyle verilir Pr X1 XN D DfX1 Xn x1 xN dx1 dxN displaystyle Pr left X 1 ldots X N in D right int D f X 1 dots X n x 1 ldots x N dx 1 cdots dx N i 1 2 n icin tek bir degisken Xi displaystyle X i ile iliskili olasilik yogunluk fonksiyonu fXi xi displaystyle f X i x i olarak ifade edilsin Bu olasilik yogunlugu X1 Xn displaystyle X 1 ldots X n rassal degiskenlerle iliskili olasilik yogunluklarindan n 1 tane diger degiskenlerle entegrasyonu suretiyle elde edilir fXi xi f x1 xn dx1 dxi 1dxi 1 dxn displaystyle f X i x i int f x 1 ldots x n dx 1 cdots dx i 1 dx i 1 cdots dx n Bagimsizlik Surekli rassal degisken olan X1 Xn displaystyle X 1 ldots X n birbirlerinden bagimsiz olmalari icin fX1 Xn x1 xN fX1 x1 fXn xn displaystyle f X 1 dots X n x 1 ldots x N f X 1 x 1 cdots f X n x n kosuluna tam olarak uymalari gerekir Eger n elemanli bir rassal degisken vektorunun ortak olasilik dagilimi tek bir degisken icin n degisik fonksiyona faktorize edilebilirse yani fX1 Xn x1 xn f1 x1 fn xn displaystyle f X 1 dots X n x 1 ldots x n f 1 x 1 cdots f n x n ise o halde n degiskenin hepsi birbirlerinden bagimsizlik gosteriyor demektir Bu halde her bir fonksiyon icin marjinal olasilik yogunluk fonksiyonu soyle verilir fXi xi fi yi fi x dx displaystyle f X i x i frac f i y i int f i x dx Ornegin Coklu boyutlu olasilik yogunluk fonksiyonlarinin verilen tanimini biraz daha aciga kavusturmak icin basit bir ornegin alinsin bu iki bilinmeyenli bir rassal vektor olsun Koordinatlari X Y displaystyle X Y olan iki boyutlu rassal vektor R displaystyle vec R olarak isimlendirilsin Pozitif x ve pozitif y kuadrantlari icinde R displaystyle vec R icin olasilik elde etmek soyle Pr X gt 0 Y gt 0 0 0 fX Y x y dxdy displaystyle Pr left X gt 0 Y gt 0 right int 0 infty int 0 infty f X Y x y dx dy olur Kaynakcade Laplace Pierre Simon 1812 Theorie Analytique des Probabilites fr Ilk defa olasilik kurami ile degiskenler hesabini bilestiren temel eser dd Kolmogorov Andrei Nikolajevich 1933 Grundbegriffe der Wahrscheinlichkeitrechnung de Olasilik kuraminin ilk defa modern olcu teorisi temeline konulmasi Ingilizce tercumesi Foundations of the Theory of Probability olarak 1950de yayinlanmistir dd Ayrica bakinizOlasilik dagilimi Olasilik kutle fonksiyonu Rassal degisken
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State