Küresel koordinat sistemi, nokta belirtmenin bir yoludur.

Küre üzerindeki bir nokta bu sistemde üç tane bileşenle ifade edilir, bunlar r, ve ' dir. Koordinatların tanımlı oldukları aralıklar ve tanımları şu şekilde verilir.
: Yarıçap P ve (0,0,0) noktası arasındaki uzaklıktır. Tanım aralığı olarak verilir.
: Enlem, z-ekseni ve çap arasındaki açıdır. aralığında tanımlıdır. Polar açı olarak da adlandırılır.
: Boylam, x-ekseni ile çapın xy-düzlemine () arasındaki açıdır. aralığında tanımlıdır. Diğer bir adı azimütal açıdır.
Bu sistem, dünya üzerinde coğrafi konum belirlerken kullanılan sistemdir. Dünya' nın yüzeyi üzerinde her noktada yarıçap aynı olduğundan, sadece enlem ve boylam ile bir yer belirlenebilir. Ayrıca fizikte küresel yapıya sahip sistemler, (dünya, güneş, yüklü bilye vs.) ele alınırken yine küresel koordinatlara geçiş yapılır. Küresel koordinatlarla Kartezyen koordinatlar arasındaki bağıntılar şu şekildedir.
Küresel koordinatlarda Laplasyen, diverjans ve gradyan Kartezyen koordinatlardakinden farklıdır. kullanılarak diferansiyel eleman hesaplanabileceği gibi şekilden de P noktası etrafında sonsuz küçük bir hacim elemanının büyüklüğü şu şekilde hesaplabilir.
Bu hacim elemanı bütün küre üzerinden integral alınarak R yarıçaplı kürenin hacmi bulunur.
Kalınlığı olmayan bir hacim elemanı,alan elemanı olacağından sonsuz küçük yüzey elemanı şu şekilde ele alınır.
Bu eleman bütün küre yüzeyi üzerinden integre edilirse R yarıçaplı kürenin alanı da bulunabilir.
Fizikte bu integraller herhangi bir yoğunluk fonksiyonuyla verilmiş elektrik ve yerçekimi alanındaki küreler için sıklıkla çözülür.
Küresel koordinatlarda integrasyon ve diferansiyasyon
Aşağıdaki denklemler varsayımı şu θ eğim z den (polar) axis (belirsiz x, y ve z ile karşılıklı olarak normaldir):
için 

burada
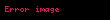






Böylece diferansiyel dir
Yüzey öge 







Böylece, örnek için, bir fonksiyon 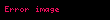
bu sistem içinde işlemcisi tanımlı değildir ve böylece gradyan, diverjans ve açıkça tanımlanmış olmalıdır:


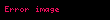

Kinematik
Bir noktanın küresel koordinatlar içinde konumu yazıldığında,
hız ise,
ve ivme,
Bir sabit φnın durumu içinde veya 
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kuresel koordinat sistemi nokta belirtmenin bir yoludur r yaricapli bir kure uzerindeki herhangi bir P noktasinin kuresel koordinatlarla gosterimi Kure uzerindeki bir nokta bu sistemde uc tane bilesenle ifade edilir bunlar r 8 displaystyle theta ve ϕ displaystyle phi dir Koordinatlarin tanimli olduklari araliklar ve tanimlari su sekilde verilir r displaystyle r Yaricap P ve 0 0 0 noktasi arasindaki uzakliktir Tanim araligi 0 r lt displaystyle 0 leq r lt infty olarak verilir 8 displaystyle theta Enlem z ekseni ve cap arasindaki acidir 0 8 180 displaystyle 0 leq theta leq 180 circ araliginda tanimlidir Polar aci olarak da adlandirilir ϕ displaystyle phi Boylam x ekseni ile capin xy duzlemine r displaystyle rho arasindaki acidir 0 ϕ lt 360 displaystyle 0 leq phi lt 360 circ araliginda tanimlidir Diger bir adi azimutal acidir Bu sistem dunya uzerinde cografi konum belirlerken kullanilan sistemdir Dunya nin yuzeyi uzerinde her noktada yaricap ayni oldugundan sadece enlem ve boylam ile bir yer belirlenebilir Ayrica fizikte kuresel yapiya sahip sistemler dunya gunes yuklu bilye vs ele alinirken yine kuresel koordinatlara gecis yapilir Kuresel koordinatlarla Kartezyen koordinatlar arasindaki bagintilar su sekildedir x rsin 8cos ϕ displaystyle x r sin theta cos phi y rsin 8sin ϕ displaystyle y r sin theta sin phi z rcos 8 displaystyle z r cos theta Kuresel koordinatlarda Laplasyen diverjans ve gradyan Kartezyen koordinatlardakinden farklidir kullanilarak diferansiyel eleman hesaplanabilecegi gibi sekilden de P noktasi etrafinda sonsuz kucuk bir hacim elemaninin buyuklugu su sekilde hesaplabilir dV rdϕ rd8 dr r2sin 8drd8dϕ displaystyle dV rho d phi rd theta dr r 2 sin theta drd theta d phi Bu hacim elemani butun kure uzerinden integral alinarak R yaricapli kurenin hacmi bulunur V dV r 0Rr2dr 8 0psin 8d8 ϕ 02pdϕ 43pR3 displaystyle V int dV int r 0 R r 2 dr int theta 0 pi sin theta d theta int phi 0 2 pi d phi frac 4 3 pi R 3 Kalinligi olmayan bir hacim elemani alan elemani olacagindan sonsuz kucuk yuzey elemani su sekilde ele alinir dA rdϕ rd8 r2sin 8d8dϕ displaystyle dA rho d phi rd theta r 2 sin theta d theta d phi Bu eleman butun kure yuzeyi uzerinden integre edilirse R yaricapli kurenin alani da bulunabilir A dA R2 8 0psin 8d8 ϕ 02pdϕ 4pR2 displaystyle A int dA R 2 int theta 0 pi sin theta d theta int phi 0 2 pi d phi 4 pi R 2 Fizikte bu integraller herhangi bir yogunluk fonksiyonuyla verilmis elektrik ve yercekimi alanindaki kureler icin siklikla cozulur Kuresel koordinatlarda integrasyon ve diferansiyasyonAsagidaki denklemler varsayimi su 8 egim z den polar axis belirsiz x y ve z ile karsilikli olarak normaldir icin r 8 f displaystyle r theta varphi dan r dr 8 d8 f df displaystyle r mathrm d r theta mathrm d theta varphi mathrm d varphi ya sonsuz yer degistirmedir dr drr rd88 rsin 8dff displaystyle mathrm d mathbf r mathrm d r boldsymbol hat r r mathrm d theta boldsymbol hat theta r sin theta mathrm d varphi mathbf boldsymbol hat varphi burada r sin 8 cos f i sin 8 sin f ȷ cos 8 k displaystyle boldsymbol hat r sin theta cos varphi boldsymbol hat imath sin theta sin varphi boldsymbol hat jmath cos theta boldsymbol hat k 8 cos 8 cos f i cos 8 sin f ȷ sin 8 k displaystyle boldsymbol hat theta cos theta cos varphi boldsymbol hat imath cos theta sin varphi boldsymbol hat jmath sin theta boldsymbol hat k f sin f i cos f ȷ displaystyle boldsymbol hat varphi sin varphi boldsymbol hat imath cos varphi boldsymbol hat jmath r 8 f displaystyle r theta varphi yukselen yon icinde yerel ortogonal birim vektorlerdir sirasiyla ve i ȷ k displaystyle boldsymbol hat imath boldsymbol hat jmath boldsymbol hat k kartezyen uzay icinde birim vektorlerdir 8 displaystyle theta dan 8 d8 displaystyle theta mathrm d theta ya germe ve r displaystyle r yaricapta sabit bir kuresel yuzey uzerinde f df displaystyle varphi mathrm d varphi ya f displaystyle varphi dir dSr r2sin 8d8df displaystyle mathrm d S r r 2 sin theta mathrm d theta mathrm d varphi Boylece diferansiyel dir dW dSrr2 sin 8d8df displaystyle mathrm d Omega frac mathrm d S r r 2 sin theta mathrm d theta mathrm d varphi Yuzey oge 8 displaystyle theta polar acinin bir yuzeyi icinde sabit baslangic kose ile bir koni tir dS8 rsin 8dfdr displaystyle mathrm d S theta r sin theta mathrm d varphi mathrm d r f displaystyle varphi guney acisinin bir yuzey icinde yuzey ogesi sabit bir dik yari duzlem dir dSf rdrd8 displaystyle mathrm d S varphi r mathrm d r mathrm d theta r dr displaystyle r mathrm d r dan r displaystyle r ya geriliyor 8 d8 displaystyle theta mathrm d theta ya 8 displaystyle theta ve f df displaystyle varphi mathrm d varphi ya f displaystyle varphi is dV r2sin 8drd8df displaystyle mathrm d V r 2 sin theta mathrm d r mathrm d theta mathrm d varphi Boylece ornek icin bir fonksiyon f r 8 f displaystyle f r theta varphi ile R3 icinde her nokta uzerinde integrallenebilir f 02p 8 0p r 0 f r 8 f r2sin 8dr d8 df displaystyle int varphi 0 2 pi int theta 0 pi int r 0 infty f r theta varphi r 2 sin theta mathrm d r mathrm d theta mathrm d varphi bu sistem icinde islemcisi tanimli degildir ve boylece gradyan diverjans ve acikca tanimlanmis olmalidir f f rr 1r f 88 1rsin 8 f ff displaystyle nabla f partial f over partial r boldsymbol hat r 1 over r partial f over partial theta boldsymbol hat theta 1 over r sin theta partial f over partial varphi boldsymbol hat varphi A 1r2 r r2Ar 1rsin 8 8 sin 8A8 1rsin 8 Af f displaystyle nabla cdot mathbf A frac 1 r 2 partial over partial r left r 2 A r right frac 1 r sin theta partial over partial theta left sin theta A theta right frac 1 r sin theta partial A varphi over partial varphi A 1rsin 8 8 Afsin 8 A8 f r 1r 1sin 8 Ar f r rAf 8 1r r rA8 Ar 8 f displaystyle nabla times mathbf A displaystyle 1 over r sin theta left partial over partial theta left A varphi sin theta right partial A theta over partial varphi right boldsymbol hat r displaystyle 1 over r left 1 over sin theta partial A r over partial varphi partial over partial r left rA varphi right right boldsymbol hat theta displaystyle 1 over r left partial over partial r left rA theta right partial A r over partial theta right boldsymbol hat varphi 2f 1r2 r r2 f r 1r2sin 8 8 sin 8 f 8 1r2sin2 8 2f f2 2 r2 2r r f 1r2sin 8 8 sin 8 8 f 1r2sin2 8 2 f2f displaystyle nabla 2 f 1 over r 2 partial over partial r left r 2 partial f over partial r right 1 over r 2 sin theta partial over partial theta left sin theta partial f over partial theta right 1 over r 2 sin 2 theta partial 2 f over partial varphi 2 left frac partial 2 partial r 2 frac 2 r frac partial partial r right f 1 over r 2 sin theta partial over partial theta left sin theta frac partial partial theta right f frac 1 r 2 sin 2 theta frac partial 2 partial varphi 2 f KinematikBir noktanin kuresel koordinatlar icinde konumu yazildiginda r rr displaystyle mathbf r r mathbf hat r hiz ise v r r r8 8 rf sin 8f displaystyle mathbf v dot r mathbf hat r r dot theta boldsymbol hat theta r dot varphi sin theta mathbf boldsymbol hat varphi ve ivme a r r8 2 rf 2sin2 8 r displaystyle mathbf a left ddot r r dot theta 2 r dot varphi 2 sin 2 theta right mathbf hat r r8 2r 8 rf 2sin 8cos 8 8 displaystyle left r ddot theta 2 dot r dot theta r dot varphi 2 sin theta cos theta right boldsymbol hat theta rf sin 8 2r f sin 8 2r8 f cos 8 f displaystyle left r ddot varphi sin theta 2 dot r dot varphi sin theta 2r dot theta dot varphi cos theta right mathbf boldsymbol hat varphi Bir sabit fnin durumu icinde veya 8 p2 displaystyle theta tfrac pi 2 bu indirgenir Ayrica bakinizGPS Cografi koordinat sistemi Silindirik ve kuresel koordinatlarda del Kure Kuresel harmonikler Silindirik ve kuresel koordinatlarda vektor alani
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State