Günlük kullanımıyla küre kusursuz simetriye sahip geometrik bir nesnedir, bir yüzeydir; üç boyutlu Öklit uzayında (R3) .

Analitik geometride (x0, y0, z0) merkezli ve r yarıçaplı küre denklemi:
olarak verilir. Bu ifade, başnoktaya (orijin) uzaklıkları r olan noktaları anlatır.
Yine günlük kullanımda, içi dolu bir küreye de küre denmektedir. Matematikte ikisi arasında ayrım gözetilir ve içi dolu bir küreye denir. Bir yuvar (geometrik) bir nesne olarak 3 boyutludur. İçi boş olan küreyse 2 boyutludur.
Genel olarak, matematikte küre, n boyutlu bir çokkatlıdır. Sn olarak gösterilir. (n+1) boyutlu Öklit uzayında (Rn+1) yatar. (a0, a1,, an) merkezli ve r yarıçaplı küre Rn+1'de analitik olarak:
ile tanımlanır. Dolayısıyla, 1 boyutlu küre bir çemberdir. 0 boyutlu küreyse iki noktadan oluşur çünkü gerçel çizgide 0'a uzaklığı r olan iki nokta vardır. Rn+1'de başnokta merkezli ve 1 yarıçaplı bir küreye birim küre denir.
Formüller
(İki boyutlu, standart) bir küre için bazı formüller:
| Küre formülleri | ||
|---|---|---|
| Hacim |  | |
| Projeksiyon Alanı |  | |
| Küre parçasının hacmi |  | |
| Yarıçap | 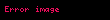 | |
| Çap | d | |
| Yükseklik | 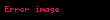 | |
| Atalet momenti |  | |
| Yüzey alanı |  | |
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Gunluk kullanimiyla kure kusursuz simetriye sahip geometrik bir nesnedir bir yuzeydir uc boyutlu Oklit uzayinda R3 Analitik geometride x0 y0 z0 merkezli ve r yaricapli kure denklemi x x0 2 y y0 2 z z0 2 r2 displaystyle x x 0 2 y y 0 2 z z 0 2 r 2 olarak verilir Bu ifade basnoktaya orijin uzakliklari r olan noktalari anlatir Yine gunluk kullanimda ici dolu bir kureye de kure denmektedir Matematikte ikisi arasinda ayrim gozetilir ve ici dolu bir kureye denir Bir yuvar geometrik bir nesne olarak 3 boyutludur Ici bos olan kureyse 2 boyutludur Genel olarak matematikte kure n boyutlu bir cokkatlidir Sn olarak gosterilir n 1 boyutlu Oklit uzayinda Rn 1 yatar a0 a1 displaystyle ldots an merkezli ve r yaricapli kure Rn 1 de analitik olarak x0 a0 2 x1 a1 2 xn an 2 r2 displaystyle x 0 a 0 2 x 1 a 1 2 ldots x n a n 2 r 2 ile tanimlanir Dolayisiyla 1 boyutlu kure bir cemberdir 0 boyutlu kureyse iki noktadan olusur cunku gercel cizgide 0 a uzakligi r olan iki nokta vardir Rn 1 de basnokta merkezli ve 1 yaricapli bir kureye birim kure denir Formuller Iki boyutlu standart bir kure icin bazi formuller Kure formulleriHacim V 43pr3 displaystyle V frac 4 3 pi r 3 Projeksiyon Alani APF pr2 displaystyle A PF pi r 2 Kure parcasinin hacmi VKS h2p3 3r h displaystyle V KS frac h 2 pi 3 3r h Yaricap r displaystyle r Cap dYukseklik h displaystyle h Atalet momenti J 25mr2 displaystyle J frac 2 5 mr 2 Yuzey alani A 4pr2 d2p displaystyle A 4 pi r 2 d 2 pi Ayrica bakinizMatematiksel sekillerin listesi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State


