Hiperişlem, matematik'te aritmetik işlemlerin sonsuz dizisidir. , ardından toplama, çarpma ve üs almanın devam eden ve ardından ikili işlemlerin ötesine geçerek serilerle ilerleyen bir işlemdir. Üstelden sonraki işlemler için bu dizinin n. elemanı tarafından adlandırıldı. n sonra -syon son eki kullanılarak (tetrasyon, gibi) elde edilir ve Knuth yukarı ok gösterimindeki n-2 okları kullanılarak yazılabilir. Her hiperişlem, önceki terimlerin (yinelemesi) olarak tanımlanır. Ackermann işlevi, Knuth yukarı ok gösterimini kullanarak şöyle yinelenebilir:
Bu yinelemeli kural, hiperişlemde yaygın olarak kullanılır (aşağıya bakınız).
Tanım
Hiperişlem dizisi, 

(n = 0 için, ikili işlemin ilk argümanı göz ardı edilerek elde edilir.)
n = 0, 1, 2, 3 için bu tanım, (ardıl) (birli işlem), toplama, çarpma ve üs almanın temel artimetik işlemlerini sırasıyla şu şekilde yeniden üretir;
ve n ≥ 4 için, bu temel işlemleri, üs almanın da ötesine götürerek Knuth yukarı ok gösterimiyle şöyle yazabiliriz;
- ...
- ...
Knuth gösterimi ≥ -2 negatif altgöstergelerinde (indislerinde), tüm hiperişlem dizisi için geçerli olduğunu kabul ederek, genişletilebilir, Sadece aşağıdaki altgösterge aralığı hariç:
"Sonraki dizi nedir?" sorusunun cevabını hiperişlem şunlarla gösterebilir: Ardıl, toplama, çarpma, üs alma ve böylece devam eder.
Temel aritmetik işlemler arasındaki ilişki, yukarıda da gösterildiği gibi, daha yüksek işlem tanımlanarak gösterilir. Hiperişlem hiyerarşisinin parametreleri, bazen kendi örnek hiperişlem terimi; tarafından ifade edilir. Böylece a taban, b üs (veya hiperüs) ve n de derece (veya kademe)dir.
Genellikle hiperişlemler, önceki hiperişlem tekrarının yükseliş tabanında, artan birleşim sayılarının yolları olarak bilinir. Ardıl, toplama, çarpma ve üs alma kavramlarının hepsi hiperişlemdir. Ardıl işlemi (x den x+1 üretme) en ilkelidir. 1'lerin sayısını belirten toplama işareti, son değeri üretene kadar kendine eklenir. Çarpma, kendisiyle kaç kez tekrarlandığını ifade eder. Üs alma, kendisiyle kaç kez çarpıldığının sayısını ifade eder.
Örnekler
Aşağıda, ilk yedi hiperişlemin listesi görülüyor.
| n | İşlem | Tanım | Adlar | Bölge |
|---|---|---|---|---|
| 0 |  |  | hiper0, artış, ardıl, zerasyon | b rastgele |
| 1 |  |  | hiper1, toplama | rastgele |
| 2 | 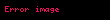 |  | hiper2, çarpma | rastgele |
| 3 |  |  | hiper3, üstel | a > 0, b reel veya a sıfır olmayan, b tam sayı |
| 4 | 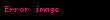 |  | hiper4, tetrasyon | a > 0, b (tam sayı) ≥ −1 |
| 5 | 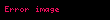 veya veya  |  | hiper5, | a ve b tam sayı, a > 0, b ≥ 0 |
| 6 |  |  | hyper6, hekzasyon | a ve b tam sayı, a > 0, b ≥ 0 |
Knuth gösterimindeki (değerlerin tablolarına) bakınız.
Tarihçe
Hiperişlemlerle ilgili ilk tartışma 1914'te Albert Bennett'in, değişmeli hiperişlemleri geliştirdiğinde başladı. Yaklaşık 12 yıl sonra hiperişlem dizisine benzeyen 
1947'de , hiperişlem olarak adlandırılan özel işlemler dizisini geliştirdi ve genişleyen üslü işlemleri ifade edebilmek için Yunanca adlar olan tetrasyon, pentasyon, hekzasyon, vb. önerdi. Örn 

Gösterimler
Aşağıdaki, hiperişlemlerde kullanılan gösterimlerin bir listesidir.
| Ad | Gösterimin  deki eşdeğeri deki eşdeğeri | Açıklama |
|---|---|---|
| Knuth yukarı ok gösterimi |  | (n ≥ 2 için) Knuth tarafından kullanıldı ve birkaç referans kitap bulundu. |
| Goodstein gösterimi |  | tarafından kullanıldı. |
| Özgün Ackermann işlevi |  | tarafından kullanıldı. |
| Ackermann–Péter fonksiyonu |  | Bu gösterim, hiperişlemlerdeki 2'ye karşılır gelir. |
| Nambiar gösterimi |  | Nambiar tarafından kullanıldı. |
| Kutu gösterimi |  | Romerio tarafından kullanıldı |
| Üstgösterge yazımı |  | Robert Munafo tarafından kullanıldı |
| Altgösterge yazımı |  | Düşük hiperişlemleri ifade etmesi için Robert Munafo tarafından kullanıldı |
| Köşeli parantez gösterimi |  | Birçok online forumda kullanıldı. ASCII için uygundur. |
Genelleştirme
Farklı başlangıç şartları veya farklı özyineleme kuralları için birçok işlem ortaya çıktı. Bazı matematikçiler tümünü, hiperişlemlerin örnekleri olarak kabul ediyor.
Genel duyarlılık, bir 




(toplama),
(çarpma) ve
(üs almadır).
Hiperişlemde çözüm aranılan açık bir problem, hiperişlem hiyerarşisi 


![image]() 'dan başlamanın farkı
'dan başlamanın farkı
1928'de , 3 argümanlı 

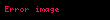




| n | İşlem | Açıklama |
|---|---|---|
| 0 |  | |
| 1 |  | |
| 2 |  | |
| 3 |  | Tetrasyonun bir formu. Bu işlemin tekrarı, tetrasyonun çok farklıdır. |
| 4 |  | karıştırmayın. |
Kullanılan diğer başlangıç şartı, 

0'dan başlamanın farkı
1984'te, C. W. Clenshaw ve F. W. J. Olver, bilgisayardaki kayan noktaların akışını engellemek için hiperişlemlerin kullanımıyla ilgili tartışma başlattı
| n | İşlem | Açıklama |
|---|---|---|
| 1 |  | |
| 2 |  | |
| 3 |  | |
| 4 |  | Tetrasyonun bir formu. Bu işlemin tekrarı tetrasyonun çok farklıdır. |
| 5 |  | karıştırmayın. |
Değişimli hiperişlemler
Değişimli hiperişlemler 1914 başlarında Albert Bennett tarafından dikkate alındı. Değişimli hiperişlemler özyineleme kuralı tarafından tanımlanır
bu, a ve b de simetriktir ve tüm hiperişlemlerin değişimli olduğu anlamına gelir. Bu dizi üstelleri içermez ve bu yüzden hiperişlem hiyerarşisi formu değildir.
| n | İşlem | Açıklama |
|---|---|---|
| 0 |  | |
| 1 |  | |
| 2 |  | Logaritmanın özelliklerinden dolayı. |
| 3 |  | Üstelin birleşme formu. |
| 4 |  | Tetrasyonla karıştırmayın. |
Dengeli hiperişlemler
Dengeli hiperişlemler, ilk önce Clément Frappier tarafından 1991'de ortaya atıldı. 
Bu, süreklilik iterasyonunu, hatta b tam sayıları için bile gereklidir.
| n | İşlem | Açıklama |
|---|---|---|
| 0 | 0. derece yoktur. | |
| 1 |  | |
| 2 |  | |
| 3 |  | Bu üstür. |
| 4 |  | Tetrasyonla karıştırmayın. |
Düşük hiperişlemler
Bu hiperişlemlere bir alternatif, soldan sağa doğru işlem yaparak şöyle elde edilir.
bu (° veya altgösterge ile) tanımlanır 



Fakat bu, geleneksel "üslü kule" formundaki kusurdan dolayı biraz düştü, Fakat şu hiper4 hariç: 
n>3 için 

| n | İşlem | Açıklama |
|---|---|---|
| 0 |  | artış, ardıl, zarasyon |
| 1 |  | |
| 2 |  | |
| 3 |  | Bu üstür. |
| 4 |  | Tetrasyonla karıştırmayın. |
| 5 |  | karıştırmayın. |
Ayrıca bakınız
Notlar
- ^ Eğer 0.derece dengeli hiperişlem olsaydı
ardından toplama
olurdu. Bu eşitlikte
koyarak
elde edilir ki, bu da çelişkidir .
Alıntı
- ^ G. F. Romerio (21 Ocak 2008). . Tetrasyon Forumu. 2 Ekim 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Nisan 2009.
|yayımcı=dış bağlantı ()
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Hiperislem matematik te aritmetik islemlerin sonsuz dizisidir ardindan toplama carpma ve us almanin devam eden ve ardindan ikili islemlerin otesine gecerek serilerle ilerleyen bir islemdir Ustelden sonraki islemler icin bu dizinin n elemani tarafindan adlandirildi n sonra syon son eki kullanilarak tetrasyon gibi elde edilir ve Knuth yukari ok gosterimindeki n 2 oklari kullanilarak yazilabilir Her hiperislem onceki terimlerin yinelemesi olarak tanimlanir Ackermann islevi Knuth yukari ok gosterimini kullanarak soyle yinelenebilir a nb a n 1 a n b 1 displaystyle a uparrow n b a uparrow n 1 left a uparrow n b 1 right Bu yinelemeli kural hiperislemde yaygin olarak kullanilir asagiya bakiniz TanimHiperislem dizisi n N displaystyle n in mathbb N olmak uzere Hn N N N displaystyle H n mathbb N times mathbb N rightarrow mathbb N ikili islemlerinin dizisidir ve yinelemesi soyle tanimlanir Hn a b b 1n 0ise an 1 b 0ise 0n 2 b 0ise 1n 3 b 0ise Hn 1 a Hn a b 1 aksi takdirde displaystyle H n a b begin cases b 1 amp n 0 text ise a amp n 1 b 0 text ise 0 amp n 2 b 0 text ise 1 amp n geq 3 b 0 text ise H n 1 a H n a b 1 amp text aksi takdirde end cases n 0 icin ikili islemin ilk argumani goz ardi edilerek elde edilir n 0 1 2 3 icin bu tanim ardil birli islem toplama carpma ve us almanin temel artimetik islemlerini sirasiyla su sekilde yeniden uretir H0 a b b 1 displaystyle H 0 a b b 1 H1 a b a b displaystyle H 1 a b a b H2 a b a b displaystyle H 2 a b a cdot b H3 a b ab displaystyle H 3 a b a b ve n 4 icin bu temel islemleri us almanin da otesine goturerek Knuth yukari ok gosterimiyle soyle yazabiliriz H4 a b a b displaystyle H 4 a b a uparrow uparrow b H5 a b a b displaystyle H 5 a b a uparrow uparrow uparrow b Hn a b a n 2b n 3 icin displaystyle H n a b a uparrow n 2 b n geq 3 mbox icin Knuth gosterimi 2 negatif altgostergelerinde indislerinde tum hiperislem dizisi icin gecerli oldugunu kabul ederek genisletilebilir Sadece asagidaki altgosterge araligi haric Hn a b a n 2b n 0 icin displaystyle H n a b a uparrow n 2 b n geq 0 mbox icin Sonraki dizi nedir sorusunun cevabini hiperislem sunlarla gosterebilir Ardil toplama carpma us alma ve boylece devam eder a b 1 a b 1 displaystyle a b 1 a b 1 a b a a b 1 displaystyle a cdot b a a cdot b 1 ab a a b 1 displaystyle a b a cdot a b 1 Temel aritmetik islemler arasindaki iliski yukarida da gosterildigi gibi daha yuksek islem tanimlanarak gosterilir Hiperislem hiyerarsisinin parametreleri bazen kendi ornek hiperislem terimi tarafindan ifade edilir Boylece a taban b us veya hiperus ve n de derece veya kademe dir Genellikle hiperislemler onceki hiperislem tekrarinin yukselis tabaninda artan birlesim sayilarinin yollari olarak bilinir Ardil toplama carpma ve us alma kavramlarinin hepsi hiperislemdir Ardil islemi x den x 1 uretme en ilkelidir 1 lerin sayisini belirten toplama isareti son degeri uretene kadar kendine eklenir Carpma kendisiyle kac kez tekrarlandigini ifade eder Us alma kendisiyle kac kez carpildiginin sayisini ifade eder OrneklerAsagida ilk yedi hiperislemin listesi goruluyor n Islem Tanim Adlar Bolge0 b 1 displaystyle b 1 1 1 1 1 1 b displaystyle 1 underbrace 1 1 1 cdots 1 b hiper0 artis ardil zerasyon b rastgele1 a b displaystyle a b a 1 1 1 1 b displaystyle a underbrace 1 1 1 cdots 1 b hiper1 toplama rastgele2 a b displaystyle a cdot b a a a a b displaystyle underbrace a a a cdots a atop b hiper2 carpma rastgele3 a b ab displaystyle a uparrow b a b a a a a a b displaystyle underbrace a cdot a cdot a cdot a cdot ldots cdot a atop b hiper3 ustel a gt 0 b reel veya a sifir olmayan b tam sayi4 a b displaystyle a uparrow uparrow b a a a a b displaystyle underbrace a uparrow a uparrow a uparrow cdots uparrow a atop b hiper4 tetrasyon a gt 0 b tam sayi 15 a b displaystyle a uparrow uparrow uparrow b veya a 3b displaystyle a uparrow 3 b a a a b displaystyle underbrace a uparrow uparrow a uparrow uparrow cdots uparrow uparrow a atop b hiper5 a ve b tam sayi a gt 0 b 06 a 4b displaystyle a uparrow 4 b a 3a 3 3a b displaystyle underbrace a uparrow 3 a uparrow 3 cdots uparrow 3 a atop b hyper6 hekzasyon a ve b tam sayi a gt 0 b 0 Knuth gosterimindeki degerlerin tablolarina bakiniz TarihceHiperislemlerle ilgili ilk tartisma 1914 te Albert Bennett in degismeli hiperislemleri gelistirdiginde basladi Yaklasik 12 yil sonra hiperislem dizisine benzeyen ϕ a b n displaystyle phi a b n fonksiyonunu tanimladi 1947 de hiperislem olarak adlandirilan ozel islemler dizisini gelistirdi ve genisleyen uslu islemleri ifade edebilmek icin Yunanca adlar olan tetrasyon pentasyon hekzasyon vb onerdi Orn G n a b Hn a b displaystyle G n a b H n a b gibi uc argumanli degiskenli fonksiyonun hiperislem dizisi ozgun ϕ a b n displaystyle phi a b n Ackermann islevinin bir cesididir GosterimlerAsagidaki hiperislemlerde kullanilan gosterimlerin bir listesidir Ad Gosterimin Hn a b displaystyle H n a b deki esdegeri AciklamaKnuth yukari ok gosterimi a n 2b displaystyle a uparrow n 2 b n 2 icin Knuth tarafindan kullanildi ve birkac referans kitap bulundu Goodstein gosterimi G n a b displaystyle G n a b tarafindan kullanildi Ozgun Ackermann islevi ϕ a b n 1 1 n 3 icin ϕ a b 1 n 1 n gt 3 icin displaystyle begin matrix phi a b n 1 1 leq n leq 3 mbox icin phi a b 1 n 1 n gt 3 mbox icin end matrix tarafindan kullanildi Ackermann Peter fonksiyonu A n b 3 3 a 2 icin displaystyle A n b 3 3 a 2 text icin Bu gosterim hiperislemlerdeki 2 ye karsilir gelir Nambiar gosterimi a nb displaystyle a otimes n b Nambiar tarafindan kullanildi Kutu gosterimi anb displaystyle a begin array c hline n hline end array b Romerio tarafindan kullanildiUstgosterge yazimi a n b displaystyle a n b Robert Munafo tarafindan kullanildiAltgosterge yazimi a n b displaystyle a n b Dusuk hiperislemleri ifade etmesi icin Robert Munafo tarafindan kullanildiKoseli parantez gosterimi a n b displaystyle a n b Bircok online forumda kullanildi ASCII icin uygundur GenellestirmeFarkli baslangic sartlari veya farkli ozyineleme kurallari icin bircok islem ortaya cikti Bazi matematikciler tumunu hiperislemlerin ornekleri olarak kabul ediyor Genel duyarlilik bir S I F displaystyle S I F hiperislem hiyerarsisi ikili islemin S displaystyle S deki Fn n I displaystyle F n n in I dir ve i j k I displaystyle i j k in I sartini saglayan I displaystyle I tarafindan dizinlenir Burada Fi a b a b displaystyle F i a b a b toplama Fj a b a b displaystyle F j a b a cdot b carpma ve Fk a b ab displaystyle F k a b a b us almadir Hiperislemde cozum aranilan acik bir problem hiperislem hiyerarsisi N N F displaystyle mathbb N mathbb N F nin C C F displaystyle mathbb C mathbb C F yi genellestirebilecegimi yoksa C Fn displaystyle mathbb C F n nin gibi davranacagi kisitli tricted domains a displaystyle a dan baslamanin farki 1928 de 3 argumanli ϕ a b n displaystyle phi a b n fonksiyonunu tanimladi Bu 2 argumanli olan ve Ackermann islevi olarak bilinen fonksiyonun azar azar gelistirilmis seklidir Ozgun Ackermann islevi olan ϕ displaystyle phi modern hiperislemlere birazcik benziyordu Cunku onun baslangic sartlari tum n gt 2 displaystyle n gt 2 icin ϕ a 0 n a displaystyle phi a 0 n a dan baslar Ayrica eklemeyi n 0 displaystyle n 0 a carpmayi n 1 displaystyle n 1 e ve us almayi n 2 displaystyle n 2 a atadi Boylece baslangic sartlari tetrasyon ve ilerisi icin cok farkli islemler uretti n Islem Aciklama0 F0 a b a b displaystyle F 0 a b a b 1 F1 a b a b displaystyle F 1 a b a cdot b 2 F2 a b ab displaystyle F 2 a b a b 3 F3 a b a b 1 displaystyle F 3 a b a uparrow uparrow b 1 Tetrasyonun bir formu Bu islemin tekrari tetrasyonun cok farklidir 4 F4 a b x a x 1 b a displaystyle F 4 a b x to a uparrow uparrow x 1 b a karistirmayin Kullanilan diger baslangic sarti A 0 b 2b 1 displaystyle A 0 b 2b 1 buradaki taban sabit olan a 2 displaystyle a 2 dir 0 dan baslamanin farki 1984 te C W Clenshaw ve F W J Olver bilgisayardaki kayan noktalarin akisini engellemek icin hiperislemlerin kullanimiyla ilgili tartisma baslatti n Islem Aciklama1 F1 a b a b displaystyle F 1 a b a b 2 F2 a b a b eln a ln b displaystyle F 2 a b a cdot b e ln a ln b 3 F3 a b ab displaystyle F 3 a b a b 4 F4 a b a b 1 displaystyle F 4 a b a uparrow uparrow b 1 Tetrasyonun bir formu Bu islemin tekrari tetrasyonun cok farklidir 5 F5 a b x a x 1 b 0 displaystyle F 5 a b x to a uparrow uparrow x 1 b 0 karistirmayin Degisimli hiperislemler Degisimli hiperislemler 1914 baslarinda Albert Bennett tarafindan dikkate alindi Degisimli hiperislemler ozyineleme kurali tarafindan tanimlanir Fn 1 a b exp Fn ln a ln b displaystyle F n 1 a b exp F n ln a ln b bu a ve b de simetriktir ve tum hiperislemlerin degisimli oldugu anlamina gelir Bu dizi ustelleri icermez ve bu yuzden hiperislem hiyerarsisi formu degildir n Islem Aciklama0 F0 a b ln ea eb displaystyle F 0 a b ln e a e b 1 F1 a b a b displaystyle F 1 a b a b 2 F2 a b a b eln a ln b displaystyle F 2 a b a cdot b e ln a ln b Logaritmanin ozelliklerinden dolayi 3 F3 a b eln a ln b displaystyle F 3 a b e ln a ln b Ustelin birlesme formu 4 F4 a b eeln ln a ln ln b displaystyle F 4 a b e e ln ln a ln ln b Tetrasyonla karistirmayin Dengeli hiperislemler Dengeli hiperislemler ilk once Clement Frappier tarafindan 1991 de ortaya atildi xx displaystyle x x fonksiyon tekrarinin temelini olusturur ve bu yuzden Steinhaus Moser gosterimi ile iliskilidir Dengeli hiperislemlerde kullanilan ozyineleme kurali sudur Fn 1 a b x Fn x x log2 b a displaystyle F n 1 a b x to F n x x log 2 b a Bu sureklilik iterasyonunu hatta b tam sayilari icin bile gereklidir n Islem Aciklama0 0 derece yoktur 1 F1 a b a b displaystyle F 1 a b a b 2 F2 a b a b a2log2 b displaystyle F 2 a b a cdot b a2 log 2 b 3 F3 a b ab a2log2 b displaystyle F 3 a b a b a 2 log 2 b Bu ustur 4 F4 a b x xx log2 b a displaystyle F 4 a b x to x x log 2 b a Tetrasyonla karistirmayin Dusuk hiperislemler Bu hiperislemlere bir alternatif soldan saga dogru islem yaparak soyle elde edilir a b a b 1 1 displaystyle a b a b 1 1 a b a b 1 a displaystyle a cdot b a cdot b 1 a ab a b 1 a displaystyle a b a b 1 cdot a bu veya altgosterge ile tanimlanir a n 1 b a n 1 b 1 n a displaystyle a n 1 b a n 1 b 1 n a ile a 1 b a b displaystyle a 1 b a b a 2 0 0 displaystyle a 2 0 0 ve n gt 2 displaystyle n gt 2 icin a n 0 1 displaystyle a n 0 1 dir Fakat bu geleneksel uslu kule formundaki kusurdan dolayi biraz dustu Fakat su hiper4 haric a 4 b a a b 1 displaystyle a 4 b a a b 1 n gt 3 icin a n b displaystyle a n b nasil a n b displaystyle a n b den cok farkli olabilir ki Bu simetriden dolayi ve icinde tanimlanan birlesme olarak adlandirilir cisime bakiniz fakat eksik n Islem Aciklama0 b 1 displaystyle b 1 artis ardil zarasyon1 F1 a b a b displaystyle F 1 a b a b 2 F2 a b a b displaystyle F 2 a b a cdot b 3 F3 a b ab displaystyle F 3 a b a b Bu ustur 4 F4 a b aa b 1 displaystyle F 4 a b a a b 1 Tetrasyonla karistirmayin 5 F5 a b x xx a 1 b 1 a displaystyle F 5 a b x to x x a 1 b 1 a karistirmayin Ayrica bakinizBuyuk sayilarNotlar Eger 0 derece dengeli hiperislem olsaydi f a b displaystyle f a b ardindan toplama a b x f x x log2 b a displaystyle a b x to f x x log 2 b a olurdu Bu esitlikte b 1 displaystyle b 1 koyarak a 1 x f x x 0 a a displaystyle a 1 x to f x x 0 a a elde edilir ki bu da celiskidir Alinti G F Romerio 21 Ocak 2008 Tetrasyon Forumu 2 Ekim 2011 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Nisan 2009 yayimci dis baglanti yardim
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

























