Hata marjı ya da hata payı bir anketin sonuçlarındaki rastgele örnekleme hatası miktarını ifade eden bir istatistiktir. Hata payı ne kadar büyükse, anket sonucunun yığın özelliklerini yansıtacağına duyulan güven o kadar az olmalıdır. Bir popülasyon eksik örneklenip çıktı ölçüsü pozitif varyansa sahip olduğunda, yani ölçü değiştiğinde, hata marjı pozitif olur.

Hata marjı terimi genellikle anket dışı bağlamlarda ölçülen miktarların raporlanmasında oluşan belirtmek için kullanılır. Aynı zamanda konuşma dilinde, bir hedefe ulaşmada sahip olabileceğiniz alan veya esneklik miktarına atıfta bulunmak için de kullanılmaktadır. Örneğin, sporda genellikle tarafından bir hedef, puan veya sonuca ulaşmak için ne kadar hassasiyetin gerekli olduğunu açıklarken kullanılır. Bowlingte kullanılan pinler 4,75 inç genişliğinde, top ise 8,5 inç genişliğindedir, bu nedenle bir bowling sporcusunun ikinci atışta kalan belirli bir pini düşürmek için 21,75 inç hata payı olduğu söylenebilir (örnek olarak 1 veya 5 numaralı pinler gösterilebilir, 7 ve 10 numaralı pinler hat kenarında olduklarından aynı hata marjına sahip değildir).
Konsept
Basit bir evet / hayır anketini ele alalım 











göre 

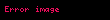
Genellikle 



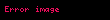
hata payına sahiptir.
Standart sapma ve standart hata
Normal dağılan 



Anket sonuçlarından biri için şu varsayılır: 



Farklı güven seviyelerinde maksimum hata payı











 |  |  |  | |
|---|---|---|---|---|
| 0.68 | 0,994457883210 | 0.999 | 3,290526731492 | |
| 0.90 | 1,644853626951 | 0.9999 | 3,890591886413 | |
| 0.95 | 1,959963984540 | 0.99999 | 4,417173413469 | |
| 0.98 | 2,326347874041 | 0.999999 | 4,891638475699 | |
| 0,99 | 2,575829303549 | 0,9999999 | 5,326723886384 | |
| 0.995 | 2,807033768344 | 0,99999999 | 5,730728868236 | |
| 0,997 | 2,967737925342 | 0,999999999 | 6,109410204869 |










Ayrıca, bildirilen herhangi bir 
Kaynakça
Dış bağlantılar
- "Errors, theory of", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Margin of Error". MathWorld.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Hata marji ya da hata payi bir anketin sonuclarindaki rastgele ornekleme hatasi miktarini ifade eden bir istatistiktir Hata payi ne kadar buyukse anket sonucunun yigin ozelliklerini yansitacagina duyulan guven o kadar az olmalidir Bir populasyon eksik orneklenip cikti olcusu pozitif varyansa sahip oldugunda yani olcu degistiginde hata marji pozitif olur Her biri 95 guven araligina asagida hata payina solda ve ornek boyutuna sagda sahip farkli boyutlardaki anketlerin renklerle kodlanmis olasilik yogunluklari Her aralik 2 ceyreklik verildiginde 95 guvenle gercek degerlerin bulunabilecegi araligi yansitir Hata payi guven araliginin yarisidir ayrica araligin yaricapi Ornek ne kadar buyukse hata payi o kadar kucuk olur Ayrica ornek raporlanan 2 ceyreklikten ne kadar uzaksa hata payi da o kadar kucuk olur Hata marji terimi genellikle anket disi baglamlarda olculen miktarlarin raporlanmasinda olusan belirtmek icin kullanilir Ayni zamanda konusma dilinde bir hedefe ulasmada sahip olabileceginiz alan veya esneklik miktarina atifta bulunmak icin de kullanilmaktadir Ornegin sporda genellikle tarafindan bir hedef puan veya sonuca ulasmak icin ne kadar hassasiyetin gerekli oldugunu aciklarken kullanilir Bowlingte kullanilan pinler 4 75 inc genisliginde top ise 8 5 inc genisligindedir bu nedenle bir bowling sporcusunun ikinci atista kalan belirli bir pini dusurmek icin 21 75 inc hata payi oldugu soylenebilir ornek olarak 1 veya 5 numarali pinler gosterilebilir 7 ve 10 numarali pinler hat kenarinda olduklarindan ayni hata marjina sahip degildir KonseptBasit bir evet hayir anketini ele alalim P displaystyle P N displaystyle N ile ifade edilen bir populasyondan cekilen n displaystyle n adet katilimcinin cevaplarinin ornegi n lt lt N displaystyle n lt lt N ve p displaystyle p verdikleri evet cevaplarinin yuzdesi olsun p displaystyle p sonucunun tum N displaystyle N populasyonuna uygulanacak bir anketin gercek sonucuna bu anketi gercekten uygulamak zorunda kalmadan ne kadar yakin ciktigini bilmek isteriz Varsayimsal olarak N displaystyle N populasyonundan yeni cekilen sonraki n displaystyle n adet katilimcinin cevaplarinin p1 p2 displaystyle p 1 p 2 ldots p displaystyle overline p uzerinde normal dagilmasini bekleriz Hata payi bu sonuclarin belirli bir yuzdesinin p displaystyle overline p den farkina iliskin beklenilen mesafeyi tanimlar gore p1 p2 displaystyle p 1 p 2 ldots sonuclarinin 95 inin gercek ortalamanin p displaystyle overline p her iki tarafinda yaklasik iki standart sapma 2sP displaystyle pm 2 sigma P araligina dusmesini bekleriz Bu araliga guven araligi adi verilir ve yaricap araligin yarisi 95 guven duzeyine karsilik gelen hata payi olarak adlandirilir Genellikle g displaystyle gamma guven duzeyinde n displaystyle n ornek boyutuna sahip bir populasyonun beklenen standart sapmasi s displaystyle sigma zg displaystyle z gamma ceyreklik acikligini ayrica bir z skorunu ve s2n displaystyle sqrt frac sigma 2 n standart hatayi gosterirken MOEg zg s2n displaystyle MOE gamma z gamma times sqrt frac sigma 2 n hata payina sahiptir Standart sapma ve standart hataNormal dagilan p1 p2 displaystyle p 1 p 2 ldots degerlerinin n displaystyle n ile degisen bir standart sapmaya sahip olmasini bekleriz Daha kucuk n displaystyle n daha genis hata payi anlamina gelir Buna standart hata denir sp displaystyle sigma overline p Anket sonuclarindan biri icin su varsayilir p p displaystyle p overline p ve sonraki tum sonuclar p1 p2 displaystyle p 1 p 2 ldots birlikte bir varyansa sahiptir sP2 P 1 P displaystyle sigma P 2 P 1 P Standart hata sp sP2n p 1 p n displaystyle text Standart hata sigma overline p approx sqrt frac sigma P 2 n approx sqrt frac p 1 p n p 1 p displaystyle p 1 p bir Bernoulli dagiliminin varyansina karsilik gelir Farkli guven seviyelerinde maksimum hata payig displaystyle gamma guven duzeyi icin ortalama ile ilgili bir guven araligi m zgs displaystyle mu pm z gamma sigma yani m zgs m zgs displaystyle mu z gamma sigma mu z gamma sigma seklindedir P displaystyle P degerleri g displaystyle gamma olasilikla bu aralik icine dusmelidir zg displaystyle z gamma nin kesin degerleri normal dagilimin ceyrekler acikligi fonksiyonu ile verilir ve 68 95 99 7 kuralina yakinsar zg displaystyle z gamma g 1 displaystyle gamma geq 1 icin tanimsizdir yani z1 00 displaystyle z 1 00 gibi z1 10 displaystyle z 1 10 de tanimsizdir g displaystyle gamma zg displaystyle z gamma g displaystyle gamma zg displaystyle z gamma 0 68 0 994457883210 0 999 3 2905267314920 90 1 644853626951 0 9999 3 8905918864130 95 1 959963984540 0 99999 4 4171734134690 98 2 326347874041 0 999999 4 8916384756990 99 2 575829303549 0 9999999 5 3267238863840 995 2 807033768344 0 99999999 5 7307288682360 997 2 967737925342 0 999999999 6 109410204869 p 0 5 displaystyle p 0 5 iken maxsP2 maxP 1 P 0 25 displaystyle max sigma P 2 max P 1 P 0 25 oldugundan p p 0 5 displaystyle p overline p 0 5 seklinde keyfi bir ayarlama ile g displaystyle gamma guven seviyesinde ve n displaystyle n ornek boyutunda gercek sonuclari almadan once bile P displaystyle P nin maksimum hata payini elde etmek icin sP displaystyle sigma P sp displaystyle sigma overline p ve zgsp displaystyle z gamma sigma overline p degerleri hesaplanabilir Ornegin p 0 5 n 1013 displaystyle p 0 5 n 1013 iken MOE95 0 5 z0 95sp z0 95sP2n 1 96 25n 0 98 n 3 1 displaystyle MOE 95 0 5 z 0 95 sigma overline p approx z 0 95 sqrt frac sigma P 2 n 1 96 sqrt frac 25 n 0 98 sqrt n pm 3 1 MOE99 0 5 z0 99sp z0 99sP2n 2 58 25n 1 29 n 4 1 displaystyle MOE 99 0 5 z 0 99 sigma overline p approx z 0 99 sqrt frac sigma P 2 n 2 58 sqrt frac 25 n 1 29 sqrt n pm 4 1 Ayrica bildirilen herhangi bir MOE95 displaystyle MOE 95 icin MOE99 z0 99z0 95MOE95 1 3 MOE95 displaystyle MOE 99 frac z 0 99 z 0 95 MOE 95 approx 1 3 times MOE 95 KaynakcaSudman Seymour ve Bradburn Norman 1982 Sorular Sormak Anket Tasarimi Icin Pratik Bir Kilavuz San Francisco Jossey Bass 0 87589 546 8ISBN 0 87589 546 8 Introductory Statistics 5th Wiley 1990 ISBN 0 471 61518 8 Introductory Statistics 5th Wiley 1990 ISBN 0 471 61518 8 Introductory Statistics 5th Wiley 1990 ISBN 0 471 61518 8 Dis baglantilar Errors theory of Encyclopedia of Mathematics EMS Press 2001 1994 Weisstein Eric W Margin of Error MathWorld
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State




