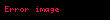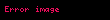Kalkülüs konusu altında bulunan has olmayan integral ya da üvey integral, integralin sınırlarının belli olmaması, yani fonksiyon limitinin , veya belirli bir reel sayı olması ya da iki sınır veya aralarındaki herhangi bir noktada fonksiyonun limitinin sonlu olmaması durumunda oluşur. Sonuca ulaşmak için belirli olmayan sınır noktası kullanılarak fonksiyonun belirli integralinin limiti alınır.


Genellikle şu duruma
ya da şu hale
getirilmeye çalışılır.
Bu sayede içerisinde yatay ya da düşey sonuşmaz bulunan fonksiyonların integralleri alınabilir. Has olmayan integralin ortaya çıkmasının sebebi hesabın temel teoreminin sınırı belli olmayan integrallerde tanımlı olmamasıdır.
| Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kalkulus konusu altinda bulunan has olmayan integral ya da uvey integral integralin sinirlarinin belli olmamasi yani fonksiyon limitinin displaystyle infty displaystyle infty veya belirli bir reel sayi olmasi ya da iki sinir veya aralarindaki herhangi bir noktada fonksiyonun limitinin sonlu olmamasi durumunda olusur Sonuca ulasmak icin belirli olmayan sinir noktasi kullanilarak fonksiyonun belirli integralinin limiti alinir Birinci turden has olmayan bir integral Sinirlari belirtilmemis bir aralikta tanimlanmalidir Ikinci turden bir Riemann integrali Fonksiyonun dikey sonusmazi yuzunden boyle bir integral var olamayabilir Genellikle su duruma limb abf x dx lima abf x dx displaystyle lim b to infty int a b f x mathrm d x qquad lim a to infty int a b f x mathrm d x ya da su hale limc b acf x dx limc a cbf x dx displaystyle lim c to b int a c f x mathrm d x quad lim c to a int c b f x mathrm d x getirilmeye calisilir Bu sayede icerisinde yatay ya da dusey sonusmaz bulunan fonksiyonlarin integralleri alinabilir Has olmayan integralin ortaya cikmasinin sebebi hesabin temel teoreminin siniri belli olmayan integrallerde tanimli olmamasidir Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State