Öklid geometrisinde, bir çift merkezli dörtgen, hem bir hem de çevrel çembere sahip olan bir dörtgendir. Bu çemberlerin çevreleri, yarıçapları ve merkezlerine sırasıyla iç çap (inradius) ve çevrel çap (circumradius), iç merkez (incenter) ve çevrel merkez (circumcenter) denir. Tanımdan, çift merkezli dörtgenlerin hem hem de tüm özelliklerine sahip olduğu anlaşılmaktadır. Bu dörtgenler için diğer isimler kiriş-teğet dörtgeni ve iç teğet ve dış teğet dörtgenidir. Ayrıca nadiren çift çemberli dörtgen ve çift işaretlenmiş dörtgen olarak adlandırılmıştır.

İç içe iki çember, çift merkezli bir dörtgenin iç teğet çemberi ve çevrel çemberiyse, çevrel çemberdeki her nokta, aynı iç teğet çembere ve çevrel çembere sahip çift merkezli bir dörtgenin tepe noktasıdır. Bu, Fransız matematikçi Jean-Victor Poncelet (1788–1867) tarafından kanıtlanan bir sonucudur.
Özel durumlar

Çift merkezli dörtgenlerin örnekleri, kareler, ve ikizkenar .
Tanımlama

 ve temas dörtgen
ve temas dörtgen 
Kenarları 




Diğer üç nitelendirme, kenarlara teğet olduğu noktalarla ilgilidir. Çember, sırasıyla 





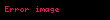


,
'ye diktir.
Bu üçünden ilki, temas dörtgeni WXYZ'nin bir olduğu anlamına gelir.










Başka bir nitelendirmeye göre, eğer 
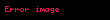


Yine bir başka , teğetler dörtgen 

Çizim

 ile çift merkezli dörtgen
ile çift merkezli dörtgen  . Animasyon için buraya bakın.
. Animasyon için buraya bakın.Çift merkezli bir dörtgen oluşturmak için basit bir yöntem vardır:
Merkez 

























Bu yapının geçerliliği, bir 

Alan
Dört nicelik cinsinden formüller
Çift merkezli bir 





Bu, Brahmagupta formülünün özel bir halidir. Ayrıca bir alanı için trigonometrik formülden doğrudan türetilebilir. Tersinin geçerli olmadığına dikkat edin: Çift merkezli olmayan bazı dörtgenler de 
Alan ayrıca 



İç teğet çemberin merkezi 


Çift merkezli bir dörtgenin 
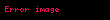


Eğer 
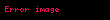


Dörtgen bir ise bu formül kullanılamaz, çünkü bu durumda payda sıfırdır.



burada 
Üç nicelik cinsinden formüller
Çift merkezli bir dörtgenin alanı, iki karşıt kenar ve köşegenler arasındaki 

İki komşu açı ve iç teğet çemberin yarıçapı 
Alan, çevrel çemberin yarıçapı 

burada 




burada 

Eşitsizlikler
Eğer 



Sadece dörtgen bir kare ise her iki taraf için de eşitlik söz konusudur.
Alan için bir başka eşitsizlik ise:p.39,#1203
'dir.
burada 

Alan için bir öncekinden daha keskin bir üst sınır veren benzer bir eşitsizlik ise:
eşitlik ancak ve ancak dörtgen bir ise geçerlidir.
Ek olarak, 




:p.39,#1203
:p.39,#1203
:p.39,#1203
Açı formülleri









Aynı gösterimleri kullanarak, sinüs ve kosinüs fonksiyonları için aşağıdaki formüller geçerlidir:
Köşegenler arasındaki 
İç yarıçap (inradius) ve dış yarıçap (circumradius)
Çift merkezli bir dörtgenin iç teğet çemberinin yarıçapı 




Çevrel çemberin yarıçapı 

İç teğet çemberin yarıçapı, aşağıdaki formüle göre ardışık 



Bu iki formül gerçekte, iç teğet çemberinin yarıçapı 
Çift merkezli bir dörtgenin dört kenarı 



burada 













Çift merkezli bir dörtgen, aynı kenar uzunluk dizisine sahip diğer herhangi bir teğetler dörtgenine göre daha büyük bir yarıçapa sahiptir.:pp.392–393
Eşitsizlikler
Çevrel çemberin yarıçapı 

Bu eşitsizlik, tarafından 1948'de kanıtlanmıştır. Sadece iki çember olduğunda (birbirleriyle aynı merkeze sahip olduklarında) eşitlik geçerli olur; o zaman dörtgen bir karedir. Eşitsizlik, yukarıdaki alan için çifte eşitsizlik kullanılarak birkaç farklı şekilde kanıtlanabilir.
Önceki eşitsizliğin bir uzantısı:p. 141
burada ancak ve ancak her iki tarafta da eşitlik olduğu zaman dörtgen bir karedir.:p. 81
Bir çift merkezli dörtgenin 
burada 

Ayrıca,:p.39,#1203
ve
:p.62,#1599
İç teğet çemberin merkezi (incenter) ve çevrel çemberin merkezi (circumcenter) arasındaki uzunluk

 ve çevrel çemberin merkezi
ve çevrel çemberin merkezi  ile bir ABCD çift merkezli dörtgeni
ile bir ABCD çift merkezli dörtgeniFuss teoremi
Fuss teoremi, herhangi bir çift merkezli dörtgenin yarıçapı 





veya eşdeğer olarak,
1792'de Leonhard Euler'in öğrencisi olan İsviçreli matematikçi (1755–1826) tarafından türetilmiştir. Denklemi 
Üçgenler için Euler teoreminin analogu olan çift merkezli dörtgenler için Fuss teoremi, eğer bir dörtgen çift merkezli ise, iki ilişkili çemberin yukarıdaki denklemlere göre birbiriyle ilişkili olduğunu söyler. Aslında, tersi de geçerlidir: Fuss teoremindeki koşulu sağlayan merkezler arasında 


Fuss teoreminin ifadesinde 




Carlitz özdeşliği
İç teğet çember ve çevrel çemberin merkezleri arasındaki mesafe 
burada 

'dir.
Burada 



Teğet uzunlukları ve kenarlar için eşitsizlikler




ve
burada 






ve
İç teğet çemberin merkezinin diğer özellikleri
Çevrel çemberin merkezi, merkezi ve çift merkezli dörtgenin köşegenlerinin kesişimleri aynı doğru üzerindedir yani .



burada 
Eğer 



Bir çift merkezli dörtgen 



burada 
Köşegenlerin özellikleri
Çift merkezli bir dörtgende köşegenlerin uzunlukları, sırasıyla ve sağlanan formüller olan veya cinsinden ifade edilebilir.
Köşegenleri 


burada 


veya köşegenlerin çarpımı için ikinci dereceden bir denklem olarak çözerek, aşağıdaki biçim elde edilir:
Çift merkezli bir dörtgende 


burada 



Bir çember üzerinde yer alan dört iç teğet çember merkezi






Ayrıca bakınız
Kaynakça
- ^ a b 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover. 1965. ss. 188-193. ISBN .
- ^ a b Yun, Zhang, "Euler's Inequality Revisited", Mathematical Spectrum, Volume 40, Number 3 (May 2008), pp. 119-121. First page available at "Arşivlenmiş kopya" (PDF). 4 Mart 2016 tarihinde kaynağından (PDF). Erişim tarihi: 4 Aralık 2020..
- ^ Geometric Inequalities: In Mathematical Olympiad and Competitions. Şanghay: East China Normal University Press. 2016. s. 22. ISBN .
- ^ Weisstein, Eric W. "Poncelet Transverse." From MathWorld – A Wolfram Web Resource,
- ^ a b c d Characterizations of Bicentric Quadrilaterals (PDF), 10, 2010, ss. 165-173, 31 Aralık 2019 tarihinde kaynağından (PDF), erişim tarihi: 4 Aralık 2020.
- ^ Icons of Mathematics. An exploration of twenty key images. Mathematical Association of America. 2011. ss. 125-126. ISBN .
- ^ a b c Weisstein, Eric, Bicentric Quadrilateral at MathWorld, Accessed on 2011-08-13.
- ^ a b c Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral (PDF), 10, 2010, ss. 119-130, 13 Ağustos 2011 tarihinde kaynağından (PDF), erişim tarihi: 4 Aralık 2020.
- ^ a b c d e f g h The Area of a Bicentric Quadrilateral (PDF), 11, 2011, ss. 155-164, 5 Ocak 2020 tarihinde kaynağından (PDF), erişim tarihi: 4 Aralık 2020.
- ^ a b Durell, C. V. and Robson, A., Advanced Trigonometry, Dover, 2003, pp. 28, 30.
- ^ a b c Yiu, Paul, Euclidean Geometry, 1998, ss. 158-164.
- ^ Lord, Nick, "Quadrilaterals with area formula
", Mathematical Gazette 96, July 2012, 345-347.
- ^ a b c Maximal Area of a Bicentric Quadrilateral (PDF), 12, 2012, ss. 237-241, 23 Nisan 2018 tarihinde kaynağından (PDF), erişim tarihi: 4 Aralık 2020.
- ^ a b When less is more: visualizing basic inequalities. Mathematical Association of America. 2009. ss. 64-66. ISBN .
- ^ a b c d e f Inequalities proposed in , 2007.
- ^ a b A New Proof of Yun’s Inequality for Bicentric Quadrilaterals (PDF), 12, 2012, ss. 79-82, 31 Aralık 2019 tarihinde kaynağından (PDF), erişim tarihi: 4 Aralık 2020.
- ^ M. Radic, Z. Kaliman, and V. Kadum, "A condition that a tangential quadrilateral is also a chordal one", Mathematical Communications, 12 (2007) 33–52.
- ^ Pop, Ovidiu T., "Identities and inequalities in a quadrilateral", Octogon Mathematical Magazine, Vol. 17, No. 2, October 2009, pp 754-763.
- ^ a b c d e f Radic, Mirko, "Certain inequalities concerning bicentric quadrilaterals, hexagons and octagons", Journal of Inequalities in Pure and Applied Mathematics, Volume 6, Issue 1, 2005,
- ^ On a circle containing the incenters of tangential quadrilaterals (PDF), 14, 2014, ss. 389-396, 14 Aralık 2014 tarihinde kaynağından (PDF), erişim tarihi: 4 Aralık 2020.
- ^ Shattuck, Mark, “A Geometric Inequality for Cyclic Quadrilaterals”, Forum Geometricorum 18, 2018, 141-154. http://forumgeom.fau.edu/FG2018volume18/FG201822.pdf 13 Eylül 2018 tarihinde Wayback Machine sitesinde . This paper also gives various inequalities in terms of the arc lengths subtended by a cyclic quadrilateral’s sides.
- ^ Fuss's Theorem, 90 (July), 2006, ss. 306-307.
- ^ The In- and-Circumscribed Quadrilateral, 10, 1909, ss. 123-128, doi:10.2307/1967103.
- ^ Calin, Ovidiu, Euclidean and Non-Euclidean Geometry a metric approach, pp. 153–158.
- ^ Bogomolny, Alex, Collinearity in Bicentric Quadrilaterals, 2004.
- ^ Juan Carlos Salazar, Fuss Theorem for Bicentric Quadrilateral, 2003, .
- ^ 34 (2008) no 4, p. 242.
- ^ . 20 Aralık 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Aralık 2020.
- ^ Alexey A. Zaslavsky, One property of bicentral quadrilaterals, 2019,
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Oklid geometrisinde bir cift merkezli dortgen hem bir hem de cevrel cembere sahip olan bir dortgendir Bu cemberlerin cevreleri yaricaplari ve merkezlerine sirasiyla ic cap inradius ve cevrel cap circumradius ic merkez incenter ve cevrel merkez circumcenter denir Tanimdan cift merkezli dortgenlerin hem hem de tum ozelliklerine sahip oldugu anlasilmaktadir Bu dortgenler icin diger isimler kiris teget dortgeni ve ic teget ve dis teget dortgenidir Ayrica nadiren cift cemberli dortgen ve cift isaretlenmis dortgen olarak adlandirilmistir Cift merkezli dortgenler ABCD displaystyle ABCD ve EFGH displaystyle EFGH icin Poncelet dogal sonucu Ic ice iki cember cift merkezli bir dortgenin ic teget cemberi ve cevrel cemberiyse cevrel cemberdeki her nokta ayni ic teget cembere ve cevrel cembere sahip cift merkezli bir dortgenin tepe noktasidir Bu Fransiz matematikci Jean Victor Poncelet 1788 1867 tarafindan kanitlanan bir sonucudur Ozel durumlarBir dik deltoid Cift merkezli dortgenlerin ornekleri kareler ve ikizkenar TanimlamaCift merkezli dortgen ABCD displaystyle ABCD ve temas dortgen WXYZ displaystyle WXYZ Kenarlari a displaystyle a b displaystyle b c displaystyle c d displaystyle d olan bir disbukey dortgen ABCD displaystyle ABCD ancak ve ancak karsi kenarlar icin ve zit acilarin butunler oldugu ozelligini sagliyorsa cift merkezlidir yani a c b dA C B D p displaystyle begin cases a c b d A C B D pi end cases Diger uc nitelendirme kenarlara teget oldugu noktalarla ilgilidir Cember sirasiyla W displaystyle W X displaystyle X Y displaystyle Y Z displaystyle Z de AB displaystyle AB BC displaystyle BC CD displaystyle CD DA displaystyle DA kenarlarina teget ise tegetler dortgeni ABCD displaystyle ABCD ancak ve ancak asagidaki uc kosuldan herhangi biri gecerliyse ayni zamanda WY displaystyle WY XZ displaystyle XZ ye diktir AWWB DYYC displaystyle frac AW WB frac DY YC ACBD AW CYBX DZ displaystyle frac AC BD frac AW CY BX DZ Bu ucunden ilki temas dortgeni WXYZ nin bir oldugu anlamina gelir E displaystyle E F displaystyle F G displaystyle G H displaystyle H sirasiyla WX displaystyle WX XY displaystyle XY YZ displaystyle YZ ZW displaystyle ZW nin orta noktalari ise tegetler dortgeni ABCD displaystyle ABCD ancak ve ancak EFGH displaystyle EFGH dortgeni bir dikdortgense ayni zamanda kirisler dortgenidir Baska bir nitelendirmeye gore eger I displaystyle I karsit kenarlarin uzantilarinin J displaystyle J ve K displaystyle K de kesistigi bir ic teget cemberin merkezi ise o zaman dortgen de ancak ve ancak JIK displaystyle angle JIK bir dik aci ise kirisler dortgenidir Yine bir baska tegetler dortgen ABCD displaystyle ABCD nin ancak ve ancak temas dortgeni WXYZ displaystyle WXYZ nin Newton dogrusuna dik olmasi durumunda kirisler dortgeni olmasidir Bir dortgenin Newton dogrusu kosegenlerinin orta noktalari tarafindan tanimlanan dogrudur CizimTemas dortgeni WXYZ displaystyle WXYZ ile cift merkezli dortgen ABCD displaystyle ABCD Animasyon icin buraya bakin Cift merkezli bir dortgen olusturmak icin basit bir yontem vardir Merkez I displaystyle I etrafinda r displaystyle r yaricapli Cr displaystyle C r ile baslar ve daha sonra Cr displaystyle C r ic teget cemberi icinde birbirine dik iki WY displaystyle WY ve XZ displaystyle XZ kirisleri cizilir Kirislerin uc noktalarinda ic teget cembere a displaystyle a b displaystyle b c displaystyle c ve d displaystyle d tegetleri cizilir Bunlar cift merkezli bir dortgenin koseleri olan dort A displaystyle A B displaystyle B C displaystyle C ve D displaystyle D noktasinda kesisir Cevrel cemberi cizmek icin cift merkezli dortgen sirasiyla a displaystyle a ve b displaystyle b kenarlarina iki p1 displaystyle p 1 ve p2 displaystyle p 2 cizilir Dikey aciortaylar p1 displaystyle p 1 ve p2 displaystyle p 2 cevrel cember CR displaystyle C R nin merkezi O displaystyle O da ic teget cember Cr displaystyle C r nin merkezi I displaystyle I arasindaki x displaystyle x mesafede kesisir Cevrel cember merkez O displaystyle O etrafinda cizilebilir Bu yapinin gecerliligi bir ABCD displaystyle ABCD de temas dortgeni WXYZ displaystyle WXYZ nin ancak ve ancak ayni zamanda olmasi durumunda dikey kosegenlere sahip oldugu nitelendirmesinden kaynaklanmaktadir AlanDort nicelik cinsinden formuller Cift merkezli bir K displaystyle K dortgeninin alani dortgenin dort niceligiyle kenar uzunluklari birkac farkli sekilde ifade edilebilir Kenarlar a displaystyle a b displaystyle b c displaystyle c d displaystyle d ise alan K abcd displaystyle displaystyle K sqrt abcd Bu Brahmagupta formulunun ozel bir halidir Ayrica bir alani icin trigonometrik formulden dogrudan turetilebilir Tersinin gecerli olmadigina dikkat edin Cift merkezli olmayan bazi dortgenler de K abcd displaystyle displaystyle K sqrt abcd alanina sahiptir Boyle bir dortgene bir ornek kare olmayan bir dikdortgendir Alan ayrica e displaystyle e f displaystyle f g displaystyle g h displaystyle h cinsinden de asagidaki sekilde ifade edilebilir p 128 K efgh4 e f g h displaystyle K sqrt 4 efgh e f g h Ic teget cemberin merkezi I displaystyle I olan cift merkezli dortgen ABCD displaystyle ABCD nin alani icin bir formul asagidaki gibidir K AI CI BI DI displaystyle K AI cdot CI BI cdot DI Cift merkezli bir dortgenin k displaystyle k l displaystyle l ve kosegenleri p displaystyle p q displaystyle q varsa alani asagidaki sekilde ifade edilebilir p 129 K klpqk2 l2 displaystyle K frac klpq k 2 l 2 Eger k displaystyle k l displaystyle l teget kirisleri ve m displaystyle m n displaystyle n dortgenin bimedyanlariysa alan asagidaki formul kullanilarak hesaplanabilir K m2 n2k2 l2 kl displaystyle K left frac m 2 n 2 k 2 l 2 right kl Dortgen bir ise bu formul kullanilamaz cunku bu durumda payda sifirdir M displaystyle M ve N displaystyle N kosegenlerin orta noktalari ve E displaystyle E ve karsit kenarlarin uzantilarinin kesisme noktalari ise cift merkezli bir dortgenin alani su sekilde verilir K 2MN EI FIEF displaystyle K frac 2MN cdot EI cdot FI EF burada I displaystyle I ic teget cemberin merkezidir Uc nicelik cinsinden formuller Cift merkezli bir dortgenin alani iki karsit kenar ve kosegenler arasindaki 8 displaystyle theta acisi cinsinden ifade edilebilir K actan 82 bdcot 82 displaystyle K ac tan frac theta 2 bd cot frac theta 2 Iki komsu aci ve ic teget cemberin yaricapi r displaystyle r cinsinden alan asagidaki formul ile verilmistir K 2r2 1sin A 1sin B displaystyle K 2r 2 left frac 1 sin A frac 1 sin B right Alan cevrel cemberin yaricapi R displaystyle R ve ic teget cemberin yaricapi r displaystyle r cinsinden asagidaki sekilde verilebilir K r r 4R2 r2 sin 8 displaystyle K r r sqrt 4R 2 r 2 sin theta burada 8 displaystyle theta kosegenler arasindaki acidir M displaystyle M ve N displaystyle N kosegenlerin orta noktalari ve E displaystyle E ve F displaystyle F karsit kenarlarin uzantilarinin kesisme noktalari ise alan da su sekilde ifade edilebilir K 2MNEQ FQ displaystyle K 2MN sqrt EQ cdot FQ burada Q displaystyle Q ic teget cemberin merkezinden gecen EF displaystyle EF dogrusuna dik olan ayagidir Esitsizlikler Eger r displaystyle r ve R displaystyle R sirasiyla ic teget cemberin yaricapi ve cevresel cemberin yaricapi ise K displaystyle K alani asagidaki esitsizlikleri saglar 4r2 K 2R2 displaystyle displaystyle 4r 2 leq K leq 2R 2 Sadece dortgen bir kare ise her iki taraf icin de esitlik soz konusudur Alan icin bir baska esitsizlik ise p 39 1203 K 43r4R2 r2 displaystyle K leq tfrac 4 3 r sqrt 4R 2 r 2 dir burada r displaystyle r ve R displaystyle R sirasiyla ic teget cemberin yaricapi ve cevrel cemberin yaricapidir Alan icin bir oncekinden daha keskin bir ust sinir veren benzer bir esitsizlik ise K r r 4R2 r2 displaystyle K leq r r sqrt 4R 2 r 2 dir esitlik ancak ve ancak dortgen bir ise gecerlidir Ek olarak a displaystyle a b displaystyle b c displaystyle c d displaystyle d ve s displaystyle s kenarlari ile 2K s r r2 4R2 displaystyle 2 sqrt K leq s leq r sqrt r 2 4R 2 p 39 12036K ab ac ad bc bd cd 4r2 4R2 4rr2 4R2 displaystyle 6K leq ab ac ad bc bd cd leq 4r 2 4R 2 4r sqrt r 2 4R 2 p 39 12034Kr2 abcd 169r2 r2 4R2 displaystyle 4Kr 2 leq abcd leq frac 16 9 r 2 r 2 4R 2 p 39 1203Aci formulleria displaystyle a b displaystyle b c displaystyle c d displaystyle d sirasiyla AB displaystyle AB BC displaystyle BC CD displaystyle CD DA displaystyle DA cift merkezli dortgenin kenarlarina karsilik gelen uzunluklar ise ABCD displaystyle ABCD tepe acilari tanjant fonksiyonu ile hesaplanabilir tan A2 bcad cot C2 displaystyle tan frac A 2 sqrt frac bc ad cot frac C 2 tan B2 cdab cot D2 displaystyle tan frac B 2 sqrt frac cd ab cot frac D 2 Ayni gosterimleri kullanarak sinus ve kosinus fonksiyonlari icin asagidaki formuller gecerlidir sin A2 bcad bc cos C2 displaystyle sin frac A 2 sqrt frac bc ad bc cos frac C 2 cos A2 adad bc sin C2 displaystyle cos frac A 2 sqrt frac ad ad bc sin frac C 2 sin B2 cdab cd cos D2 displaystyle sin frac B 2 sqrt frac cd ab cd cos frac D 2 cos B2 abab cd sin D2 displaystyle cos frac B 2 sqrt frac ab ab cd sin frac D 2 Kosegenler arasindaki 8 displaystyle theta acisi asagidaki sekilde hesaplanabilir tan 82 bdac displaystyle displaystyle tan frac theta 2 sqrt frac bd ac Ic yaricap inradius ve dis yaricap circumradius Cift merkezli bir dortgenin ic teget cemberinin yaricapi r displaystyle r asagidaki ifadeye gore a displaystyle a b displaystyle b c displaystyle c d displaystyle d kenarlariyla belirlenir r abcda c abcdb d displaystyle displaystyle r frac sqrt abcd a c frac sqrt abcd b d Cevrel cemberin yaricapi R displaystyle R ozel bir durumu olarak asagida verilmistir R 14 ab cd ac bd ad bc abcd displaystyle displaystyle R frac 1 4 sqrt frac ab cd ac bd ad bc abcd Ic teget cemberin yaricapi asagidaki formule gore ardisik e displaystyle e f displaystyle f g displaystyle g h displaystyle h cinsinden de ifade edilebilir p 41 r eg fh displaystyle displaystyle r sqrt eg sqrt fh Bu iki formul gercekte ic teget cemberinin yaricapi r displaystyle r olan bir olmasi icin Cift merkezli bir dortgenin dort kenari a displaystyle a b displaystyle b c displaystyle c d displaystyle d dort cozumudur y4 2sy3 s2 2r2 2r4R2 r2 y2 2rs 4R2 r2 r y r2s2 0 displaystyle y 4 2sy 3 s 2 2r 2 2r sqrt 4R 2 r 2 y 2 2rs sqrt 4R 2 r 2 r y r 2 s 2 0 burada s displaystyle s yari cevre r displaystyle r ve R displaystyle R ise sirasiyla ic teget cemberin yaricapi ve cevrel cemberin yaricapidir p 754 e displaystyle e f displaystyle f g displaystyle g h displaystyle h ve ic teget cemberinin yaricapi r displaystyle r olan cift merkezli bir dortgen varsa teget uzunluklari ev displaystyle e v fv displaystyle f v gv displaystyle g v hv displaystyle h v ve ic teget cemberinin yaricapi rv displaystyle r v olan cift merkezli bir dortgen vardir burada v displaystyle v herhangi bir gercel sayi olabilir pp 9 10 Cift merkezli bir dortgen ayni kenar uzunluk dizisine sahip diger herhangi bir tegetler dortgenine gore daha buyuk bir yaricapa sahiptir pp 392 393 Esitsizlikler Cevrel cemberin yaricapi R displaystyle R ve ic teget cemberin yaricapi r displaystyle r asagidaki esitsizligi saglar R 2r displaystyle R geq sqrt 2 r Bu esitsizlik tarafindan 1948 de kanitlanmistir Sadece iki cember oldugunda birbirleriyle ayni merkeze sahip olduklarinda esitlik gecerli olur o zaman dortgen bir karedir Esitsizlik yukaridaki alan icin cifte esitsizlik kullanilarak birkac farkli sekilde kanitlanabilir Onceki esitsizligin bir uzantisi p 141 r2R 12 sin A2cos B2 sin B2cos C2 sin C2cos D2 sin D2cos A2 1 displaystyle frac r sqrt 2 R leq frac 1 2 left sin frac A 2 cos frac B 2 sin frac B 2 cos frac C 2 sin frac C 2 cos frac D 2 sin frac D 2 cos frac A 2 right leq 1 burada ancak ve ancak her iki tarafta da esitlik oldugu zaman dortgen bir karedir p 81 Bir cift merkezli dortgenin s displaystyle s asagidaki esitsizligi saglar p 13 8r 4R2 r2 r s 4R2 r2 r displaystyle sqrt 8r left sqrt 4R 2 r 2 r right leq s leq sqrt 4R 2 r 2 r burada r displaystyle r ve R displaystyle R sirasiyla ic teget cemberin yaricapi ve cevrel cemberin yaricapidir Ayrica p 39 1203 2sr2 abc abd acd bcd 2r r r2 4R2 2 displaystyle 2sr 2 leq abc abd acd bcd leq 2r r sqrt r 2 4R 2 2 ve abc abd acd bcd 2K K 2R2 displaystyle abc abd acd bcd leq 2 sqrt K K 2R 2 p 62 1599Ic teget cemberin merkezi incenter ve cevrel cemberin merkezi circumcenter arasindaki uzunlukIc teget cemberin merkezi I displaystyle I ve cevrel cemberin merkezi O displaystyle O ile bir ABCD cift merkezli dortgeniFuss teoremi Fuss teoremi herhangi bir cift merkezli dortgenin yaricapi r displaystyle r ve cevrel cemberinin yaricapi R displaystyle R ile merkezi I displaystyle I ve cevrel cemberinin merkezi O displaystyle O arasindaki x displaystyle x uzunlugu arasinda bir iliski verir Bu iliski asagidaki gibi ifade edilebilir 1 R x 2 1 R x 2 1r2 displaystyle frac 1 R x 2 frac 1 R x 2 frac 1 r 2 veya esdeger olarak 2r2 R2 x2 R2 x2 2 displaystyle displaystyle 2r 2 R 2 x 2 R 2 x 2 2 1792 de Leonhard Euler in ogrencisi olan Isvicreli matematikci 1755 1826 tarafindan turetilmistir Denklemi x displaystyle x icin cozersek x R2 r2 r4R2 r2 displaystyle x sqrt R 2 r 2 r sqrt 4R 2 r 2 Ucgenler icin Euler teoreminin analogu olan cift merkezli dortgenler icin Fuss teoremi eger bir dortgen cift merkezli ise iki iliskili cemberin yukaridaki denklemlere gore birbiriyle iliskili oldugunu soyler Aslinda tersi de gecerlidir Fuss teoremindeki kosulu saglayan merkezler arasinda R displaystyle R ve r displaystyle r yaricapli ve iki cemberin merkezleri arasindaki uzaklik x displaystyle x mesafeli iki cember biri digerinin icinde verildiginde bunlardan birini cevreleyen ve digerine iceriden teget olan bir disbukey dortgen vardir ve sonra gore sonsuz sayida vardir Fuss teoreminin ifadesinde x displaystyle x in r displaystyle r ve R displaystyle R cinsinden ifade edilerek x2 0 displaystyle x 2 geq 0 uygulanmasi yukarida belirtilen esitsizligi R 2r displaystyle R geq sqrt 2 r olarak elde etmenin baska bir yoludur Bir genelleme asagidaki sekilde yapilabilir p 5 2r2 x2 R2 2r2 x2 2rx displaystyle 2r 2 x 2 leq R 2 leq 2r 2 x 2 2rx Carlitz ozdesligi Ic teget cember ve cevrel cemberin merkezleri arasindaki mesafe x displaystyle x icin bir baska formul Amerikan matematikci 1907 1999 tarafindan verilmistir Ifade asagidaki gibi yazilir x2 R2 2Rr m displaystyle displaystyle x 2 R 2 2Rr cdot mu burada r displaystyle r ve R displaystyle R sirasiyla ve cevrel cemberin yaricaplari ve m ab cd ad bc a c 2 ac bd ab cd ad bc b d 2 ac bd displaystyle displaystyle mu sqrt frac ab cd ad bc a c 2 ac bd sqrt frac ab cd ad bc b d 2 ac bd dir Burada a displaystyle a b displaystyle b c displaystyle c d displaystyle d cift merkezli dortgenin kenarlaridir Teget uzunluklari ve kenarlar icin esitsizlikler e displaystyle e f displaystyle f g displaystyle g h displaystyle h icin asagidaki esitsizlikler gecerlidir p 3 4r e f g h 4r R2 x2R2 x2 displaystyle 4r leq e f g h leq 4r cdot frac R 2 x 2 R 2 x 2 ve 4r2 e2 f2 g2 h2 4 R2 x2 r2 displaystyle 4r 2 leq e 2 f 2 g 2 h 2 leq 4 R 2 x 2 r 2 burada r displaystyle r ic teget cemberin yaricapi R displaystyle R cevrel cemberin yaricapi ve x displaystyle x ic teget cemberin merkezi ile cevrel cemberin merkezi arasindaki mesafedir a displaystyle a b displaystyle b c displaystyle c d displaystyle d kenarlari asagidaki esitsizlikleri saglar p 5 8r a b c d 8r R2 x2R2 x2 displaystyle 8r leq a b c d leq 8r cdot frac R 2 x 2 R 2 x 2 ve 4 R2 x2 2r2 a2 b2 c2 d2 4 3R2 2r2 displaystyle 4 R 2 x 2 2r 2 leq a 2 b 2 c 2 d 2 leq 4 3R 2 2r 2 Ic teget cemberin merkezinin diger ozellikleriCevrel cemberin merkezi merkezi ve cift merkezli dortgenin kosegenlerinin kesisimleri ayni dogru uzerindedir yani I displaystyle I ic teget cemberin merkezinden bir ABCD displaystyle ABCD cift merkezli dortgeninin dort kosesine olan dort mesafe ile ilgili asagidaki esitlik soz konusudur 1AI2 1CI2 1BI2 1DI2 1r2 displaystyle frac 1 AI 2 frac 1 CI 2 frac 1 BI 2 frac 1 DI 2 frac 1 r 2 burada r displaystyle r ic teget cemberin yaricapidir Eger P displaystyle P ic teget cemberinin merkezi I displaystyle I olan bir cift merkezli dortgen ABCD displaystyle ABCD nin kosegenlerinin kesisme noktasi ise asagidaki esitlik gecerlidir APCP AI2CI2 displaystyle frac AP CP frac AI 2 CI 2 Bir cift merkezli dortgen ABCD displaystyle ABCD icinde ic teget cemberin yaricapi r displaystyle r ve cevrel cemberin yaricapi R displaystyle R ye iliskin bir esitsizlik asagidaki sekilde yazilabilir 4r2 AI CI BI DI 2R2 displaystyle 4r 2 leq AI cdot CI BI cdot DI leq 2R 2 burada I displaystyle I ic teget cemberin merkezidir Kosegenlerin ozellikleriCift merkezli bir dortgende kosegenlerin uzunluklari sirasiyla ve saglanan formuller olan veya cinsinden ifade edilebilir Kosegenleri p displaystyle p ve q displaystyle q olan cift merkezli bir dortgende asagidaki ozdeslik gecerlidir pq4r2 4R2pq 1 displaystyle displaystyle frac pq 4r 2 frac 4R 2 pq 1 burada r displaystyle r ve R displaystyle R sirasiyla ic teget cemberin yaricapi ve cevrel cemberin yaricapidir Bu esitlik asagidaki gibi yeniden yazilabilir r pq2pq 4R2 displaystyle r frac pq 2 sqrt pq 4R 2 veya kosegenlerin carpimi icin ikinci dereceden bir denklem olarak cozerek asagidaki bicim elde edilir pq 2r r 4R2 r2 displaystyle pq 2r left r sqrt 4R 2 r 2 right Cift merkezli bir dortgende p displaystyle p ve q displaystyle q kosegenlerin carpimi icin bir esitsizlik asagidaki gibidir 8pq a b c d 2 displaystyle displaystyle 8pq leq a b c d 2 burada a displaystyle a b displaystyle b c displaystyle c d displaystyle d kenarlardir Bu esitsizlik 1967 de Amerikan matematikci tarafindan kanitlanmistir Bir cember uzerinde yer alan dort ic teget cember merkeziABCD displaystyle ABCD bir cift merkezli dortgen ve O displaystyle O cevrel cemberin merkezi olsun O zaman OAB displaystyle OAB OBC displaystyle OBC OCD displaystyle OCD ODA displaystyle ODA gibi dort ucgenin ic teget cemberlerinin merkezleri bir cember uzerinde yer alir Ayrica bakinizCift merkezli cokgenKaynakca a b 100 Great Problems of Elementary Mathematics Their History and Solutions New York Dover 1965 ss 188 193 ISBN 978 0 486 61348 2 a b Yun Zhang Euler s Inequality Revisited Mathematical Spectrum Volume 40 Number 3 May 2008 pp 119 121 First page available at Arsivlenmis kopya PDF 4 Mart 2016 tarihinde kaynagindan PDF Erisim tarihi 4 Aralik 2020 Geometric Inequalities In Mathematical Olympiad and Competitions Sanghay East China Normal University Press 2016 s 22 ISBN 978 981 4704 13 7 Weisstein Eric W Poncelet Transverse From MathWorld A Wolfram Web Resource a b c d Characterizations of Bicentric Quadrilaterals PDF 10 2010 ss 165 173 31 Aralik 2019 tarihinde kaynagindan PDF erisim tarihi 4 Aralik 2020 Icons of Mathematics An exploration of twenty key images Mathematical Association of America 2011 ss 125 126 ISBN 978 0 88385 352 8 a b c Weisstein Eric Bicentric Quadrilateral at MathWorld Accessed on 2011 08 13 a b c Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral PDF 10 2010 ss 119 130 13 Agustos 2011 tarihinde kaynagindan PDF erisim tarihi 4 Aralik 2020 a b c d e f g h The Area of a Bicentric Quadrilateral PDF 11 2011 ss 155 164 5 Ocak 2020 tarihinde kaynagindan PDF erisim tarihi 4 Aralik 2020 a b Durell C V and Robson A Advanced Trigonometry Dover 2003 pp 28 30 a b c Yiu Paul Euclidean Geometry 1998 ss 158 164 Lord Nick Quadrilaterals with area formula K abcd displaystyle displaystyle K sqrt abcd Mathematical Gazette 96 July 2012 345 347 a b c Maximal Area of a Bicentric Quadrilateral PDF 12 2012 ss 237 241 23 Nisan 2018 tarihinde kaynagindan PDF erisim tarihi 4 Aralik 2020 a b When less is more visualizing basic inequalities Mathematical Association of America 2009 ss 64 66 ISBN 978 0 88385 342 9 a b c d e f Inequalities proposed in 2007 a b A New Proof of Yun s Inequality for Bicentric Quadrilaterals PDF 12 2012 ss 79 82 31 Aralik 2019 tarihinde kaynagindan PDF erisim tarihi 4 Aralik 2020 M Radic Z Kaliman and V Kadum A condition that a tangential quadrilateral is also a chordal one Mathematical Communications 12 2007 33 52 Pop Ovidiu T Identities and inequalities in a quadrilateral Octogon Mathematical Magazine Vol 17 No 2 October 2009 pp 754 763 a b c d e f Radic Mirko Certain inequalities concerning bicentric quadrilaterals hexagons and octagons Journal of Inequalities in Pure and Applied Mathematics Volume 6 Issue 1 2005 On a circle containing the incenters of tangential quadrilaterals PDF 14 2014 ss 389 396 14 Aralik 2014 tarihinde kaynagindan PDF erisim tarihi 4 Aralik 2020 Shattuck Mark A Geometric Inequality for Cyclic Quadrilaterals Forum Geometricorum 18 2018 141 154 http forumgeom fau edu FG2018volume18 FG201822 pdf 13 Eylul 2018 tarihinde Wayback Machine sitesinde This paper also gives various inequalities in terms of the arc lengths subtended by a cyclic quadrilateral s sides Fuss s Theorem 90 July 2006 ss 306 307 The In and Circumscribed Quadrilateral 10 1909 ss 123 128 doi 10 2307 1967103 Calin Ovidiu Euclidean and Non Euclidean Geometry a metric approach pp 153 158 Bogomolny Alex Collinearity in Bicentric Quadrilaterals 2004 Juan Carlos Salazar Fuss Theorem for Bicentric Quadrilateral 2003 34 2008 no 4 p 242 20 Aralik 2022 tarihinde kaynagindan arsivlendi Erisim tarihi 4 Aralik 2020 Alexey A Zaslavsky One property of bicentral quadrilaterals 2019
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State



































