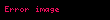Eşoylum eğrisi, eş zamanlı eğri (izokron eğrisi) ya da aynı zamanlı eğri (tautokron eğrisi), birörneklem yerçekimi altında sürtünmesiz olarak kayan bir nesnenin, eğrinin en düşük noktasına ulaşmak için harcadığı sürenin, başlangıç noktasından bağımsız olduğu eğridir. Bu eğri bir sikloiddir ve zaman, sikloidi oluşturan çemberin yarıçapının karekökü ile oranının π katına eşittir. Eşoylum eğrisi, aynı zamanda bir sikloid olan ile ilişkilidir.


Eşoylum eğrisi problemi

Moby Dick - Herman Melville, 1851
Eşoylum eğrisi problemi, bu eğrinin belirlenmesi girişimidir ve 1659'da Christiaan Huygens tarafından çözülmüştür. Huygens, 1673'te ilk kez yayımlanan adlı eserinde geometrik olarak bu eğrinin bir sikloid olduğunu kanıtladı.
| “ | Bir dikey üzerine yerleştirilmiş ekseni olan ve tepe noktası tabanda bulunan bir sikloid üzerinde, herhangi bir noktadan başlayarak tepe noktasındaki en düşük noktaya ulaşan bir cismin iniş süreleri birbirine eşittir... | „ |
Sikloid, yarıçapı 

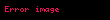
Huygens ayrıca iniş süresinin, sikloidi oluşturan çemberin çapı kadar dikey olarak düşen bir cismin süresine eşit olduğunu ve bunun 



Bu çözüm daha sonra problemini çözmek için kullanılmıştır. Johann Bernoulli, bu problemi bir makalede (, 1697) çözmüştür.

Eşoylum eğrisi problemi, Huygens tarafından daha yakından incelendiğinde, bir sarkaçın dairesel bir yol izlediği için tam olarak olmadığı ve bu nedenle onun sarkacın sallanma genişliğine bağlı olarak farklı zaman tuttuğu fark edilmiştir. Doğru yolu belirledikten sonra, Christiaan Huygens, bob'u asmak için bir ip kullanan ve ipin üst kısmına yakın yerde eşoylum eğrisini oluşturacak kavisli destekler içeren sarkaç saatleri yapmaya çalıştı. Ancak bu girişimler birkaç nedenden dolayı başarısız oldu. İlk olarak, ipin bükülmesi sürtünme yaratıyor ve zamanlamayı değiştiriyordu. İkincisi, eşoylum eğrisi boyunca hareket etmenin sağladığı teorik iyileştirmeleri aşan çok daha önemli zamanlama hatası kaynakları vardı. Son olarak, bir sarkacın "dairesel hatası", salınım uzunluğu azaldıkça küçülür, bu nedenle daha iyi saat bu hatayı önemli ölçüde azaltabilir.
Daha sonra matematikçiler Joseph Louis Lagrange ve Leonhard Euler, bu problemi analitik olarak çözmüşlerdir.
Lagrangian çözümü
(Basit harmonik osilatör), başlangıç noktasından serbest bırakıldığında, ilk yer değiştirmesinden bağımsız olarak, en düşük potansiyel enerji noktasına ulaşma süresi daima periyodunun dörtte birine eşittir ve genlikten bağımsızdır. Bu nedenle, basit harmonik osilatörün Lagrangianı .
Eşoylum eğrisi probleminde, parçacığın konumu en düşük noktadan itibaren s(t) ile parametrize edilirse, kinetik enerji 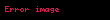
Burada orantı sabiti 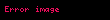
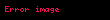


Eğrinin analitik denklemini çözmek için, yukarıdaki ilişkinin diferansiyel formunu göz önünde bulundurun:
Bu denklem, s'yi ortadan kaldırır ve dx ve dh için bir diferansiyel denklem bırakır. Bu, dikey koordinat h'nin tepe noktasından (yatay teğet noktası) değil de noktasından itibaren sayıldığı durumda bir (sikloidin) diferansiyel denklemidir.
Çözümü bulmak için, x'in h üzerinden integralini alın
Burada 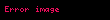
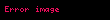
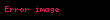
Bu, dikey koordinatın olarak sayıldığı bir sikloidin standart parametrize edilmiş halidir. İlginç olan, yay uzunluğunun karesinin yükseklik farkı ile tam yay uzunluğunun çarpımına (8r) eşit olmasıdır.
Sanal yerçekimi çözümü Tautokron problemine en basit çözüm, eğimin açısı ile parçacığın eğimde hissettiği yerçekimi arasındaki doğrudan ilişkiyi gözlemlemektir. 90° dikey bir eğimdeki bir parçacık tam yerçekimi ivmesi olan 
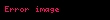


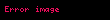

Bir parçacığın eşoylum eğrisi üzerindeki konumu, 
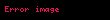
Bu diferansiyel denklem, başlangıç koşulları 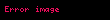
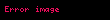
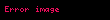
Bu çözümün diferansiyel denklemi sağladığı ve bir parçacığın başlangıç konumu 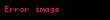

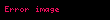
Newton’un ikinci yasası, yerçekimi kuvveti ile parçacığın ivmesi arasındaki ilişkiyi gösterir:
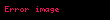

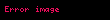
Bu denklem, eğrinin açısındaki değişim ile eğri boyunca olan mesafedeki değişim arasındaki ilişkiyi verir.
Abel'in çözümü
Niels Henrik Abel, tautokron probleminin genelleştirilmiş bir versiyonuna (Abel'in mekanik problemi) saldırdı: Verilen bir yükseklikten toplam düşüş süresini belirten bir fonksiyon olan 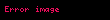
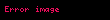
Abel'in çözümü, enerjinin korunumu ilkesine dayanır – parçacık sürtünmesiz olduğu için enerji kaybı yaşamaz ve bu nedenle herhangi bir noktadaki kinetik enerjisi, başlangıç noktasındaki farkına eşittir. Kinetik enerji 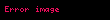
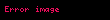



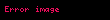

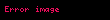
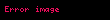
Şimdi parçacığın düşüş süresini bulmak için 

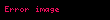
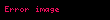
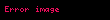
Bu problemi çözmek için, sağdaki integralin bir olduğunu fark ederiz ve her iki tarafın Laplace dönüşümü alınır:

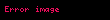
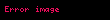
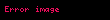
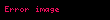
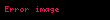
Tautokron problemi için, 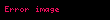
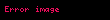
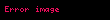

Bu denklemin bir sikloid eğrisini sağladığı gösterilebilir. Eğrinin şekil ifadesini elde etmek için 
Ayrıca bakınız
Kaynakça
Referanslar
- Simmons, George (1972). Diferansiyel Denklemler ve Tarihsel Notlarla Uygulamalar. McGraw–Hill. ISBN .
- Proctor, Richard Anthony (1878). Sikloid ve Sikloidal Eğrilerin Tüm Formları Üzerine Bir İnceleme ve Bu Eğrilerin Gezegenlerin, Kuyruklu Yıldızların ve Güneşten Fırlatılan Maddenin Hareketleriyle İlgisi.
Dış bağlantılar
Mathworld
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Esoylum egrisi es zamanli egri izokron egrisi ya da ayni zamanli egri tautokron egrisi birorneklem yercekimi altinda surtunmesiz olarak kayan bir nesnenin egrinin en dusuk noktasina ulasmak icin harcadigi surenin baslangic noktasindan bagimsiz oldugu egridir Bu egri bir sikloiddir ve zaman sikloidi olusturan cemberin yaricapinin karekoku ile oraninin p katina esittir Esoylum egrisi ayni zamanda bir sikloid olan ile iliskilidir Dort top farkli noktalardan baslayarak bir sikloid egrisi boyunca kayar ancak ayni anda tabana ulasirlar Mavi oklar egri boyunca noktalarin ivmesini gosterir Ustte zaman konum diyagrami yer alir Esoylum egrisini temsil eden nesnelerEsoylum egrisi problemiChristiaan Huygens 1673Pequod un sol taraftaki deneme kabinda sabuntasi etrafimda dikkatle donerken ilk kez dolayli olarak geometriye gore sikloid boyunca kayan tum cisimlerin ornegin benim sabuntasimin herhangi bir noktadan ayni surede inecegi dikkat cekici gercegi tarafindan vuruldum Moby Dick Herman Melville 1851 Esoylum egrisi problemi bu egrinin belirlenmesi girisimidir ve 1659 da Christiaan Huygens tarafindan cozulmustur Huygens 1673 te ilk kez yayimlanan adli eserinde geometrik olarak bu egrinin bir sikloid oldugunu kanitladi Bir dikey uzerine yerlestirilmis ekseni olan ve tepe noktasi tabanda bulunan bir sikloid uzerinde herhangi bir noktadan baslayarak tepe noktasindaki en dusuk noktaya ulasan bir cismin inis sureleri birbirine esittir Sikloid yaricapi r displaystyle r olan bir cemberin x displaystyle x ekseni boyunca yuvarlanirken olusturdugu bir egridir ve asagidaki sekilde verilir x r 8 sin 8 y r 1 cos 8 displaystyle begin aligned x amp r theta sin theta y amp r 1 cos theta end aligned Huygens ayrica inis suresinin sikloidi olusturan cemberin capi kadar dikey olarak dusen bir cismin suresine esit oldugunu ve bunun p 2 displaystyle pi 2 ile carpildigini kanitladi Modern terimlerle bu inis suresinin pr g textstyle pi sqrt r g oldugu anlamina gelir burada r displaystyle r sikloidi olusturan cemberin yaricapi ve g displaystyle g yercekimi ivmesidir Bes esoylum sikloid sarkac farkli genliklerle Bu cozum daha sonra problemini cozmek icin kullanilmistir Johann Bernoulli bu problemi bir makalede 1697 cozmustur Bir semasi Esoylum egrisi problemi Huygens tarafindan daha yakindan incelendiginde bir sarkacin dairesel bir yol izledigi icin tam olarak olmadigi ve bu nedenle onun sarkacin sallanma genisligine bagli olarak farkli zaman tuttugu fark edilmistir Dogru yolu belirledikten sonra Christiaan Huygens bob u asmak icin bir ip kullanan ve ipin ust kismina yakin yerde esoylum egrisini olusturacak kavisli destekler iceren sarkac saatleri yapmaya calisti Ancak bu girisimler birkac nedenden dolayi basarisiz oldu Ilk olarak ipin bukulmesi surtunme yaratiyor ve zamanlamayi degistiriyordu Ikincisi esoylum egrisi boyunca hareket etmenin sagladigi teorik iyilestirmeleri asan cok daha onemli zamanlama hatasi kaynaklari vardi Son olarak bir sarkacin dairesel hatasi salinim uzunlugu azaldikca kuculur bu nedenle daha iyi saat bu hatayi onemli olcude azaltabilir Daha sonra matematikciler Joseph Louis Lagrange ve Leonhard Euler bu problemi analitik olarak cozmuslerdir Lagrangian cozumuBasit harmonik osilator baslangic noktasindan serbest birakildiginda ilk yer degistirmesinden bagimsiz olarak en dusuk potansiyel enerji noktasina ulasma suresi daima periyodunun dortte birine esittir ve genlikten bagimsizdir Bu nedenle basit harmonik osilatorun Lagrangiani Esoylum egrisi probleminde parcacigin konumu en dusuk noktadan itibaren s t ile parametrize edilirse kinetik enerji s 2 displaystyle dot s 2 ile orantilidir ve potansiyel enerji ise yukseklige h s orantilidir Esoylum egrisi problemindeki egrinin es zamanli olmasinin bir yolu Lagrangianin matematiksel olarak basit harmonik osilator ile esdeger olmasidir yani egrinin yuksekligi yay uzunlugunun karesi ile orantili olmalidir h s s28r displaystyle h s frac s 2 8r Burada oranti sabiti 1 8r displaystyle 1 8r dir Basit harmonik osilatorun Lagrangiani ile karsilastirildiginda esdeger yay sabiti k mg 4r displaystyle k mg 4r olur ve inis suresi T 4 p2mk prg displaystyle T 4 frac pi 2 sqrt frac m k pi sqrt frac r g dir Ancak sabit r displaystyle r nin fiziksel anlami egrinin kesin analitik denklemi belirlenene kadar acik degildir Egrinin analitik denklemini cozmek icin yukaridaki iliskinin diferansiyel formunu goz onunde bulundurun dh s ds4r dh2 s2 ds216r2 h dx2 dh2 2r dxdh 2 2rh 1 displaystyle begin aligned dh amp frac s ds 4r dh 2 amp frac s 2 ds 2 16r 2 frac h left dx 2 dh 2 right 2r left frac dx dh right 2 amp frac 2r h 1 end aligned Bu denklem s yi ortadan kaldirir ve dx ve dh icin bir diferansiyel denklem birakir Bu dikey koordinat h nin tepe noktasindan yatay teget noktasi degil de noktasindan itibaren sayildigi durumda bir sikloidin diferansiyel denklemidir Cozumu bulmak icin x in h uzerinden integralini alin dxdh 2r hh x 4r 1 u2 du displaystyle begin aligned frac dx dh amp frac sqrt 2r h sqrt h x amp 4r int sqrt 1 u 2 du end aligned Burada u h 2r displaystyle u sqrt h 2r ve yukseklik azalirken parcacik ileri hareket eder dx dh lt 0 displaystyle dx dh lt 0 Bu integral bir cemberin altindaki alandir ve bir baska donusum olan u cos t 2 displaystyle u cos t 2 ile yapilabilir ve sonuc olarak su ifadeye ulasilir x r t sin t h r 1 cos t displaystyle begin aligned x amp r t sin t h amp r 1 cos t end aligned Bu dikey koordinatin olarak sayildigi bir sikloidin standart parametrize edilmis halidir Ilginc olan yay uzunlugunun karesinin yukseklik farki ile tam yay uzunlugunun carpimina 8r esit olmasidir Sanal yercekimi cozumu Tautokron problemine en basit cozum egimin acisi ile parcacigin egimde hissettigi yercekimi arasindaki dogrudan iliskiyi gozlemlemektir 90 dikey bir egimdeki bir parcacik tam yercekimi ivmesi olan g displaystyle g yi deneyimlerken yatay bir duzlemdeki parcacik sifir yercekimi ivmesi hisseder Ara acilarda ise parcacigin sanal yercekimi nedeniyle yasadigi ivme gsin 8 displaystyle g sin theta olur Burada 8 displaystyle theta egriye teget olan dogru ile yatay arasindaki aci olarak olculur ve yatayin uzerindeki acilar pozitif kabul edilir Bu nedenle 8 displaystyle theta acisi p 2 displaystyle pi 2 ile p 2 displaystyle pi 2 arasinda degisir Bir parcacigin esoylum egrisi uzerindeki konumu s t displaystyle s t asagidaki diferansiyel denklemi saglamalidir d2sdt2 w2s displaystyle frac d 2 s dt 2 omega 2 s Bu diferansiyel denklem baslangic kosullari s 0 s0 displaystyle s 0 s 0 ve s 0 0 displaystyle s 0 0 ile birlikte su cozumu verir s t s0cos wt displaystyle s t s 0 cos omega t Bu cozumun diferansiyel denklemi sagladigi ve bir parcacigin baslangic konumu s0 displaystyle s 0 dan s 0 displaystyle s 0 noktasina p 2w displaystyle pi 2 omega surede ulastigi kolayca dogrulanabilir Problem simdi parcacigin yukaridaki hareketi takip etmesini saglayacak bir egri olusturmaktir Newton un ikinci yasasi yercekimi kuvveti ile parcacigin ivmesi arasindaki iliskiyi gosterir gsin 8 d2sdt2 w2s displaystyle begin aligned g sin theta amp frac d 2 s dt 2 amp omega 2 s end aligned Bu denklemin acikca mesafeyi s displaystyle s icermesi karmasiktir ancak daha yonetilebilir bir forma donusturmek icin turev alinabilir gcos 8 d8 w2 ds ds gw2cos 8 d8 displaystyle begin aligned g cos theta d theta amp omega 2 ds Longrightarrow ds amp frac g omega 2 cos theta d theta end aligned Bu denklem egrinin acisindaki degisim ile egri boyunca olan mesafedeki degisim arasindaki iliskiyi verir Abel in cozumuNiels Henrik Abel tautokron probleminin genellestirilmis bir versiyonuna Abel in mekanik problemi saldirdi Verilen bir yukseklikten toplam dusus suresini belirten bir fonksiyon olan T y displaystyle T y verildiginde bu sonucu elde eden egrinin denklemini bulmak Tautokron problemi T y displaystyle T y sabit oldugunda Abel in mekanik probleminin ozel bir durumudur Abel in cozumu enerjinin korunumu ilkesine dayanir parcacik surtunmesiz oldugu icin enerji kaybi yasamaz ve bu nedenle herhangi bir noktadaki kinetik enerjisi baslangic noktasindaki farkina esittir Kinetik enerji 12mv2 textstyle frac 1 2 mv 2 seklindedir ve parcacik bir egri boyunca hareket ettigi icin hizi basitce dℓ dt displaystyle d ell dt seklinde ifade edilir burada ℓ displaystyle ell egri boyunca olculen mesafedir Benzer sekilde bir baslangic yuksekligi y0 displaystyle y 0 dan bir yukseklik y displaystyle y ye duserken kazanilan yercekimsel potansiyel enerji mg y0 y displaystyle mg y 0 y seklindedir Boylece 12m dℓdt 2 mg y0 y dℓdt 2g y0 y dt dℓ2g y0 y dt 12g y0 y dℓdydy displaystyle begin aligned frac 1 2 m left frac d ell dt right 2 amp mg y 0 y frac d ell dt amp pm sqrt 2g y 0 y dt amp pm frac d ell sqrt 2g y 0 y dt amp frac 1 sqrt 2g y 0 y frac d ell dy dy end aligned Son denklemde kalan mesafeyi yukseklik fonksiyonu olarak yazmak icin ℓ y displaystyle ell y kullanilmis mesafenin zamanla azaldigi eksi isareti varsayilmis ve zincir kurali su sekilde uygulanmistir dℓ dℓdy dy textstyle d ell frac d ell dy dy Simdi parcacigin dusus suresini bulmak icin y y0 displaystyle y y 0 noktasindan y 0 displaystyle y 0 noktasina kadar integrasyon yapilir T y0 y y0y 0dt 12g 0y01y0 ydℓdydy displaystyle T y 0 int y y 0 y 0 dt frac 1 sqrt 2g int 0 y 0 frac 1 sqrt y 0 y frac d ell dy dy Bu denklem Abel in integral denklemi olarak adlandirilir ve verilen bir egri boyunca bir parcacigin dusme suresini hesaplamak icin kullanilir Ancak Abel in mekanik problemi tersini gerektirir T y0 displaystyle T y 0 verildiginde f y dℓ dy displaystyle f y d ell dy yi bulmamiz gerekir Bu problemi cozmek icin sagdaki integralin bir oldugunu fark ederiz ve her iki tarafin Laplace donusumu alinir L T y0 12gL 1y F s displaystyle mathcal L T y 0 frac 1 sqrt 2g mathcal L left frac 1 sqrt y right F s Burada F s L dℓ dy displaystyle F s mathcal L left d ell dy right Cunku L 1 y p s textstyle mathcal L left 1 sqrt y right sqrt pi s oldugundan L dℓdy 2gps12L T y0 displaystyle mathcal L left frac d ell dy right sqrt frac 2g pi s frac 1 2 mathcal L T y 0 Bu noktadan sonra T y0 displaystyle T y 0 i belirledikten sonra onun Laplace donusumunu hesaplayabiliriz ve dℓ dy displaystyle d ell dy nin Laplace donusumunu bulabiliriz Tautokron problemi icin T y0 T0 displaystyle T y 0 T 0 sabittir 1 in Laplace donusumu 1 s displaystyle 1 s oldugundan F s 2gpT0s 12 displaystyle F s sqrt frac 2g pi T 0 s frac 1 2 Yine yukaridaki Laplace donusumunu kullanarak donusumu ters cevirir ve su sonuca variriz dℓdy T02gp1y displaystyle frac d ell dy T 0 frac sqrt 2g pi frac 1 sqrt y Bu denklemin bir sikloid egrisini sagladigi gosterilebilir Egrinin sekil ifadesini elde etmek icin y displaystyle y ye gore integral alinmalidir Ayrica bakinizKaynakca Blackwell Richard J 1986 Christiaan Huygens The Pendulum Clock Part II Proposition XXV s 69 Iowa State University Press ISBN 0 8138 0933 9 ReferanslarSimmons George 1972 Diferansiyel Denklemler ve Tarihsel Notlarla Uygulamalar McGraw Hill ISBN 0 07 057540 1 Proctor Richard Anthony 1878 Sikloid ve Sikloidal Egrilerin Tum Formlari Uzerine Bir Inceleme ve Bu Egrilerin Gezegenlerin Kuyruklu Yildizlarin ve Gunesten Firlatilan Maddenin Hareketleriyle Ilgisi Dis baglantilarMathworld
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State