Öz direnç (Empedans), maddenin kimyasal özelliğinden dolayı direncinin artması ya da azalmasına neden olan her maddeye özgü ayırt edici bir özelliktir. Farklı maddelerin empedansları aynı olabilir ama öz dirençleri aynı olamaz. R= Lq/Q dur. (Rezistif Direnç= Uzunluk*öz direnç/kesit, (empedans ya da elektriksel empedans olarak da adlandırılır) Alternatif akım'a (İngilizce'de AC) karşı koyan zorluk olarak adlandırılır. İçinde kondansatör ve endüktans gibi zamanla değişen değerlere sahip olan elemanlar olan devrelerde direnç yerine öz direnç kullanılmaktadır. Öz direnç gerilim ve akımın sadece görünür genliğini açıklamakla kalmaz, ayrıca görünür fazını da açıklar. DA (DC) devrelerinde öz direnç ile direnç arasında hiçbir fark yoktur. Direnç sıfır faz açısına sahip öz direnç olarak adlandırılabilir.

Öz direncin genellikle sembolü ile gösterilir ve hem genliğini hem de fazını ifade eden gösterim 'dir. Bununla beraber karmaşık sayı ifadesi devre analizi uygulamalarında daha sık kullanılır. Empedans (öz direnç) ifadesi ilk olarak Temmuz 1886'da Oliver Heaviside tarafından kullanıldı. 1893'te de öz direnci karmaşık sayılarla ilk kullanandı.
Öz direnç, gerilimin akıma bölümüdür. Diğer ifadeyse, gerilim–akım oranı belirli ω sıklıktaki tek bir karmaşık kuvvettir. Öz direnç genellikle karmaşık sayıdır. Fakat bu karmaşık sayı, Uluslararası Birimler Sistemi (SI)'ya göre direnç ile aynı birime sahiptir ve o da ohm'dur. Sinüzoid bir akım veya gerilim için, Karmaşık öz direncin (kutupsal form), gerilim ve akımın genlik ve fazını ifade eder. Özellikle,
- Karmaşık öz direncin genliği, voltaj genliğinin akımın genliğine oranıdır.
- Karmaşık öz direncin fazı, akımla gerilim arasındaki faz farkıdır.
Empedansın çarpmaya göre tersi admittanstır (örn, admittans akımın gerilime oranıdır ve siemens olarak bilinir. Eskiden birimi mho idi.)
Karmaşık öz direnç
Öz direnç bir karmaşık büyüklük ile ifade edilir 
Burada 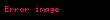


Burada öz direncin, gerçel kısmı 
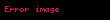
Öz direnci daha uygun yapmak için kartezyen formuna ekleyip çıkartmak gerekir. Çarpma veya bölme gibi işlemlerde kutupsal form kullanılmak daha basittir. Bir devrede iki paralel öz direnç arasındaki toplam öz direnci bulmak için, hesaplamada formları birkaç kez birbirine dönüştürmek gerekebilir. Formların dönüşümü için normal (karmaşık sayıların dönüşüm kuralları) uygulanır.
Ohm kanunu

 yüküne paralel bağlı gerilim kaynağı
yüküne paralel bağlı gerilim kaynağı  ve aynı yüke seri bağlı bir akım kaynağı
ve aynı yüke seri bağlı bir akım kaynağı  .
.Öz direncin anlamı Ohm kanununda daha iyi anlaşılabilir.
Öz direncin büyüklüğü 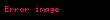




Ohm kanunlarını AA devrelerine uygulayarak öz direnç genişletilir. , , Thevenin teoremi ve Norton Teoremi gibi DA (DC) devre analizindeki diğer sonuçlar da AA devrelerine, direnç yerine öz direnç konularak uygulanabilir.
Karmaşık gerilim ve akım

Hesaplamaları basitleştirmek için, sinüzoidal gerilim ve akım dalgaları, yaygın olarak karmaşık değerli fonksiyonlar şu şekilde ifade edilir: 

Öz direnç, yukarıdaki niceliklerin oranı olarak tanımlanır.
Bunları Ohm kanununa uygularsak;
Bu, tüm 
Büyüklük eşitliği, Ohm kanununun gerilim ve akım genliklerine uygulanmış haline benzerken ikinci eşitlik faz ilişkisini açıklar.
Karmaşık ifadenin geçerliliği
Karmaşık üs kullanılarak yukarıdaki ifade şu şekle dönüştürülebilir (Euler formülüne göre):
örn, gerçek değerli sinüzoidal fonksiyon (bizim gerilim ve akım dalgasını ifade eder), iki karmaşık değerli fonksiyona ayrılabilir. Süperpozisyon ilkesine göre, sol taraftaki sinüzoidin davranışını, sağ taraftaki gibi iki karmaşık terimin davranışı gibi ayırarak analiz edebiliriz. Sadece sağ taraftaki bir terimin analizi gerçekleştirme bize diğeri için de benzer sonuç verecektir. Herhangi bir hesaplama sonunda, gerçel değerli sinüzoidleri şu ifade de yerine koyabiliriz:
Diğer ifadeyse, basitçe sonucun gercel kısmı elde edilir.
Fazörler
Fazör, genellikle üstel formda ifade edilen sabit bir karmaşık sayıdır. Zamanın sinüzoidal fonksiyonunun karmaşık genliğini belirtir. Fazörler, sinüzoidlerin bulunduğu hesaplamaları basitleştirmek için elektrik mühendisleri tarafından kullanılırlar. Diferansiyel eşitliği cebirsel ifadeye dönüştürmek için kullanılırlar.
Bir devre elemanı olan öz direnç, fazör gerilim elemanının, fazör akım elemanına oranı olarak tanımlanabilirken ayrıca göreceli olarak gerilim ve akımın genliğini ve fazını da ifade eder. Buradaki fazör, yukarıda verilen Ohm kanunundaki 
Aygıtsal örnekler

 kadarlık bir farkla takip ederken, bobinin gerilimi ise akımını
kadarlık bir farkla takip ederken, bobinin gerilimi ise akımını  kadarlık bir farkla takip ediyor. Özdeş gerilim ve akım genlikleri, her birinin öz dirençlerinin büyüklüklerinin birbirine eşit olduğunu gösteriyor.
kadarlık bir farkla takip ediyor. Özdeş gerilim ve akım genlikleri, her birinin öz dirençlerinin büyüklüklerinin birbirine eşit olduğunu gösteriyor.İdeal bir direncin empedansı tamamen gerçeldir ve rezistif empedans olarak ifade edilir:
İdeal bobinler ve kondansatörler tam sanal reaktif empedansa sahiptirler:
Aşağıdaki öşdeşlikler sanal birim ve onun karşıtları içindir:
Buradan bobin ve kondansatörün empedanslarını kutupsal formda şöyle yazabiliriz:
Büyüklük, belirli bir akım genliği için, öz dirençteki, gerilimin genliğinin değişmesi, üstel faktörlerin faz ilişkisini verir.
Aygıta özgü öz direç türetme
Aşağıda, üç temel devre elemanı olan direnç, kondansatör ve bobin'in öz dirençlerinin türetilmesi gösteriliyor. Herhangi rastgele gerilim ve akımı arasındaki ilişkiyi tanımlamak için, bu türetimlerde her rastgele sinyalin, Fourier analiziyle sinüzoidlerin toplamına yaklaşık olduğunda, sinüzoidal sinyaller varsayılacak.
Direnç
Direnç için şöyle bir ilişki vardır:
Bu, Ohm kanununun basit ifadesidir.
Gerilim sinyaline göre,
olur.
Buradan
Bu, AA (AC) gerilim genliğinin, AA akım genliğine oranının 
Bu sonuç genellikle şu biçimde kısaltılır:
Kondansatör
Konsansatör için ise şöyle bir ilişki vardır:
Gerilim sinyaline göre
olur.
Buradan
Sonrasında
Bu, AA (AC) gerilim genliğinin, AA akım genliğine oranının 
Bu sonuç genellikle (kutupsal formda) şöyle kısaltılır;
veya Euler formülünü uygulayarak;
Bobin
Bobin için şöyle ilişki vardır:
Bu sefer akım sinyaline göre
olur
Buradan,
Sonrasında,
Bu, AA (AC) gerilim genliğinin, AA akım genliğine oranının 
Bu sonuç kutupsal forma genellikle şöyle kısaltılabilir; :
Veya daha basit olarak Euler formülü kullanılarak; :
Resistans ve reaktans
Direnç ve reaktans öz direncin genlik ve fazını birlikte şu şekilde ifade ederler:
Birçok uygulamada gerilim ve akımın göreceli fazı, çok da önemli olmadığında, sadece öz direncin genliği önemlidir.
Direnç
Direnç 
Reaktans
Reaktans 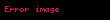

Tam reaktif bileşeninde, sinüzoidal gerilim, akımın tam çeyrek evre farkladır. Bu, bileşenin, devredeki enerjiyi çektiği ve sonra tekrar devreye geri verdiği anlamına gelir Saf reaktans hiçbir güç harcamaz.
Kapasitif reaktans
Kondansatör tam reaktif empedansa sahiptir, o da sinyal frekansı ile (ters orantılıdır). Kondansatör, bir yalıtkanla (dielektrik olarak da bilinir) ayrılan iki iletkenden oluşur.
Düşük frekanslarda kondansatör ve yalıtkandan akan yük yoktur...
İndüktif reaktans
İndüktif reaktans 


Bobin iletken sargılardan oluşur. Elektromanyetik indükleme, Faraday yasasına göre, 


Geri emk, akan akımın karşısındaki kaynaktır. Sabit doğru akımda sıfır yük vardır ve bobin kısa devre gibi gözükür. Alternatif akım ortalama bir zamanda yüke sahiptir ve frekansla orantılıdır. Bundan dolayıdır ki indüktif reaktans frekansla artar.
Ayrıca bakınız
Kaynakça
- ^ Science, p. 18, 1888
- ^ Oliver Heaviside, Elektrikçi, p. 212, 23 Temmuz 1886'da Elektriksel sayfalara yazıldı, p64, AMS Bookstore,
- ^ Kennelly, Arthur. Öz direnç (IEEE, 1893)
- ^ AC Ohm's law 19 Şubat 2011 tarihinde Wayback Machine sitesinde ., Hyperphysics
- ^ Horowitz, Paul (1989). "1". The Art of Electronics. Cambridge University Press. ss. 32-33. ISBN .
- ^ Capacitor/inductor phase relationships 3 Ağustos 2008 tarihinde Wayback Machine sitesinde ., Yokogawa
- ^ Complex impedance 19 Temmuz 2010 tarihinde Wayback Machine sitesinde ., Hyperphysics
- ^ Horowitz, Paul (1989). "1". The Art of Electronics. Cambridge University Press. ss. 31-32. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Oz direnc Empedans maddenin kimyasal ozelliginden dolayi direncinin artmasi ya da azalmasina neden olan her maddeye ozgu ayirt edici bir ozelliktir Farkli maddelerin empedanslari ayni olabilir ama oz direncleri ayni olamaz R Lq Q dur Rezistif Direnc Uzunluk oz direnc kesit empedans ya da elektriksel empedans olarak da adlandirilir Alternatif akim a Ingilizce de AC karsi koyan zorluk olarak adlandirilir Icinde kondansator ve enduktans gibi zamanla degisen degerlere sahip olan elemanlar olan devrelerde direnc yerine oz direnc kullanilmaktadir Oz direnc gerilim ve akimin sadece gorunur genligini aciklamakla kalmaz ayrica gorunur fazini da aciklar DA DC devrelerinde oz direnc ile direnc arasinda hicbir fark yoktur Direnc sifir faz acisina sahip oz direnc olarak adlandirilabilir Oz direncin grafiksel gosterimi Oz direncin genellikle Z displaystyle scriptstyle Z sembolu ile gosterilir ve hem genligini hem de fazini ifade eden gosterim Z 8 displaystyle scriptstyle Z angle theta dir Bununla beraber karmasik sayi ifadesi devre analizi uygulamalarinda daha sik kullanilir Empedans oz direnc ifadesi ilk olarak Temmuz 1886 da Oliver Heaviside tarafindan kullanildi 1893 te de oz direnci karmasik sayilarla ilk kullanandi Oz direnc gerilimin akima bolumudur Diger ifadeyse gerilim akim orani belirli w sikliktaki tek bir karmasik kuvvettir Oz direnc genellikle karmasik sayidir Fakat bu karmasik sayi Uluslararasi Birimler Sistemi SI ya gore direnc ile ayni birime sahiptir ve o da ohm dur Sinuzoid bir akim veya gerilim icin Karmasik oz direncin kutupsal form gerilim ve akimin genlik ve fazini ifade eder Ozellikle Karmasik oz direncin genligi voltaj genliginin akimin genligine oranidir Karmasik oz direncin fazi akimla gerilim arasindaki faz farkidir Empedansin carpmaya gore tersi admittanstir orn admittans akimin gerilime oranidir ve siemens olarak bilinir Eskiden birimi mho idi Karmasik oz direncOz direnc bir karmasik buyukluk ile ifade edilir Z displaystyle scriptstyle Z ve karmasik oz direnc ifadesi de kullanilabilir Kutupsal form hem genligi hem de faz karakteristiklerini uygun olarak karsiliyor Z Z ei8 displaystyle Z Z e i theta quad Burada Z displaystyle scriptstyle Z buyuklugu gerilim fark genliginin akim fark genligine oranidiyken 8 displaystyle scriptstyle theta degiskeni gerilim ile akim arasindaki faz farkini verir ve i displaystyle scriptstyle i sanal kisimdir Kartezyen formunda Z R iX displaystyle Z R iX quad Burada oz direncin gercel kismi R displaystyle scriptstyle R resistans direncini ve sanal kismi da X displaystyle scriptstyle X reaktansini verir Oz direnci daha uygun yapmak icin kartezyen formuna ekleyip cikartmak gerekir Carpma veya bolme gibi islemlerde kutupsal form kullanilmak daha basittir Bir devrede iki paralel oz direnc arasindaki toplam oz direnci bulmak icin hesaplamada formlari birkac kez birbirine donusturmek gerekebilir Formlarin donusumu icin normal karmasik sayilarin donusum kurallari uygulanir Ohm kanunuBir AA devresinde Z displaystyle scriptstyle Z yukune paralel bagli gerilim kaynagi V displaystyle scriptstyle V ve ayni yuke seri bagli bir akim kaynagi I displaystyle scriptstyle I Oz direncin anlami Ohm kanununda daha iyi anlasilabilir V IZ I Z ej8 displaystyle V IZ I Z e j theta quad Oz direncin buyuklugu Z displaystyle scriptstyle Z belirli bir direnc gibidir Belirli bir I displaystyle scriptstyle I akimi altinda Z displaystyle scriptstyle Z oz direncine karsi gerilimin siddetidir Faz faktoru 8 displaystyle scriptstyle theta fazina gore akimin gerilimden geri kaldigini soyler orn akim sinyali gerilim sinyali istegi uzerine o ana gore 82pT displaystyle scriptstyle frac theta 2 pi T kadar degistirildi Ohm kanunlarini AA devrelerine uygulayarak oz direnc genisletilir Thevenin teoremi ve Norton Teoremi gibi DA DC devre analizindeki diger sonuclar da AA devrelerine direnc yerine oz direnc konularak uygulanabilir Karmasik gerilim ve akimBir devredeki toplam oz direnc direnc sembolu ile ayni sekilde US ANSI veya DIN Avro veya etiketli bir kutu seklinde cizilebilir Hesaplamalari basitlestirmek icin sinuzoidal gerilim ve akim dalgalari yaygin olarak karmasik degerli fonksiyonlar su sekilde ifade edilir V displaystyle scriptstyle V ve I displaystyle scriptstyle I V V ej wt ϕV displaystyle V V e j omega t phi V I I ej wt ϕI displaystyle I I e j omega t phi I Oz direnc yukaridaki niceliklerin orani olarak tanimlanir Z VI displaystyle Z frac V I Bunlari Ohm kanununa uygularsak V ej wt ϕV I ej wt ϕI Z ej8 I Z ej wt ϕI 8 displaystyle begin aligned V e j omega t phi V amp I e j omega t phi I Z e j theta amp I Z e j omega t phi I theta end aligned Bu tum t displaystyle t ler icin gecerlidir Buyukluk ve fazi su sekilde esitleyebiliriz V I Z displaystyle V I Z quad ϕV ϕI 8 displaystyle phi V phi I theta quad Buyukluk esitligi Ohm kanununun gerilim ve akim genliklerine uygulanmis haline benzerken ikinci esitlik faz iliskisini aciklar Karmasik ifadenin gecerliligi Karmasik us kullanilarak yukaridaki ifade su sekle donusturulebilir Euler formulune gore cos wt ϕ 12 ej wt ϕ e j wt ϕ displaystyle cos omega t phi frac 1 2 Big e j omega t phi e j omega t phi Big orn gercek degerli sinuzoidal fonksiyon bizim gerilim ve akim dalgasini ifade eder iki karmasik degerli fonksiyona ayrilabilir Superpozisyon ilkesine gore sol taraftaki sinuzoidin davranisini sag taraftaki gibi iki karmasik terimin davranisi gibi ayirarak analiz edebiliriz Sadece sag taraftaki bir terimin analizi gerceklestirme bize digeri icin de benzer sonuc verecektir Herhangi bir hesaplama sonunda gercel degerli sinuzoidleri su ifade de yerine koyabiliriz cos wt ϕ ℜ ej wt ϕ displaystyle cos omega t phi Re Big e j omega t phi Big Diger ifadeyse basitce sonucun gercel kismi elde edilir Fazorler Fazor genellikle ustel formda ifade edilen sabit bir karmasik sayidir Zamanin sinuzoidal fonksiyonunun karmasik genligini belirtir Fazorler sinuzoidlerin bulundugu hesaplamalari basitlestirmek icin elektrik muhendisleri tarafindan kullanilirlar Diferansiyel esitligi cebirsel ifadeye donusturmek icin kullanilirlar Bir devre elemani olan oz direnc fazor gerilim elemaninin fazor akim elemanina orani olarak tanimlanabilirken ayrica goreceli olarak gerilim ve akimin genligini ve fazini da ifade eder Buradaki fazor yukarida verilen Ohm kanunundaki ejwt displaystyle scriptstyle e j omega t ifadesidir Aygitsal orneklerEsitliklerde bobin ve kondansatorlerin oz direncinin faz acilari goruluyor Kondansatorun gerilimi akimini p 2 displaystyle pi 2 kadarlik bir farkla takip ederken bobinin gerilimi ise akimini p 2 displaystyle pi 2 kadarlik bir farkla takip ediyor Ozdes gerilim ve akim genlikleri her birinin oz direnclerinin buyukluklerinin birbirine esit oldugunu gosteriyor Ideal bir direncin empedansi tamamen gerceldir ve rezistif empedans olarak ifade edilir ZR R displaystyle Z R R Ideal bobinler ve kondansatorler tam sanal reaktif empedansa sahiptirler ZL jwL displaystyle Z L j omega L ZC 1jwC displaystyle Z C frac 1 j omega C Asagidaki osdeslikler sanal birim ve onun karsitlari icindir j cos p2 jsin p2 ejp2 displaystyle j cos left frac pi 2 right j sin left frac pi 2 right e j frac pi 2 1j j cos p2 jsin p2 ej p2 displaystyle frac 1 j j cos left frac pi 2 right j sin left frac pi 2 right e j frac pi 2 Buradan bobin ve kondansatorun empedanslarini kutupsal formda soyle yazabiliriz ZL wLejp2 displaystyle Z L omega Le j frac pi 2 ZC 1wCej p2 displaystyle Z C frac 1 omega C e j frac pi 2 Buyukluk belirli bir akim genligi icin oz direncteki gerilimin genliginin degismesi ustel faktorlerin faz iliskisini verir Aygita ozgu oz direc turetme Asagida uc temel devre elemani olan direnc kondansator ve bobin in oz direnclerinin turetilmesi gosteriliyor Herhangi rastgele gerilim ve akimi arasindaki iliskiyi tanimlamak icin bu turetimlerde her rastgele sinyalin Fourier analiziyle sinuzoidlerin toplamina yaklasik oldugunda sinuzoidal sinyaller varsayilacak Direnc Direnc icin soyle bir iliski vardir vR t iR t R displaystyle v text R left t right i text R left t right R Bu Ohm kanununun basit ifadesidir Gerilim sinyaline gore vR t Vpsin wt displaystyle v text R t V p sin omega t olur Buradan vR t iR t Vpsin wt Ipsin wt R displaystyle frac v text R left t right i text R left t right frac V p sin omega t I p sin left omega t right R Bu AA AC gerilim genliginin AA akim genligine oraninin R displaystyle scriptstyle R gibi bir direnc oldugunu gosteriyor ve AA gerilimini AA akiminin 0 dereceyle takip eden bir direnc oldugunu soyluyor Bu sonuc genellikle su bicimde kisaltilir Zdirenc R displaystyle Z text direnc R Kondansator Konsansator icin ise soyle bir iliski vardir iC t Cd vC t d t displaystyle i text C t C frac operatorname d v text C t operatorname d t Gerilim sinyaline gore vC t Vpsin wt displaystyle v text C t V p sin omega t olur Buradan d vC t d t wVpcos wt displaystyle frac operatorname d v text C t operatorname d t omega V p cos left omega t right Sonrasinda vC t iC t Vpsin wt wVpCcos wt sin wt wCsin wt p2 displaystyle frac v text C left t right i text C left t right frac V p sin omega t omega V p C cos left omega t right frac sin omega t omega C sin left omega t frac pi 2 right Bu AA AC gerilim genliginin AA akim genligine oraninin 1wC displaystyle scriptstyle frac 1 omega C gibi bir kondansator oldugunu gosteriyor ve AA gerilimini AA akimini 90 dereceyle takip eden bir kondansator oldugunu soyluyor Bu sonuc genellikle kutupsal formda soyle kisaltilir Zkondansator 1wCe jp2 displaystyle Z text kondansator frac 1 omega C e j frac pi 2 veya Euler formulunu uygulayarak Zkondansator j1wC 1jwC displaystyle Z text kondansator j frac 1 omega C frac 1 j omega C Bobin Bobin icin soyle iliski vardir vL t Ld iL t d t displaystyle v text L t L frac operatorname d i text L t operatorname d t Bu sefer akim sinyaline gore iL t Ipsin wt displaystyle i text L t I p sin omega t olur Buradan d iL t d t wIpcos wt displaystyle frac operatorname d i text L t operatorname d t omega I p cos left omega t right Sonrasinda vL t iL t wIpLcos wt Ipsin wt wLsin wt p2 sin wt displaystyle frac v text L left t right i text L left t right frac omega I p L cos omega t I p sin left omega t right frac omega L sin left omega t frac pi 2 right sin omega t Bu AA AC gerilim genliginin AA akim genligine oraninin wL displaystyle scriptstyle omega L gibi bir bobin oldugunu gosteriyor ve AA gerilimini AA akimini 90 dereceyle takip eden bir bobin oldugunu soyluyor Bu sonuc kutupsal forma genellikle soyle kisaltilabilir Zbobin wLejp2 displaystyle Z text bobin omega Le j frac pi 2 Veya daha basit olarak Euler formulu kullanilarak Zbobin jwL displaystyle Z text bobin j omega L Resistans ve reaktansDirenc ve reaktans oz direncin genlik ve fazini birlikte su sekilde ifade ederler Z ZZ R2 X2 displaystyle Z sqrt ZZ sqrt R 2 X 2 8 arctan XR displaystyle theta arctan left frac X R right Bircok uygulamada gerilim ve akimin goreceli fazi cok da onemli olmadiginda sadece oz direncin genligi onemlidir Direnc Direnc R displaystyle scriptstyle R oz direncin gercel kismidir Tam rezistif empedansli bir aygitta akim ve gerilim arasinda faz farki yoktur R Z cos 8 displaystyle R Z cos theta quad Reaktans Reaktans X displaystyle scriptstyle X oz direncin sanal kismini ifade eder Sonlu reaktansa sahip bir bilesenin akimi ile gerilimi arasinda 8 displaystyle scriptstyle theta kadar bir faz farki vardir X Z sin 8 displaystyle X Z sin theta quad Tam reaktif bileseninde sinuzoidal gerilim akimin tam ceyrek evre farkladir Bu bilesenin devredeki enerjiyi cektigi ve sonra tekrar devreye geri verdigi anlamina gelir Saf reaktans hicbir guc harcamaz Kapasitif reaktans Kondansator tam reaktif empedansa sahiptir o da sinyal frekansi ile ters orantilidir Kondansator bir yalitkanla dielektrik olarak da bilinir ayrilan iki iletkenden olusur Dusuk frekanslarda kondansator ve yalitkandan akan yuk yoktur Induktif reaktans Induktif reaktans XL displaystyle scriptstyle X L sinyal frekansli f displaystyle scriptstyle f ve induktans L displaystyle scriptstyle L ile orantilidir XL wL 2pfL displaystyle X L omega L 2 pi fL quad Bobin iletken sargilardan olusur Elektromanyetik indukleme Faraday yasasina gore B displaystyle scriptstyle B manyetik alaninin yuk miktarindan dolayi bir akim cevriminde E displaystyle scriptstyle mathcal E emk sini geri verir akima karsi gerilim E dFBdt displaystyle mathcal E d Phi B over dt quad N displaystyle N sarimli bir bobindeki emk E NdFBdt displaystyle mathcal E N d Phi B over dt quad Geri emk akan akimin karsisindaki kaynaktir Sabit dogru akimda sifir yuk vardir ve bobin kisa devre gibi gozukur Alternatif akim ortalama bir zamanda yuke sahiptir ve frekansla orantilidir Bundan dolayidir ki induktif reaktans frekansla artar Ayrica bakinizEmpedans kontroluKaynakca Science p 18 1888 Oliver Heaviside Elektrikci p 212 23 Temmuz 1886 da Elektriksel sayfalara yazildi p64 AMS Bookstore ISBN 0 8218 3465 7 Kennelly Arthur Oz direnc IEEE 1893 AC Ohm s law 19 Subat 2011 tarihinde Wayback Machine sitesinde Hyperphysics Horowitz Paul 1989 1 The Art of Electronics Cambridge University Press ss 32 33 ISBN 0 521 37095 7 Capacitor inductor phase relationships 3 Agustos 2008 tarihinde Wayback Machine sitesinde Yokogawa Complex impedance 19 Temmuz 2010 tarihinde Wayback Machine sitesinde Hyperphysics Horowitz Paul 1989 1 The Art of Electronics Cambridge University Press ss 31 32 ISBN 0 521 37095 7
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State