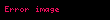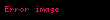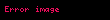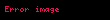Elektromanyetik sınır koşulları, elektromanyetik alanların iki malzeme arasındaki yüzeydeki ilişkilerini belirler. Yalıtkanlık sabiti ve/veya geçirgenlik sabitinin değiştiği arayüzlerde elektrik alan, elektrik akı yoğunluğu, manyetik alan ve manyetik akı yoğunluğunun değişimi ya da sürekliliği için farklı kurallar bulunmaktadır. Bu kurallar Maxwell denklemleri'nin integral gösterimleri ile türetilebilir.
Bu yüzey sınır koşulları, elektromanyetik sınır değer problemlerindeki Dirichlet ve Neumann tarzı sınır koşulları ile karıştırılmamalıdır.
Elektrik alan sınır koşulları

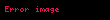 alanı için sınır koşulu Maxwell-Faraday yasası ile bulunur: w uzunluğunun 0'a limiti alınır.
alanı için sınır koşulu Maxwell-Faraday yasası ile bulunur: w uzunluğunun 0'a limiti alınır.Elektrik alan
Elektrik alan için sınır koşulu,
şeklinde tanımlanabilir. 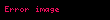
Elektrik akı yoğunluğu

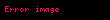 alanı için sınır koşulları Gauss yasası ile türetilebilir.
alanı için sınır koşulları Gauss yasası ile türetilebilir.Elektrik akı yoğunluğu lineer ortamlarda yalıtkanlık sabiti ile 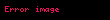
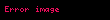
Şeklinde ifade edilir. Burada 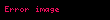
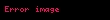
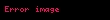
Manyetik alan sınır koşulları
Manyetik alan
Manyetik alan için sınır koşulu,
şeklinde gösterilir. Bu denklemde 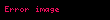
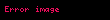
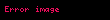
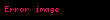
Yüksek frekanslarda yüzey katmanı etkisi nedeniyle iletkenlerde akım yüzeye yakın dar bir katmanda ilerler. Yüksek frekans devrelerinde bu akım yüzey akım yoğunluğu olarak modellenebilir.
Manyetik akı yoğunluğu

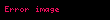 alanı için sınır koşullarının türetilmesi
alanı için sınır koşullarının türetilmesiManyetik akı yoğumluğu için sınır koşulu,
şeklinde verilebilir. Bu denklemde 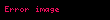
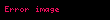

ile gösterilebilir.
Kaynakça
- ^ a b c d Kinayman & Aksun 2005, s. 19-22.
- ^ a b Cheng 2015, s. 111-113.
- ^ a b Cheng 2015, s. 199-200.
Kitaplar
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Elektromanyetik sinir kosullari elektromanyetik alanlarin iki malzeme arasindaki yuzeydeki iliskilerini belirler Yalitkanlik sabiti ve veya gecirgenlik sabitinin degistigi arayuzlerde elektrik alan elektrik aki yogunlugu manyetik alan ve manyetik aki yogunlugunun degisimi ya da surekliligi icin farkli kurallar bulunmaktadir Bu kurallar Maxwell denklemleri nin integral gosterimleri ile turetilebilir Bu yuzey sinir kosullari elektromanyetik sinir deger problemlerindeki Dirichlet ve Neumann tarzi sinir kosullari ile karistirilmamalidir Elektrik alan sinir kosullariE displaystyle mathbf E alani icin sinir kosulu Maxwell Faraday yasasi ile bulunur w uzunlugunun 0 a limiti alinir Elektrik alan Elektrik alan icin sinir kosulu n21 E1 E2 0 displaystyle mathbf n 21 times mathbf E 1 mathbf E 2 mathbf 0 seklinde tanimlanabilir n21 displaystyle mathbf n 21 2 ortamdan 1 ortama giden normal vektordur Bu kosul elektrik alanin teget bileseninin yuzey boyunca surekli oldugunu ifade eder E1t E2t displaystyle mathbf E 1t mathbf E 2t Elektrik aki yogunlugu D displaystyle mathbf D alani icin sinir kosullari Gauss yasasi ile turetilebilir Elektrik aki yogunlugu lineer ortamlarda yalitkanlik sabiti ile D1 e1E1 displaystyle mathbf D 1 varepsilon 1 mathbf E 1 ve D2 e2E2 displaystyle mathbf D 2 varepsilon 2 mathbf E 2 seklinde ifade edilebilir Elektrik aki yogunlugu icin sinir kosulu D1 D2 n21 ss displaystyle mathbf D 1 mathbf D 2 cdot mathbf n 21 sigma s Seklinde ifade edilir Burada n21 displaystyle mathbf n 21 2 ortamdan 1 ortama giden normal vektor ve ss displaystyle sigma s ise serbest yuzey yuk yogunlugudur Bu kosul elektrik aki yogunlugunun sinirda sureksiz oldugu ifade eder bu sureksizlik yuzey yuk yogumluguna esittir Yuzeyde serbest yuk olmamasi durumunda ss displaystyle sigma s o olarak alinir ve normal aki yogunluklari birbirine esitlenebilir Bu ozel durumda elektrik aki yogunlugu ve yalitkanlik sabiti arasindaki iliskiden faydalanilarak normal elektrik alan bilesenleri ile ilgili asagidaki ifade yazilabilir e1E1n e2E2n displaystyle varepsilon 1 mathbf E 1n varepsilon 2 mathbf E 2n Manyetik alan sinir kosullariManyetik alan Manyetik alan icin sinir kosulu n21 H1 H2 Js displaystyle mathbf n 21 times mathbf H 1 mathbf H 2 mathbf J s seklinde gosterilir Bu denklemde n21 displaystyle mathbf n 21 2 ortamdan 1 ortama giden normal vektoru Js displaystyle mathbf J s ise serbest yuzey akim yogunlugunu belirtir Her iki ortamin iletkenliginin sonlu olmasi durumunda serbest yuzey akimi tanimlanmaz Mukemmel iletken veya superiletken olmayan neredeyse tum fiziksel ortamlar icin Js displaystyle mathbf J s sifira esittir ve bunun sonucunda H displaystyle mathbf H in teget birleseninin surekli oldugu kabul edilebilir H1t H2t displaystyle mathbf H 1t mathbf H 2t Yuksek frekanslarda yuzey katmani etkisi nedeniyle iletkenlerde akim yuzeye yakin dar bir katmanda ilerler Yuksek frekans devrelerinde bu akim yuzey akim yogunlugu olarak modellenebilir Manyetik aki yogunlugu B displaystyle mathbf B alani icin sinir kosullarinin turetilmesi Manyetik aki yogumlugu icin sinir kosulu B1 B2 n21 0 displaystyle mathbf B 1 mathbf B 2 cdot mathbf n 21 0 seklinde verilebilir Bu denklemde n21 displaystyle mathbf n 21 2 ortamdan 1 ortama giden normal vektoru gosterir Bu kosul B displaystyle mathbf B akiminin yuzey boyunca surekli oldugunu gosterir Buna karsin manyetik alan ile manyetik aki yogunlugu arasindaki iliski lineer ortamlar icin B1 m1H1 displaystyle mathbf B 1 mu 1 mathbf H 1 ve B2 m2H2 displaystyle mathbf B 2 mu 2 mathbf H 2 ile tanimlanabilir Bundan yola cikarak manyetik alanin normal bilesenleri arasindaki iliski m1H1n m2H2n displaystyle mu 1 mathbf H 1n mu 2 mathbf H 2n ile gosterilebilir Kaynakca a b c d Kinayman amp Aksun 2005 s 19 22 a b Cheng 2015 s 111 113 a b Cheng 2015 s 199 200 KitaplarCheng David K 2015 Koksal Adnan Saka Birsen Ed Fundamentals of Engineering Electromagnetics Muhendislik Elektromanyetiginin Temelleri 2 bas Palme ISBN 978 975 8982 99 8 Kinayman Noyan Aksun M Irsadi 2005 Modern Microwave Circuits Ingilizce Norwood Artech House ISBN 9781844073832
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State