Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
Dalga vektörü, fizikte dalgayı ifade etmemize yardımcı olan vektördür. Herhangi bir vektör gibi, yöne ve büyüklüğe sahiptir. Büyüklüğü dalga sayısı ve açısal dalga sayısıdır (dalga boyu ile ters orantılıdır). Yönü ise genellikle dalga yayılımının yönüdür. İzafiyet kuramında, dalga vektörü, aynı zamanda olarak tanımlanabilir.
Tanımları
Ne yazık ki dalga vektörünün, kendi büyüklüklerinde 2π faktörü ile ayrılan iki genel tanımı vardır. Bir tanımı fizik ve ilgili alanlarda tercih edilirken, diğeri ise kristal bilimi ve ilgili alanlarda tercih edilir. Bunlara “fizik tanımı” ve “kristal bilimi tanımı” denir.
Fizik Tanımı
Mükemmel bir tek-boyutlu hareketli dalga denklemi aşağıdaki gibidir:
•x: yer •t: zaman •



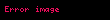
Kristal Bilimi Tanımı
Kristal biliminde, aynı dalgalar biraz farklı denklemler kullanılarak açıklanmıştır. Sırasıyla bir ve üç boyutlu dalgalar:
Farklılıklar: •Açısal frekans yerine, frekans kullanılmıştır (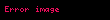
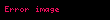

Dalga Vektörünün Yönü
Dalga vektörü noktaları "dalga yayılması yönünde" ayırt edilmelidir. "Dalga yayılımının yönü" bir dalganın enerji akışının ve küçük bir dalga paketinin hareket edeceği yöndür. Işık dalgaları için, ayrıca yönüdür. Dalga vektörü noktaları faz hızı yönündedir. Sabit fazın yüzeyinde, normal yönde, dalga vektörü noktaları, aynı zamanda dalganın önü olarak adlandırılır. Hava, herhangi bir gaz, sıvı ya da bazı katılar gibi kayıpsız eş yönlü bir ortam içinde, dalga vektörünün yönü dalga yayılma yönü ile tam olarak aynıdır. Homojen bir dalganın yüzeyinin büyüklüğü sabittir ve sabit bir faza sahiptir. Homojen olmayan dalgalar için bunlar söylenemez. Ancak, simetrik olmayan kristaldeki ışık dalgası ya da tortul kayadaki ses dalgası gibi eş yönlü olmayan ortamlarda dalga vektörü dalga yönüyle aynı olabilir.
Katı Hal Fiziğinde
Katı hal fiziğinde, kristalin içindeki bir elektronun “dalga vektörü” onun kuantum mekanik dalga fonksiyonudur. Bu elektron dalgaları sıradan sinüs dalgaları değildir, dalga vektörü bu kaplama dalga ile tanımlanır. Genellikle “fizik tanımı” kullanılır.
Özel Görelilikte
Tek renkli bir dalga ışını 4-vektör dalgası ile karakterize edilebilir.
Daha da açık yazmak gerekirse,
and
4-vektör dalgası, frekans ve 4-vektör dalgasının uzaysal bölümünün büyüklüğü arasında bir bağlantı verir:
4-vektör dalgası, dört ivme ile ilgidir.
Lorentz Dönüşümü
Dalga vektörünün Lorentz dönüşümü Doppler etksini elde etmek için tek yoldur. Lorentz matrisi:
Bir kaynak tarafından hızlı bir şekilde hareket eden ışık kaynağını, dünya çerçevesinde inceleyerek frekansını bulmak amacıyla, aşağıdaki gibi Lorentz dönüşümü uygulanır.
İçinde sadece 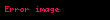
Not:
,
ile
arasındaki açının kosinüsüdür. Yani:
Uzaklaşan Kaynak
Örnekte olduğu gibi kaynaktan uzaklaşan bir gözlemci için:
Kaynağa Doğru Hareket
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Aralik 2014 Dalga vektoru fizikte dalgayi ifade etmemize yardimci olan vektordur Herhangi bir vektor gibi yone ve buyukluge sahiptir Buyuklugu dalga sayisi ve acisal dalga sayisidir dalga boyu ile ters orantilidir Yonu ise genellikle dalga yayiliminin yonudur Izafiyet kuraminda dalga vektoru ayni zamanda olarak tanimlanabilir TanimlariNe yazik ki dalga vektorunun kendi buyukluklerinde 2p faktoru ile ayrilan iki genel tanimi vardir Bir tanimi fizik ve ilgili alanlarda tercih edilirken digeri ise kristal bilimi ve ilgili alanlarda tercih edilir Bunlara fizik tanimi ve kristal bilimi tanimi denir Fizik Tanimi Mukemmel bir tek boyutlu hareketli dalga denklemi asagidaki gibidir ps x t Acos kx wt f displaystyle psi x t A cos kx omega t varphi x yer t zaman ps displaystyle psi dalganin bozulmasi A dalganin genligi f displaystyle varphi faz dengesi w displaystyle omega dalganin acisal frekansi k displaystyle k dalga sayisi Bu dalga x yonunde w k displaystyle omega k hiziyla hareket etmektedir Kristal Bilimi Tanimi Kristal biliminde ayni dalgalar biraz farkli denklemler kullanilarak aciklanmistir Sirasiyla bir ve uc boyutlu dalgalar ps x t Acos 2p kx nt f displaystyle psi x t A cos 2 pi kx nu t varphi ps r t Acos 2p k r nt f displaystyle psi left mathbf r t right A cos left 2 pi mathbf k cdot mathbf r nu t varphi right Farkliliklar Acisal frekans yerine frekans kullanilmistir 2pn w displaystyle 2 pi nu omega Bu esitlik Bu denklem icin onemli degil ama kristal biliminde yaygin bir uygulamadir Dalga sayisi k ve vektor olan k farkli sekillerde tanimlanmistir Burada k k 1 l displaystyle k mathbf k 1 lambda iken fizik taniminda k k 2p l displaystyle k mathbf k 2 pi lambda budur Dalga Vektorunun YonuDalga vektoru noktalari dalga yayilmasi yonunde ayirt edilmelidir Dalga yayiliminin yonu bir dalganin enerji akisinin ve kucuk bir dalga paketinin hareket edecegi yondur Isik dalgalari icin ayrica yonudur Dalga vektoru noktalari faz hizi yonundedir Sabit fazin yuzeyinde normal yonde dalga vektoru noktalari ayni zamanda dalganin onu olarak adlandirilir Hava herhangi bir gaz sivi ya da bazi katilar gibi kayipsiz es yonlu bir ortam icinde dalga vektorunun yonu dalga yayilma yonu ile tam olarak aynidir Homojen bir dalganin yuzeyinin buyuklugu sabittir ve sabit bir faza sahiptir Homojen olmayan dalgalar icin bunlar soylenemez Ancak simetrik olmayan kristaldeki isik dalgasi ya da tortul kayadaki ses dalgasi gibi es yonlu olmayan ortamlarda dalga vektoru dalga yonuyle ayni olabilir Kati Hal FizigindeKati hal fiziginde kristalin icindeki bir elektronun dalga vektoru onun kuantum mekanik dalga fonksiyonudur Bu elektron dalgalari siradan sinus dalgalari degildir dalga vektoru bu kaplama dalga ile tanimlanir Genellikle fizik tanimi kullanilir Ozel GorelilikteTek renkli bir dalga isini 4 vektor dalgasi ile karakterize edilebilir km wc k displaystyle k mu left frac omega c vec k right dd Daha da acik yazmak gerekirse km wc kx ky kz displaystyle k mu left frac omega c k x k y k z right and km wc kx ky kz displaystyle k mu left frac omega c k x k y k z right dd 4 vektor dalgasi frekans ve 4 vektor dalgasinin uzaysal bolumunun buyuklugu arasinda bir baglanti verir kmkm wc 2 kx2 ky2 kz2 0 displaystyle k mu k mu left frac omega c right 2 k x 2 k y 2 k z 2 0 dd 4 vektor dalgasi dort ivme ile ilgidir pm E c px py pz ℏw c ℏkx ℏky ℏkz ℏkm displaystyle p mu E c p x p y p z hbar omega c hbar k x hbar k y hbar k z hbar k mu dd Lorentz Donusumu Dalga vektorunun Lorentz donusumu Doppler etksini elde etmek icin tek yoldur Lorentz matrisi L g bg00 bgg0000100001 displaystyle Lambda begin pmatrix gamma amp beta gamma amp 0 amp 0 beta gamma amp gamma amp 0 amp 0 0 amp 0 amp 1 amp 0 0 amp 0 amp 0 amp 1 end pmatrix dd Bir kaynak tarafindan hizli bir sekilde hareket eden isik kaynagini dunya cercevesinde inceleyerek frekansini bulmak amaciyla asagidaki gibi Lorentz donusumu uygulanir ksm Lnmkobsn displaystyle k s mu Lambda nu mu k mathrm obs nu dd Icinde sadece m 0 displaystyle mu 0 bulunan sonuclara bakarsak ks0 L00kobs0 L10kobs1 L20kobs2 L30kobs3 displaystyle k s 0 Lambda 0 0 k mathrm obs 0 Lambda 1 0 k mathrm obs 1 Lambda 2 0 k mathrm obs 2 Lambda 3 0 k mathrm obs 3 dd wsc displaystyle frac omega s c gwobsc bgkobs1 displaystyle gamma frac omega mathrm obs c beta gamma k mathrm obs 1 gwobsc bgwobsccos 8 displaystyle quad gamma frac omega mathrm obs c beta gamma frac omega mathrm obs c cos theta Not cos 8 displaystyle cos theta k1 displaystyle k 1 ile k0 displaystyle k 0 arasindaki acinin kosinusudur Yani wobsws 1g 1 bcos 8 displaystyle frac omega mathrm obs omega s frac 1 gamma 1 beta cos theta dd dd Uzaklasan Kaynak Ornekte oldugu gibi kaynaktan uzaklasan bir gozlemci icin wobsws 1g 1 b 1 b21 b 1 b 1 b 1 b 1 b1 b displaystyle frac omega mathrm obs omega s frac 1 gamma 1 beta frac sqrt 1 beta 2 1 beta frac sqrt 1 beta 1 beta 1 beta frac sqrt 1 beta sqrt 1 beta dd Kaynaga Dogru Hareket wobsws 1 b1 b displaystyle frac omega mathrm obs omega s frac sqrt 1 beta sqrt 1 beta dd
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State