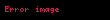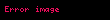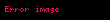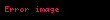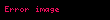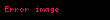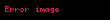Açısal frekans periyodik harekette birim zaman içinde kaç radyan olduğunun ölçüsüdür.
Radyan
Bir çemberin yarıçapı ile çevresi arasındaki ilişki
denklemiyle verilir.
Çember çevre uzunluğu
Çember yarıçap uzunluğu
Bir çemberde, yarıçap uzunluğundaki yay parçasını gören merkez açıya radyan denilir.Radyan rd kısaltmasıyla gösterilir. Periyodik harekette, çemberin bir periyodu birim zaman cinsinden T ise, her radyanın süresi (T / 2л) dir. Her periyotta 2 • л radyan olduğundan, saniyedeki radyan sayısı saniyedeki periyot sayısının 2 • л mislidir.
Radyan derece ilişkisi
Çember çevresi 360 derece veya 400 gradlık açıya sahiptir. Çevre aynı zamanda 2 • л adet radyana eşit olduğuna göre, radyan ile derece arasında sabit bir oran olmalıdır. Bir oranın derece cinsinden değeri,
(Noktadan sonra gelen basamaklarda ondalık kesir kullanılaıştır.Bu açının derece dakika saniye cinsinden karşılığı 57°17′45″dır.)
Frekans
Frekans periodik harekette birim zaman içindeki periyot sayısıdır. Şayet periyodik harekette her periodun süresi T ile veriliyorsa;
Açısal frekans ise, birim zamandaki radyan sayısıdır. (Gerçi derece veya grad da açı birimleridir. Ancak, açısal frekans denilince, aksi belirtilmedikçe, birim zaman içindeki radyan sayısı söz konusudur.) Açısal frekans ω simgesiyle gösterilir.
Denklemlerde açısal frekans şu şekilde gösterilir:
Örnek
Periyodu 1 mikrosaniye (1μs) olan bir periyodik hareketin frekansı;
Μikro öneki ve μ simgesi milyonda bir anlamına geldiğine göre μs bir saniyenin milyonda biri anlamına gelir.
Şayet bu hareket sinüzüdal bir hareket ise;
Fizikte açısal frekans
Fizikte açısal frekans çok yaygın olarak kullanılır.Benzer denklemlerle ifade edilen mekanikteki kütle-yay ve elektromanyetikteki kapasitans-indüktans problemlerinde açısal frekans şu şekilde yer alır:
- Yay kütle probleminde;
Burada,
yay sabiti
kütledir.
- İndütans kapasitans probleminde;
Burada da
indüktans
kapasitanstır.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Acisal frekans periyodik harekette birim zaman icinde kac radyan oldugunun olcusudur RadyanBir cemberin yaricapi ile cevresi arasindaki iliski C 2 p r displaystyle C 2 cdot pi cdot r denklemiyle verilir C displaystyle C Cember cevre uzunlugur displaystyle r Cember yaricap uzunlugup 3 141592 displaystyle pi approx 3 141592 Bir cemberde yaricap uzunlugundaki yay parcasini goren merkez aciya radyan denilir Radyan rd kisaltmasiyla gosterilir Periyodik harekette cemberin bir periyodu birim zaman cinsinden T ise her radyanin suresi T 2l dir Her periyotta 2 l radyan oldugundan saniyedeki radyan sayisi saniyedeki periyot sayisinin 2 l mislidir Radyan derece iliskisiCember cevresi 360 derece veya 400 gradlik aciya sahiptir Cevre ayni zamanda 2 l adet radyana esit olduguna gore radyan ile derece arasinda sabit bir oran olmalidir Bir oranin derece cinsinden degeri rd 180p 57 295780 displaystyle mbox rd frac 180 pi approx 57 295780 Noktadan sonra gelen basamaklarda ondalik kesir kullanilaistir Bu acinin derece dakika saniye cinsinden karsiligi 57 17 45 dir FrekansFrekans periodik harekette birim zaman icindeki periyot sayisidir Sayet periyodik harekette her periodun suresi T ile veriliyorsa f 1T displaystyle f frac 1 T Acisal frekans ise birim zamandaki radyan sayisidir Gerci derece veya grad da aci birimleridir Ancak acisal frekans denilince aksi belirtilmedikce birim zaman icindeki radyan sayisi soz konusudur Acisal frekans w simgesiyle gosterilir w 2 p f 2 pT displaystyle omega 2 cdot pi cdot f frac 2 cdot pi T Denklemlerde acisal frekans su sekilde gosterilir y t sin w t displaystyle y t sin omega cdot t OrnekPeriyodu 1 mikrosaniye 1ms olan bir periyodik hareketin frekansi Mikro oneki ve m simgesi milyonda bir anlamina geldigine gore ms bir saniyenin milyonda biri anlamina gelir T 1ms 1106 10 6 s displaystyle T 1 mu s frac 1 10 6 10 6 mbox s w 2 p10 6 2 p 106 rd s displaystyle omega frac 2 cdot pi 10 6 2 cdot pi cdot 10 6 mbox rd s Sayet bu hareket sinuzudal bir hareket ise y t sin 2 p 106 t displaystyle y t sin 2 cdot pi cdot 10 6 cdot t Fizikte acisal frekansFizikte acisal frekans cok yaygin olarak kullanilir Benzer denklemlerle ifade edilen mekanikteki kutle yay ve elektromanyetikteki kapasitans induktans problemlerinde acisal frekans su sekilde yer alir Yay kutle probleminde w km displaystyle omega sqrt frac k m Burada k displaystyle k yay sabitim displaystyle m kutledir Indutans kapasitans probleminde w 1LC displaystyle omega sqrt 1 over LC Burada da L displaystyle L induktansC displaystyle C kapasitanstir Ayrica bakinizPeriyodik Fonksiyon Trigonometri
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State