Cebirsel topoloji, topolojik uzayları cebirsel gereç ve yöntemlerle inceleyen matematik dalı. Matematikte bir kümenin üzerine döşenecek yapı, yönelinen matematik dalını belirler. Bir kümeye bir ya da birkaç işlem konarak sayılar kuramı ya da cebir yapmaya başlanabilir. Kümenin üzerine bir topoloji koyaraksa topoloji ve, ayrıca uzunluk koyarsak, geometri yapmaya başlanır. Üzerine topoloji konmuş bir uzayı (örneğin herhangi boyutlu bir Öklit uzayı) incelemek için kimi , aritmetik veya değişmezler tanımlanır; bunlar aracılığıyla topolojik uzayın özellikleri ayırdedilir. Örneğin tıkızlık, , sayılabilirlik bu tür değişmezlerdir. (birbirlerine homeomorfik) iki uzaydan biri bu değişmeze sahipse diğeri de buna sahip olmalıdır. Yani, eğer iki uzay için ayrı ayrı bakılan bir değişmez aynı değilse, bu iki uzay eşyapısal olmayacaktır. Yukarıda anılan en eski değişmezlerin hemen ardından inşa edilen klasik değişmezler cebirsel olanlardır.

İnşa
Topolojik uzaylara cebirsel değişmezler inşasında amaç şudur: her bir 







(1) 


(1') Ya da 

(2) 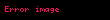

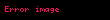

Topolojik uzaylara karşılık gelen ve bu koşulları sağlayan bir 









elde edilir. Birinci eşitlikten 


Şunu göstermiş olduk: (1) ve (2) sağlandığı sürece eşyapısal topolojik uzayların cebirsel nesneleri (grup, halka vs.) de birbirlerine eşyapısal olacak.
Örnekler
Burada birkaç cebirsel topolojik değişmez inşası özetlenecek.

Topolojik uzaylara karşılık gelen en basit cebirsel değişmezdir. Bir 


Öncelikle, 





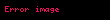







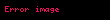






Örneğin gerçel sayı doğrusunun (



Yukarıdaki örneklerin aksine, 
Homoloji grupları
Homoloji grupları 





ifadesi 







Yukarıda tanımlanan 








Genel olarak, topolojik kategori üzerindeki homoloji teorisi, o topolojik kategori ile değişmeli bir kategori arasında bir izleç tir. 





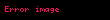

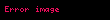
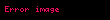
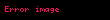


(1) Homotopy Koşulu: 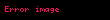

(2) Tamlık Koşulu: 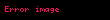

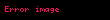

tamdır.
(3) Kesme Koşulu: 



(4) Boyut Koşulu: Sadece bir noktası olan uzayın bütün homoloji grupları 0 olmalıdır.
(5) Toplamsal Koşul: Uzayların topolojik toplamlarının homolojisi, homolojilerinin dik toplamı olmalıdır.
Bazı homoloji teorileri yukarıda verilen bütün koşulları sağlamayabilir. Tekil homoloji bu koşulların hepsini sağlar ve homoloji gruplarının hesaplanabilirliği bir sonucudur. Tekil homolojinin, kesme koşulunu sağladığı gösterilirken tekniği kullanılır.
Kohomoloji grupları
Homotopi grupları
Yukarıda anlatılan temel grup kısmında 
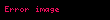

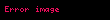














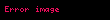
Bu cebirsel gruplar arasındaki en temel ilişki, lifli fonksiyonlara (fibrasyon) tayin edilen tam-uzun homotopi zinciridir. 


Bu tam-uzun zincirde kullanılan 













Cebirsel Topolojinin Temel Teoremleri
Bu kısımda 


Teorem : (Seifert-Van Kampen) 







Bu teoremin homoloji versiyonu Mayer-Vietoris teoremidir.
Teorem : (Mayer-Vietoris) 






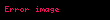

Homotopi ve homoloji grupları arasındaki münasepet Hurewicz teoremi olarak bilinmektedir:
Teorem : (Hurewicz Teoremi) 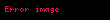




Bu teoremin en aşikar örneği, 

Kaynakça
- Hatcher, Allen (2002). Algebraic topology. Cambridge: Cambridge University Press.
- Munkres, James R. (2000). Topology (Second Edition). Prentice Hall. s. 537.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Cebirsel topoloji topolojik uzaylari cebirsel gerec ve yontemlerle inceleyen matematik dali Matematikte bir kumenin uzerine dosenecek yapi yonelinen matematik dalini belirler Bir kumeye bir ya da birkac islem konarak sayilar kurami ya da cebir yapmaya baslanabilir Kumenin uzerine bir topoloji koyaraksa topoloji ve ayrica uzunluk koyarsak geometri yapmaya baslanir Uzerine topoloji konmus bir uzayi ornegin herhangi boyutlu bir Oklit uzayi incelemek icin kimi aritmetik veya degismezler tanimlanir bunlar araciligiyla topolojik uzayin ozellikleri ayirdedilir Ornegin tikizlik sayilabilirlik bu tur degismezlerdir birbirlerine homeomorfik iki uzaydan biri bu degismeze sahipse digeri de buna sahip olmalidir Yani eger iki uzay icin ayri ayri bakilan bir degismez ayni degilse bu iki uzay esyapisal olmayacaktir Yukarida anilan en eski degismezlerin hemen ardindan insa edilen klasik degismezler cebirsel olanlardir Cebirsel topoloji 2 boyutlu kureInsaTopolojik uzaylara cebirsel degismezler insasinda amac sudur her bir X displaystyle X uzayi icin G X displaystyle G X olarak gosterilecek bir cebirsel nesne kurulacak Ayrica X displaystyle X uzayindan Y displaystyle Y uzayina surekli bir f displaystyle f gonderimi uzaylara karsilik gelen bu yeni cebirsel nesneler arasinda cebirsel yapilari gozeten ve f displaystyle f olarak gosterilecek gonderimler morfizmalar tarif edecek Yani topolojik kategoriden cebirsel kategorilere insa edilecek Ornegin G X displaystyle G X bir grup halka cisim olarak insa edilmisse f displaystyle f gonderimi grup halka cisim modul homomorfizmasi olacak Ustelik insa geregi bu cebirsel nesneler ve gonderimler su ozellikleri saglayacak 1 f X displaystyle f X displaystyle rightarrow Y displaystyle Y ve g X displaystyle g X displaystyle rightarrow Z displaystyle Z icin g f g f G X G Z displaystyle g circ f g circ f G X rightarrow G Z olacak 1 Ya da G displaystyle G nin cinsine gore g f f g G Z G X displaystyle g circ f f circ g G Z rightarrow G X olacak 2 brX X displaystyle br X X displaystyle rightarrow X displaystyle X birim gonderimine karsilik gelen brX G X displaystyle br X G X displaystyle rightarrow G X displaystyle G X birim gonderim olacak Topolojik uzaylara karsilik gelen ve bu kosullari saglayan bir G displaystyle G cebirsel nesnesi icat edilmis olsun Eger f displaystyle f X displaystyle X ten Y displaystyle Y ye bir topolojik esyapiysa f displaystyle f nin tersi vardir g displaystyle g diyelim ve g displaystyle g de bir esyapidir Dolayisiyla topolojik esyapinin tanimi geregi f g brY displaystyle f circ g br Y ve g f brX displaystyle g circ f br X olur Yukaridaki 1 ve 2 kosullarindan f g brY displaystyle f circ g br Y ve g f brX displaystyle g circ f br X elde edilir Birinci esitlikten f displaystyle f orten ikinciden f displaystyle f birebir olmak zorunda kalir Yani f displaystyle f bir cebirsel esyapi olur Sunu gostermis olduk 1 ve 2 saglandigi surece esyapisal topolojik uzaylarin cebirsel nesneleri grup halka vs de birbirlerine esyapisal olacak OrneklerBurada birkac cebirsel topolojik degismez insasi ozetlenecek Temel grup Egrilerde toplama islemi Topolojik uzaylara karsilik gelen en basit cebirsel degismezdir Bir X displaystyle X uzayi ve icinde bir x0 displaystyle x 0 noktasina karsilik p1 X x0 displaystyle pi 1 X x 0 olarak gosterilen bir gruptur Oncelikle X displaystyle X uzayinda surekli bir egri 0 1 kapali araligindan X displaystyle X e giden surekli bir gonderimdir a displaystyle a ve b displaystyle b iki egri olsun a displaystyle a ile b displaystyle b nin ucuca eklenmesiyle olusan egriyi a b displaystyle a cdot b olarak gosterelim x0 displaystyle x 0 noktasindan baslayan ve ayni noktada biten tum egrilerin kumesiniyse E displaystyle E ile gosterelim Eger herhangi iki egriyi anlatan gonderimler birbirlerine bu iki egriye denk egriler diyecegiz Gosterilebilir ki bu iliski E displaystyle E uzerinde gercekten bir denklik bagintisidir Boylece olusturulan denklik siniflarinin kumesi uzerinde ucuca ekleme islemi hala yani eger a displaystyle a egrisi c displaystyle c ye b displaystyle b egrisi de d displaystyle d ye homotopikse a b displaystyle a cdot b ile c d displaystyle c cdot d egrileri de birbirine homotopiktir Bu denklik siniflarini eleman olarak ve ucuca eklemeyi de islem olarak kabul eden cebirsel nesne gosterilebilir ki bir gruptur X displaystyle X ve x0 displaystyle x 0 verildiginde boylece insa edilen gruba X displaystyle X in x0 displaystyle x 0 daki temel grubu denir ve p1 X x0 displaystyle pi 1 X x 0 olarak gosterilir Ornegin gercel sayi dogrusunun R displaystyle R herhangi bir noktasindaki temel grubu tiriska asikar gruptur yani tek elemanli gruptur Oysa cemberin S1 displaystyle S 1 herhangi bir noktasindaki temel grubu Z displaystyle Z grubuna izomorfiktir Dolayisiyla R displaystyle R ile S1 displaystyle S 1 birbirlerine topolojik esyapisal olamazlar Bunu daha onceden de biliyorduk cunku R displaystyle R kompakt degildir ama S1 displaystyle S 1 kompakttir Yukaridaki orneklerin aksine p1 X x0 displaystyle pi 1 X x 0 genelde degismeli bir grup degildir Daha genel olarak verilen her grup icin temel grubu o grup olan bir uzay insa etmek mumkundur Homoloji gruplari Homoloji gruplari Hk X displaystyle H k X ile gosterilen gruplardir Temel grubun aksine homoloji gruplarinin insalari zor hesaplanabilirlikleri kolaydir Her X displaystyle X uzayina C X displaystyle C X ile gosterilen bir denk gelir Zincir kompleksi tanim geregi bir degismeli grup dizisinden ibarettir C X displaystyle C X in elemanlari Cj X displaystyle C j X ile gosterilir Bu zincir kompleksinin ardil koordinatlari displaystyle scriptstyle partial ile gosterilen sinir morfizmazlari ile baglanmistir Baska bir ifadeyle n 1Cn nCn 1 n 1 2C1 1C0 00 displaystyle dotsb overset scriptstyle partial n 1 longrightarrow C n overset scriptstyle partial n longrightarrow C n 1 overset scriptstyle partial n 1 longrightarrow dotsb overset scriptstyle partial 2 longrightarrow C 1 overset scriptstyle partial 1 longrightarrow C 0 overset scriptstyle partial 0 longrightarrow 0 ifadesi C X displaystyle C X i gostermektedir Bu displaystyle scriptstyle partial gonderimlerinin temel ozelligi 0 displaystyle scriptstyle partial scriptstyle partial 0 olmasidir Yani sinir morfimasi art arda iki kere uygulandiginda 0 morfizmasini verir Bu ozelligin bir sonucu olarak bir morfizmanin imaj kumesi bir sonraki mozfizmanin 0 kumesinin yani icindedir Imaj gruplarini Bk X displaystyle B k X ve cekirdekleri Zk X displaystyle Z k X ile gosterirsek Hk X displaystyle H k X grubu Zk X displaystyle Z k X in Bk X displaystyle B k X e bolumu ile bulunur Yukarida tanimlanan Hk X displaystyle H k X gruplari C X displaystyle C X gruplarinin fonksiyonlari olduklarindan C X displaystyle C X degistirildiginde farkli Hk X displaystyle H k X gruplari elde edilir C X displaystyle C X in insasina gore Hk X displaystyle H k X lere degisik isimler verilir C X displaystyle C X grubu X displaystyle X uzayinin tekil fonksiyonlari kullanilarak tanimlanmis ise elde edilen homoloji teorisine tekil homoloji teori denir Benzer sekilde basit homoloji demet homolojisi gibi farkli homoloji teoreleri elde etmek mumkundur Bu teorilerin bircogu CW displaystyle CW kategorisinde ayni sonucu verir Bazi ozel homoloji teorileri mesela Borel Moore homoloji teorisi lokal tikiz uzaylar icin dizayn edilmistir Genel olarak topolojik kategori uzerindeki homoloji teorisi o topolojik kategori ile degismeli bir kategori arasinda bir izlec tir T displaystyle T ile objeleri X A displaystyle X A olan ve oklari surekli gonderimler olan topolojik kategoriyi gosterelim H displaystyle H izleci her X A displaystyle X A ikilisine bir basamakli degismeli grup Hk X A displaystyle H k X A ve her surekli gonderim f X A displaystyle f X A displaystyle rightarrow Y B displaystyle Y B ye de bir morfizma f Hk X A displaystyle f H k X A displaystyle rightarrow Hk Y B displaystyle H k Y B atar Ayrica Hk X A displaystyle H k X A ile Hk A displaystyle H k A arasinda Hk X A displaystyle scriptstyle partial H k X A displaystyle rightarrow Hk 1 A displaystyle H k 1 A dogal gecis izlecleri vardir H displaystyle H nin bir homoloji teorisi olmasi icin asagida listelenen bes kosulun saglanmasi gerekir Bu kosul listesine Eilenberg Steenrod Milnor kosullari denir 1 Homotopy Kosulu f g X A displaystyle f g X A displaystyle rightarrow Y B displaystyle Y B haritalari homotopik iseler bunlara denk gelen morfizmalar ayni olmalidirlar 2 Tamlik Kosulu i A displaystyle iota colon A displaystyle rightarrow X displaystyle X ve j X displaystyle j colon X displaystyle rightarrow X A displaystyle X A dogal alt uzaylik haritalari ise Hk A iHk X j Hk X A Hk 1 A i displaystyle dotsb overset scriptstyle partial longrightarrow H k A overset iota longrightarrow H k X overset j longrightarrow H k X A overset scriptstyle partial longrightarrow H k 1 A overset iota longrightarrow dotsb tamdir 3 Kesme Kosulu U X displaystyle U subset X acik kumesinin kapanisi A displaystyle A nin icinde ise dahil olma haritasi k X U A U X A displaystyle k colon X U A U rightarrow X A ya denk gelen k H X U A U H X A displaystyle k colon H X U A U rightarrow H X A morfizma birerbir ve orten olmalidir 4 Boyut Kosulu Sadece bir noktasi olan uzayin butun homoloji gruplari 0 olmalidir 5 Toplamsal Kosul Uzaylarin topolojik toplamlarinin homolojisi homolojilerinin dik toplami olmalidir Bazi homoloji teorileri yukarida verilen butun kosullari saglamayabilir Tekil homoloji bu kosullarin hepsini saglar ve homoloji gruplarinin hesaplanabilirligi bir sonucudur Tekil homolojinin kesme kosulunu sagladigi gosterilirken teknigi kullanilir Kohomoloji gruplari Homotopi gruplari Yukarida anlatilan temel grup kisminda p1 X x displaystyle pi 1 X x tanimlandi Burada x X displaystyle x in X noktasi sabitlenmisti ve baslangic bitis noktalari x displaystyle x olan egrilerin homotopi siniflari kullanilmisti Baslangic ve bitis noktalari ayni olan egrilere dongu denir Bu egriler g S1 X displaystyle gamma colon scriptstyle mathbb S 1 rightarrow X tipinde surekli fonksiyonlardir Homotopi kavrami X displaystyle X in x displaystyle x teki dongulerinin surekli degisimini izah etmek icin dizayn edilmistir S1 displaystyle scriptstyle mathbb S 1 yerine cok boyutlu Sk displaystyle scriptstyle mathbb S k kurelerini kullanirsak dongu ler cok boyutlu donguler e donusurler Ornek olarak cember yani S1 displaystyle scriptstyle mathbb S 1 ve kure yani S2 displaystyle scriptstyle mathbb S 2 yi dusununuz Cemberin bir noktasindan baslayan donguler cemberin kendisidir veya tam katlaridir Kurenin bir noktasindan baslayan donguler cember seklindedirler fakat kure nin yuzeyi uzeyinde ki her noktadan bir kure daha yani cok boyutlu dongu baslamaktadir Benzer sekilde 3 boyutlu kure uzerindeki her nokta icin 1 boyutlu dongulerin 2 boyutlu kurelerin ve 3 boyutlu kurelerin homotopik degisimleri incelenebilir p1 X x displaystyle pi 1 X x grubu 1 boyutlu dongulerin surekli degisim homotopi siniflarinin grubu iken pk X x displaystyle pi k X x grubu k displaystyle k boyutlu kurelerin surekli degisim grubudur k sayisi biren buyuk ise pk X x displaystyle pi k X x degismelidir Ornek olarak p3 S2 Z displaystyle pi 3 scriptstyle mathbb S 2 scriptstyle mathbb Z pk 1 Sk Z2 displaystyle pi k 1 scriptstyle mathbb S k scriptstyle mathbb Z 2 pk 2 Sk Z2 displaystyle pi k 2 scriptstyle mathbb S k scriptstyle mathbb Z 2 ve k 5 displaystyle k geq 5 icin pk 3 Sk Z24 displaystyle pi k 3 scriptstyle mathbb S k scriptstyle mathbb Z 24 verilebilir Bu cebirsel gruplar arasindaki en temel iliski lifli fonksiyonlara fibrasyon tayin edilen tam uzun homotopi zinciridir p X B displaystyle p colon X rightarrow B lifi verilsin Doku kumesini F displaystyle F ile gosterelim Bu durumda homotopi gruplari arasinda soyle bir munasepet vardir pk F i pk X p pk B pk 1 F p1 X p1 B p0 F p0 X p0 B displaystyle dotsb overset longrightarrow pi k F overset iota sharp longrightarrow pi k X overset p sharp longrightarrow pi k B overset scriptstyle partial sharp longrightarrow pi k 1 F overset longrightarrow dotsb dotsb overset longrightarrow pi 1 X overset longrightarrow pi 1 B overset longrightarrow pi 0 F overset longrightarrow pi 0 X overset longrightarrow pi 0 B Fibrasyon Ornegi Bu tam uzun zincirde kullanilan p displaystyle p sharp morfizmasi p X B displaystyle p colon X rightarrow B tarafindan belirlenir i displaystyle iota sharp morfizmasi F displaystyle F doku kumesini X displaystyle X uzayina gomen i F X displaystyle iota colon F subset X tarafindan belirlenir displaystyle scriptstyle partial sharp ise baglanti morfizmasidir k 1 displaystyle k geq 1 icin pk X displaystyle pi k X bir gruptur fakat p0 X displaystyle pi 0 X bir grup degildir Bundan dolayi yukarida verilen zincirin 0 inci basamagindaki tam ligi sadece tanim ve deger kumelerinin ortusmesine denk gelir Yandaki sekilde bir fibrasyon ornegi izah edilmistir Resimde X displaystyle X uzayi E displaystyle E olarak alinmistir F displaystyle F uzayi dortgensel uzayin yani E displaystyle E nin icine cizilmis siyah bolgedir Cebirsel Topolojinin Temel TeoremleriBu kisimda X x0 displaystyle X x 0 ikilisinin verildigini kabul ediyoruz p1 X x0 displaystyle pi 1 X x 0 i hesaplamak icin kullanilan en temel teorem Seifert Van Kampen teoremidir Bu teoremin kullanilabilmesi icin X displaystyle X uzayinin kesisimleri bos olmayan iki acik kumenin birlesimi seklinde yazilabiliyor olmasi gerekmektedir Ayrica bu altuzaylarin ve kesisimlerinin temel gruplarinin bilinmesi gereklidir Teorem Seifert Van Kampen X U V displaystyle X U cup V x0 U V displaystyle x 0 in U cap V ve U V displaystyle U V kumeleri X displaystyle X icerisinde acik olsunlar Ayrica U V displaystyle U V ve U V displaystyle U cup V kumeleri yol baglantili olsunlar Bu durumda p1 U x0 p1 U V p1 V x0 displaystyle pi 1 U x 0 star pi 1 U cap V pi 1 V x 0 grubuyla p1 X x0 displaystyle pi 1 X x 0 grubu izomorfturlar Bu teoremin homoloji versiyonu Mayer Vietoris teoremidir Teorem Mayer Vietoris X displaystyle X uzayi U V displaystyle U V gibi iki altuzayin iclerinin birlesimi olsun iU U V U displaystyle iota U colon U cap V rightarrow U iV U V V displaystyle iota V colon U cap V rightarrow V ve jV U V displaystyle j V rightarrow U cup V gommeleri 0 0Ck U V iU iVCk U Ck V jU jVCk U V 00 displaystyle 0 overset 0 longrightarrow C k U cap V overset iota U iota V longrightarrow C k U C k V overset j U j V longrightarrow C k U cup V overset 0 longrightarrow 0 tam zincirini uretir Bu tam zincir ise asagidaki tam uzun homoloji zincirini uretir Hk U V iU iV Hk U Hk V jU jV Hk U V Hk 1 U V displaystyle dotsb overset longrightarrow H k U cap V overset iota U iota V ast longrightarrow H k U H k V overset j U j V ast longrightarrow H k U cup V overset longrightarrow H k 1 U cap V overset longrightarrow dotsb U V displaystyle U V ve U V displaystyle U cap V uzaylarinin homoloji modulleri biliniyorsa Mayer Vietoris zincirinin tamlik ozelligi kullanilarak X displaystyle X uzayinin homoloji modulleri elde edilebilir Homotopi ve homoloji gruplari arasindaki munasepet Hurewicz teoremi olarak bilinmektedir Teorem Hurewicz Teoremi x0 X displaystyle x 0 in X olsun p1 X x0 displaystyle pi 1 X x 0 ile H1 X displaystyle H 1 X esyapilidirlar Bu izomorfizm p1 X x0 displaystyle pi 1 X x 0 ile p1 X x0 p1 X x0 p1 X x0 displaystyle pi 1 X x 0 pi 1 X x 0 pi 1 X x 0 dogal izomorfizma ile aynidir Bu teoremin en asikar ornegi p1 X x0 displaystyle pi 1 X x 0 degismeli oldugunda p1 X x0 H1 X displaystyle pi 1 X x 0 H 1 X olmasidir KaynakcaHatcher Allen 2002 Algebraic topology Cambridge Cambridge University Press Munkres James R 2000 Topology Second Edition Prentice Hall s 537
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State














