Matematiğin bir alt dalı olan fonksiyonel analizde, tam normlu vektör uzayılarına Banach uzayı denir. Tanımı gereği, Banach uzayı, vektör uzunluğunun ve vektörler arasındaki mesafenin hesaplanmasına vesile olan bir metriğe sahip bir vektör uzayıdır ve bu metrik uzayda herhangi bir Cauchy vektör dizisinin her zaman uzayın içinde kalan ve iyi tanımlanmış bir limiti olması anlamında tamdır.
Banach uzayları, bu kavramı 1920-1922'de ve ile birlikte sistematik olarak inceleyen Polonyalı matematikçi Stefan Banach'ın adını taşır., Banach uzayı terimini ilk kullanan matematikçiydi. Banach uzayları, yirminci yüzyılın başlarında Hilbert, ve tarafından fonksiyon uzayları üzerine yapılan çalışmalardan ortaya çıktı .
Banach uzayları, fonksiyonel analizde merkezi bir rol oynar. Diğer analiz alanlarında incelenen uzaylar genellikle Banach uzaylarıdır.
Tanım
Tam olan bir Banach uzayı adı verilir.
Normlu uzay 

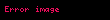



Norm tarafından üretilen metrik









- " Her gerçel
için bir
sayısı vardır öyle ki
"
özelliğini sağlarsa, bu diziye Cauchy dizisi adı verilir.
Norm tarafından üretilen metriğin tamlığı
Bir metrik uzayının 










Sonuç olarak, 


Örnekler
Aşağıdaki uzayların hepsi fonksiyonel analizin içinde çalışılan birer Banach uzayıdır.
gerçel sayılar cismi
ya da karmaşık sayılar
cismi olmak üzere Öklid uzayı
,
- Daha genel olarak
ya da karmaşık sayılar
cismi üzerinde tanımlı herhangi bir sonlu-boyutlu vektör uzayı
- Bir Banach uzayının herhangi kapalı bir altuzayı yine Banach uzayıdır. Mesela,
bir topolojik uzaysa ve
Banach uzayıysa,
'ten
'ye tanımlanan ve hem sürekli hem de sınırlı olan fonksiyonlar uzayı
yine Banachtır. Sonuç olarak, tıkız bir
uzayı için,
üzerinde tanımlı sürekli fonksiyonlar uzayı
de Banach uzayıdır. Aslında, vasıtasıyla, her Banach uzayı
'nin kapalı bir alt uzayına izomorftur.
- Hilbert uzayları
- Lebesgue uzayları:
,
,
,
, ,
- ,
,
- ,
uzayı,
uzayı,
- Tıkız Hausdorff uzayı üzerindeki sürekli fonksiyonlar uzayı C(K)
- uzayı
Ayrıca, matematiksel analizde uygulamaları olan ve yoğunlukla kullanılan şu uzaylar da Banach uzayıdır: , Bergman uzayı, , , , ,
Notlar
- ^ Tesadüf ki, Banach da buna karşılık daha sonraları terimini kullanmıştır.
- ^ Bu cisim genelde,
ya da
olur. Belirli bir cisim kastedilmiyorsa, Almanca terim Körper kaynaklı
kullanılır.
- ^ Burada belirli sözünden kastedilen şudur. Eğer
üzerinde
normu yerine başka bir norm
alınsaydı, o zaman
ile
aynı Banach uzayı olmazdı. Bu durum, normlar olsa bile değişmezdi. Yine de, bir vektör uzayı üzerinde tanımlı denk normlar bir denklik bağıntısı oluştururlar.
- ^ Normlu bir
uzayı üzerinde bir norm tarafından doğurulan bir
metriği adı verilen özelliği sağlar. Yani, her
için
vardır. Bu özellik, ancak ve ancak yine bütün
için
gerçeklenirse olur. Öbür taraftan, bir metrik uzayda sağlanması, bu metrik uzayın normlu bir uzay tarafından doğurulduğunu tek başına göstermez. Bunun olması için, yanı sıra bir de özelliği gerekir. Bu özellik, bir
fonksiyonu için
- Her
ve
için,
vardır.
- Her
- ^ Metriği veya normu vurgulamak için
'de Cauchy,
-Cauchy veya
-Cauchy tanımları da kullanılır.
Kaynakça
- ^ Bourbaki 1987, V.87
- ^ Narici & Beckenstein 2011, s. 93.
Referanslar
- Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Eggleston, H.G.; Madan, S. tarafından çevrilmiştir. Berlin New York: Springer-Verlag. .
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan fonksiyonel analizde tam normlu vektor uzayilarina Banach uzayi denir Tanimi geregi Banach uzayi vektor uzunlugunun ve vektorler arasindaki mesafenin hesaplanmasina vesile olan bir metrige sahip bir vektor uzayidir ve bu metrik uzayda herhangi bir Cauchy vektor dizisinin her zaman uzayin icinde kalan ve iyi tanimlanmis bir limiti olmasi anlaminda tamdir Banach uzaylari bu kavrami 1920 1922 de ve ile birlikte sistematik olarak inceleyen Polonyali matematikci Stefan Banach in adini tasir Banach uzayi terimini ilk kullanan matematikciydi Banach uzaylari yirminci yuzyilin baslarinda Hilbert ve tarafindan fonksiyon uzaylari uzerine yapilan calismalardan ortaya cikti Banach uzaylari fonksiyonel analizde merkezi bir rol oynar Diger analiz alanlarinda incelenen uzaylar genellikle Banach uzaylaridir TanimTam olan bir Banach uzayi adi verilir Normlu uzay X displaystyle X ile gosterilsin X displaystyle X uzerinde tanimli norm displaystyle cdot ise Banach uzayinin gosterimi X displaystyle X cdot olur Ancak sadece bir tane Banach uzayindan bahsediliyorsa veya norma vurgu yapmaya gerek yoksa X displaystyle X cdot yerine sadece X displaystyle X bir Banach uzayidir da denir Norm tarafindan uretilen metrik X displaystyle X cdot normlu uzayi skaler bir cisim K displaystyle mathbb K uzerinde tanimlanmis bir X displaystyle X vektor uzayindan ve belirli bir norm fonksiyonu olan X R displaystyle cdot X to mathbb R ile tanimlanir Butun normlar gibi bu norm da bir metrik uzayi dogurur Bu metrige denir Eger bu metrik d displaystyle d ile gosterilirse o zaman su sekilde tanimlanir d x y y x x y displaystyle d x y y x x y Bu tanim altinda norm ozelliklerinden faydalanarak d displaystyle d nin gercekten bir metrik oldugu gosterilebilir Sonuc olarak X displaystyle X bir metrik uzayi olur ve X d displaystyle X d ile gosterilir X d displaystyle X d icinde bir xj j 1 displaystyle x j j 1 infty dizisi Her gercel e gt 0 displaystyle varepsilon gt 0 icin bir N Z displaystyle N in mathbb Z sayisi vardir oyle kid xn xm xn xm lt e m n N displaystyle d left x n x m right left x n x m right lt varepsilon quad forall m n geq N dd ozelligini saglarsa bu diziye Cauchy dizisi adi verilir Norm tarafindan uretilen metrigin tamligi Bir metrik uzayinin X d displaystyle X d deki her xj j 1 displaystyle x j j 1 infty Cauchy dizisinin limiti yine X displaystyle X teyse o zaman d displaystyle d ye X d displaystyle X d ye ise tam metrik uzay denir Burada limit kavrami X d displaystyle X d baglaminda limn xn x displaystyle lim n to infty x n x olarak yazilabilir Ayni zamanda xn x d xn x displaystyle left x n x right d left x n x right olacagi icin dizinin x displaystyle x degerine yakinsamasi daha once verilen limit ifadesine denk olarak R displaystyle mathbb R baglaminda limn xn x 0 displaystyle lim n to infty left x n x right 0 olarak yazilabilir Sonuc olarak X d displaystyle X d tam metrik uzaysa X displaystyle X cdot Banach uzayidir X displaystyle X cdot normlu uzayi eger Banach uzayiysa o zaman displaystyle cdot norm fonksiyonuna tam norm denir OrneklerAsagidaki uzaylarin hepsi fonksiyonel analizin icinde calisilan birer Banach uzayidir F displaystyle mathbb F gercel sayilar cismi R displaystyle mathbb R ya da karmasik sayilar C displaystyle mathbb C cismi olmak uzere Oklid uzayi Fn displaystyle mathbb F n Daha genel olarak R displaystyle mathbb R ya da karmasik sayilar C displaystyle mathbb C cismi uzerinde tanimli herhangi bir sonlu boyutlu vektor uzayi Bir Banach uzayinin herhangi kapali bir altuzayi yine Banach uzayidir Mesela X displaystyle X bir topolojik uzaysa ve Y displaystyle Y Banach uzayiysa X displaystyle X ten Y displaystyle Y ye tanimlanan ve hem surekli hem de sinirli olan fonksiyonlar uzayi B X Y displaystyle B X Y yine Banachtir Sonuc olarak tikiz bir K displaystyle K uzayi icin K displaystyle K uzerinde tanimli surekli fonksiyonlar uzayi C K Y displaystyle C K Y de Banach uzayidir Aslinda vasitasiyla her Banach uzayi C K R displaystyle C K mathbb R nin kapali bir alt uzayina izomorftur Hilbert uzaylari Lebesgue uzaylari ℓpn displaystyle ell p n ℓ n displaystyle ell infty n ℓp displaystyle ell p ℓ1 displaystyle ell 1 Lp displaystyle L p c0 displaystyle c 0 bv0 displaystyle operatorname bv 0 uzayi bs displaystyle operatorname bs uzayi Tikiz Hausdorff uzayi uzerindeki surekli fonksiyonlar uzayi C K uzayi AC a b displaystyle operatorname AC a b Ayrica matematiksel analizde uygulamalari olan ve yogunlukla kullanilan su uzaylar da Banach uzayidir Bergman uzayi Notlar Tesaduf ki Banach da buna karsilik daha sonralari terimini kullanmistir Bu cisim genelde C displaystyle mathbb C ya da R displaystyle mathbb R olur Belirli bir cisim kastedilmiyorsa Almanca terim Korper kaynakli K displaystyle mathbb K kullanilir Burada belirli sozunden kastedilen sudur Eger X displaystyle X uzerinde displaystyle cdot normu yerine baska bir norm displaystyle cdot prime alinsaydi o zaman X displaystyle X cdot ile X displaystyle left X cdot prime right ayni Banach uzayi olmazdi Bu durum normlar olsa bile degismezdi Yine de bir vektor uzayi uzerinde tanimli denk normlar bir denklik bagintisi olustururlar Normlu bir X displaystyle X uzayi uzerinde bir norm tarafindan dogurulan bir d displaystyle d metrigi adi verilen ozelligi saglar Yani her x y z X displaystyle x y z in X icin d x y d x z y z displaystyle d x y d x z y z vardir Bu ozellik ancak ve ancak yine butun x y X displaystyle x y in X icin d x y d x y 0 displaystyle d x y d x y 0 gerceklenirse olur Obur taraftan bir metrik uzayda saglanmasi bu metrik uzayin normlu bir uzay tarafindan doguruldugunu tek basina gostermez Bunun olmasi icin yani sira bir de ozelligi gerekir Bu ozellik bir f X R displaystyle f X mapsto mathbb R fonksiyonu icin Her x X displaystyle x in X ve s K displaystyle s in mathbb K icin f sx s f x displaystyle f sx s f x vardir olarak tanimlanir Metrigi veya normu vurgulamak icin X d displaystyle X d de Cauchy d displaystyle d Cauchy veya displaystyle cdot Cauchy tanimlari da kullanilir Kaynakca Bourbaki 1987 V 87 Narici amp Beckenstein 2011 s 93 ReferanslarBourbaki Nicolas 1987 1981 Topological Vector Spaces Chapters 1 5 Elements de mathematique Eggleston H G Madan S tarafindan cevrilmistir Berlin New York Springer Verlag ISBN 3 540 13627 4 Narici Lawrence Beckenstein Edward 2011 Topological Vector Spaces Pure and applied mathematics Second ed Boca Raton FL CRC Press ISBN 978 1584888666
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State