Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
Geometride, afin dönüşüm (Latinceden, affinis, "birbirine bağlılık") veya ilgin dönüşüm, arasında noktaları, düz çizgileri ve düzlemleri koruyan bir eşlemedir. Ayrıca, paralel çizgi kümeleri bir afin dönüşüm sonrası paralel kalır. Bir afin dönüşümde aynı doğru üzerinde duran noktalar arasındaki mesafe oranları korunmasına rağmen, çizgiler arasındaki açılar ve noktalar arasındaki mesafeler korunmayabilir.

Öteleme, dönme, , , , yansıma, ve bunların kombinasyonları birer ilgin dönüşüm örneğidir.
ve için, her afin dönüşümü formundadır. Burada bir doğrusal dönüşümü, bir vektörü ( uzayında) ve bir vektörü ( uzayında) ifade eder. Doğrusal dönüşümün aksine, ilgin dönüşüm doğrusal bir uzayda sıfır noktasının korunmasını gerektirmez. Bu yüzden, her doğrusal dönüşüm ilgindir, ama her ilgin dönüşüm doğrusal değildir.
Öklid uzayı çok amaç için bir afin uzay olarak düşünülüyor olabilir,Afin uzayı kavramı daha genel olmasına rağmen (yani, tüm Öklid uzaylar afin, ama Öklidyen olmayan olan afin uzaylarda vardır).,kartezyen koordinatlar Öklid uzaylarinda yer alır, Bir afin haritanın her koordinatı ; o zaman, () herhangi bir afin dönüşüm bir doğrusal dönüşüme eşdeğerdir bir aşağıdadır.
Matematiksel Tanımı
İki arasında (bu,iki uzay noktaları arasındaki vektörler olup) vektörler üzerinde hareket noktalarının bir göndermesidir.
:
veya
.
Aşağıda başka birkaç yolla bu tanımı yorumlayabiliriz..



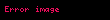
Eğer orijin 


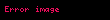
buraya gönderir
yani
tarafından aşağıda çevrilen sonuç olarak bu,sezgisel bir
bir öteleme ile doğrusal harita oluşur.
Alternatif tanımlar
Ayni alan üzerinde iki 




Bir diğer ifadeyle, 
Gösterimler
Yukarıda gösterilen, bir afin gönnderme iki fonksiyonun : bir öteleme ve bir . Olağan vektör cebri doğrusal göndermeler gönderimi için matris çarpımı ve ötelemeler gösterimi için kullanılıyor. Resmi olarak,sonlu-boyutlu durum içinde, eğer doğrusal gönderme bir matris A ile bir çarpım olarak ve bir vektör 

Genişletilmiş matris
Bir ve bir genişletilmiş vektör kullanılıyor, bunu hem öteleme ve hem doğrusal gönderme bir tek matris çarpımı ile temsil etmek mümkündür.Bu teknikle tüm vektörleri genişletmek gerekir sonda bir "1" ile genişler,ve tüm matrisler altta sıfırın bir fazladan satırı kadar genişletiliyor,bir fazladan sütun sağa-öteleme vektörü-ve sağ alt köşe içinde bir "1". Eğer A bir matris ise,
aşağıdakine eşdeğerdir.
Düzlemin afin dönüşümü

Iki gerçek boyutlu Afin dönüşümler dahil:
- Tam öteleme,
- Başka bir yönde bir çizgi ile ilgili olarak belirli bir yönde (dik olması gerekmez), öteleme ile birlikte ölçekleme yönünde saf değildir; genel bir anlamda "ölçeklendirme" alarak bu durumda ölçek faktörü içeren () sıfırdır veya negatiftir; sonra ise ve öteleme ile birlikte içerir,
- dönmeyle kombine ile bir öteleme,
- Bir benzerlik ve bir öteleme ile birlikte veya
- Bir benzeşim ve bir öteleme ile birlikte .
genel afin gösteriminin görselleştirilmesi için paralelkenarlar ABCD ve A′B′C′D olarak ′etiketlenir. Seçilen herhangi iki nokta burada,A dan A′ya T planında afin dönüşüm olarak alınıyor ve her tepe eşdeğerdir. Varsayalımki dejenere durumları dışlıyoruz burada ABCDsıfır bölge idi,ayrıca burada tek benzersiz afin dönüşüm T dir. ABCD tabanlı paralelkenarın bir bütün gridi dışarı sürülerek,herhangi bir T(A) belirtilerek P noktası tarafından belirlenen bu imaj T(P) dir. T(A) = A′,T AB çizgi parçasına uygulanan A′B′dir, T' çizgi parçasına uygulanan AC A′C′dir ve A tabanlı vektörlerin T sırasıyla skaler topluluğudur.[Eğer A, E, F eşdoğrusal ise kesir(AF)uzunluğu/(AE)uzunluğu eşittir.(A′F′)uzunluğu/(A′E′) uzunluğu.] geometrik T ye göre ABCD yi A′B′C′D′ tabanına grid dönüştürür .
Afin dönüşümlerin uzunlukları veya açılarını sırası yok etmek için bu alanı sabit bir katsayısı ile çarpmak gerekir.
- A′B′C′D′ bölgesi / ABCD bölgesi.
olarak verilen bir T ye doğrudan (sıralı yönlendirme ), veya dolaylı (ters yönlendirme) olabilir ve bu işaret olarak etkisi tarafından belirlenen bölgedir (örnek için vektörlerin çapraz çarpım'ı tanımlanır).
Afin dönüşümlerin örnekleri
Reel sayılar üzerinde Afin dönüşümler
f : R → R fonksiyonları, f(x) = mx + c ile m ve c sabiti,olağan afin dönüşümler yapar.
Sonlu bir alan üzerinde afin dönüşüm
Afin bir dönüşüm içeren (28) denklemi aşağıdaki ifade edilmiştir:
burada [M] ve {v} .
|
Örneğin, gösterimi içinde aşağıdaki hesaplanan elemanın afin dönüşümü büyük-sonlu gösterim içinde {CA} ={a} = y7 + y6 + y3 + y = {11001010} :
Böylece, {a′} = y7 + y6 + y5 + y3 + y2 + 1 = {11101101} = {ED} afin dönüşümü elde edilir.
Düzlem geometride Afin dönüşüm

ℝ2 içinde,dönüşüm tarafından verilen gönderme ile sağ tarafta gerçekleştirilen gösterim:
Orijinal üçgen (kırmızı) üç köşe noktaları dönüşüm ile yeni üçgen(mavi) oluşturan üç yeni nokta verir. Bu dönüşüm orijinal üçgeni eğriltir ve öteler. Aslında, her üçgen afin bir dönüşüm başka bir üçgen ile ilgilidir.Bu, aynı zamanda tüm paralelkenarlar için değil,tüm dörtgenler için de geçerlidir.
Ayrıca bakınız
Notlar
Bu maddedeki bilgilerin için ek kaynaklar gerekli. () |
Kaynakça
Dış bağlantılar
- . Hakan Haberdar, University of Houston. 11 Şubat 2015 tarihinde kaynağından arşivlendi.
- Hazewinkel, Michiel, (Ed.) (2001), "Affine transformation", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- Geometric Operations: Affine Transform 10 Ekim 2013 tarihinde Wayback Machine sitesinde ., R. Fisher, S. Perkins, A. Walker and E. Wolfart.
- Eric W. Weisstein, Affine Transformation (MathWorld)
- Affine Transform 12 Ekim 2013 tarihinde Wayback Machine sitesinde . by Bernard Vuilleumier, .
- Affine Transformation on PlanetMath 1 Mart 2012 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Subat 2017 Bu maddenin iceriginin Turkcelestirilmesi veya Turkce dilbilgisi ve kurallari dogrultusunda duzeltilmesi gerekmektedir Bu maddedeki yazim ve noktalama yanlislari ya da anlatim bozukluklari giderilmelidir Yabanci sozcukler yerine Turkce karsiliklarinin kullanilmasi karakter hatalarinin duzeltilmesi dilbilgisi hatalarinin duzeltilmesi vs Duzenleme yapildiktan sonra bu sablon kaldirilmalidir Geometride afin donusum Latinceden affinis birbirine baglilik veya ilgin donusum arasinda noktalari duz cizgileri ve duzlemleri koruyan bir eslemedir Ayrica paralel cizgi kumeleri bir afin donusum sonrasi paralel kalir Bir afin donusumde ayni dogru uzerinde duran noktalar arasindaki mesafe oranlari korunmasina ragmen cizgiler arasindaki acilar ve noktalar arasindaki mesafeler korunmayabilir bir egrelti benzerifraktal resmi afin gosterimdir Ve her egreltinin otunun yapraklaribir afin donusum tarafindan bir digeri ile iliskilidir Ornegin yansima donme genisleme ve cevirme kirmizi yaprak kombinasyonu tarafindan mavi yaprak haline donusturulebilir Oteleme donme yansima ve bunlarin kombinasyonlari birer ilgin donusum ornegidir X displaystyle X ve Y displaystyle Y icin her f X Y displaystyle f X to Y afin donusumu x Mx b displaystyle x mapsto Mx b formundadir Burada M displaystyle M bir dogrusal donusumu x displaystyle x bir vektoru X displaystyle X uzayinda ve b displaystyle b bir vektoru Y displaystyle Y uzayinda ifade eder Dogrusal donusumun aksine ilgin donusum dogrusal bir uzayda sifir noktasinin korunmasini gerektirmez Bu yuzden her dogrusal donusum ilgindir ama her ilgin donusum dogrusal degildir Oklid uzayi cok amac icin bir afin uzay olarak dusunuluyor olabilir Afin uzayi kavrami daha genel olmasina ragmen yani tum Oklid uzaylar afin ama Oklidyen olmayan olan afin uzaylarda vardir kartezyen koordinatlar Oklid uzaylarinda yer alir Bir afin haritanin her koordinati o zaman herhangi bir afin donusum bir dogrusal donusume esdegerdir bir asagidadir Matematiksel TanimiIki arasinda bu iki uzay noktalari arasindaki vektorler olup vektorler uzerinde hareket noktalarinin bir gondermesidir f A B displaystyle f mathcal A to mathcal B Semboller bu noktalarin herhangi bir cifti icin bir f lineer donusumu olan f yi belirler P Q A displaystyle P Q in mathcal A f P f Q f PQ displaystyle overrightarrow f P f Q varphi overrightarrow PQ veya f Q f P f Q P displaystyle f Q f P varphi Q P Asagida baska birkac yolla bu tanimi yorumlayabiliriz O A displaystyle O in mathcal A secersek imaji B displaystyle B olur f O B displaystyle f O in mathcal B bu demektir ki bir vektor x displaystyle vec x f O x B f x displaystyle f O vec x mapsto B varphi vec x Eger orijin O B displaystyle O in mathcal B secilirse bu bir afin donusum olarak ayristirilabilir ve B displaystyle B goruntusuf O B displaystyle f O in mathcal B ise herhangi bir x displaystyle vec x vektoru icin bunun anlami g O x O f x displaystyle g O vec x mapsto O varphi vec x g A B displaystyle g mathcal A to mathcal B buraya gonderir O O displaystyle O mapsto O yani b O B displaystyle vec b overrightarrow O B tarafindan asagida cevrilen sonuc olarak bu sezgisel bir f displaystyle f bir oteleme ile dogrusal harita olusur Alternatif tanimlar Ayni alan uzerinde iki A displaystyle mathcal A ve B displaystyle mathcal B veriliyor f A B displaystyle f mathcal A to mathcal B fonksiyonu afin bir gondermedir ancak ve ancak her aile icin ai li i I displaystyle a i lambda i i in I A displaystyle mathcal A agirlik noktalaridir boylece i Ili 1 displaystyle sum i in I lambda i 1 f i Iliai i Ilif ai displaystyle f left sum i in I lambda i a i right sum i in I lambda i f a i Bir diger ifadeyle f displaystyle f ler korunur GosterimlerYukarida gosterilen bir afin gonnderme iki fonksiyonun bir oteleme ve bir Olagan vektor cebri dogrusal gondermeler gonderimi icin matris carpimi ve otelemeler gosterimi icin kullaniliyor Resmi olarak sonlu boyutlu durum icinde eger dogrusal gonderme bir matris A ile bir carpim olarak ve bir vektor b displaystyle vec b nin toplami oteleme olarak gosteriliyorsa bir vektor x displaystyle vec x uzerinde hareketi bir afin gonderme f displaystyle f olarak gosterilebilir y f x Ax b displaystyle vec y f vec x A vec x vec b Genisletilmis matris source source source source source source 2D duzlem uzerinde afin donusumler uc boyutlu olarak gerceklestirilebilir oteleme z ekseni uzerinde boyunca kesme yapilir ve donme z ekseni etrafinda yapilir Bir ve bir genisletilmis vektor kullaniliyor bunu hem oteleme ve hem dogrusal gonderme bir tek matris carpimi ile temsil etmek mumkundur Bu teknikle tum vektorleri genisletmek gerekir sonda bir 1 ile genisler ve tum matrisler altta sifirin bir fazladan satiri kadar genisletiliyor bir fazladan sutun saga oteleme vektoru ve sag alt kose icinde bir 1 Eger A bir matris ise y 1 Ab 0 01 x 1 displaystyle begin bmatrix vec y 1 end bmatrix begin bmatrix A amp vec b 0 ldots 0 amp 1 end bmatrix begin bmatrix vec x 1 end bmatrix asagidakine esdegerdir y Ax b displaystyle vec y A vec x vec b Duzlemin afin donusumuMerkezi bir genlesme Ucgenler A1B1Z A1C1Z ve B1C1Z eslestirilir olsun sirasiyla A2B2Z A2C2Z ve B2C2Z Iki gercek boyutlu Afin donusumler dahil Tam oteleme Baska bir yonde bir cizgi ile ilgili olarak belirli bir yonde dik olmasi gerekmez oteleme ile birlikte olcekleme yonunde saf degildir genel bir anlamda olceklendirme alarak bu durumda olcek faktoru iceren sifirdir veya negatiftir sonra ise ve oteleme ile birlikte icerir donmeyle kombine ile bir oteleme Bir benzerlik ve bir oteleme ile birlikte veya Bir benzesim ve bir oteleme ile birlikte genel afin gosteriminin gorsellestirilmesi icin paralelkenarlar ABCD ve A B C D olarak etiketlenir Secilen herhangi iki nokta burada A dan A ya T planinda afin donusum olarak aliniyor ve her tepe esdegerdir Varsayalimki dejenere durumlari disliyoruz burada ABCDsifir bolge idi ayrica burada tek benzersiz afin donusum T dir ABCD tabanli paralelkenarin bir butun gridi disari surulerek herhangi bir T A belirtilerek P noktasi tarafindan belirlenen bu imaj T P dir T A A T AB cizgi parcasina uygulanan A B dir T cizgi parcasina uygulanan AC A C dir ve A tabanli vektorlerin T sirasiyla skaler toplulugudur Eger A E F esdogrusal ise kesir AF uzunlugu AE uzunlugu esittir A F uzunlugu A E uzunlugu geometrik T ye gore ABCD yi A B C D tabanina grid donusturur Afin donusumlerin uzunluklari veya acilarini sirasi yok etmek icin bu alani sabit bir katsayisi ile carpmak gerekir A B C D bolgesi ABCD bolgesi olarak verilen bir T ye dogrudan sirali yonlendirme veya dolayli ters yonlendirme olabilir ve bu isaret olarak etkisi tarafindan belirlenen bolgedir ornek icin vektorlerin capraz carpim i tanimlanir Afin donusumlerin ornekleriReel sayilar uzerinde Afin donusumler f R R fonksiyonlari f x mx c ile m ve c sabiti olagan afin donusumler yapar Sonlu bir alan uzerinde afin donusum Afin bir donusum iceren 28 denklemi asagidaki ifade edilmistir a M a v displaystyle a M a oplus v burada M ve v M a 1000111111000111111000111111000111111000011111000011111000011111 displaystyle M a begin bmatrix 1 amp 0 amp 0 amp 0 amp 1 amp 1 amp 1 amp 1 1 amp 1 amp 0 amp 0 amp 0 amp 1 amp 1 amp 1 1 amp 1 amp 1 amp 0 amp 0 amp 0 amp 1 amp 1 1 amp 1 amp 1 amp 1 amp 0 amp 0 amp 0 amp 1 1 amp 1 amp 1 amp 1 amp 1 amp 0 amp 0 amp 0 0 amp 1 amp 1 amp 1 amp 1 amp 1 amp 0 amp 0 0 amp 0 amp 1 amp 1 amp 1 amp 1 amp 1 amp 0 0 amp 0 amp 0 amp 1 amp 1 amp 1 amp 1 amp 1 end bmatrix v 11000110 displaystyle v begin bmatrix 1 1 0 0 0 1 1 0 end bmatrix Ornegin gosterimi icinde asagidaki hesaplanan elemanin afin donusumu buyuk sonlu gosterim icinde CA a y7 y6 y3 y 11001010 a0 a0 a4 a5 a6 a7 1 0 0 0 1 1 1 1 displaystyle a 0 a 0 oplus a 4 oplus a 5 oplus a 6 oplus a 7 oplus 1 0 oplus 0 oplus 0 oplus 1 oplus 1 oplus 1 1 a1 a0 a1 a5 a6 a7 1 0 1 0 1 1 1 0 displaystyle a 1 a 0 oplus a 1 oplus a 5 oplus a 6 oplus a 7 oplus 1 0 oplus 1 oplus 0 oplus 1 oplus 1 oplus 1 0 a2 a0 a1 a2 a6 a7 0 0 1 0 1 1 0 1 displaystyle a 2 a 0 oplus a 1 oplus a 2 oplus a 6 oplus a 7 oplus 0 0 oplus 1 oplus 0 oplus 1 oplus 1 oplus 0 1 a3 a0 a1 a2 a3 a7 0 0 1 0 1 1 0 1 displaystyle a 3 a 0 oplus a 1 oplus a 2 oplus a 3 oplus a 7 oplus 0 0 oplus 1 oplus 0 oplus 1 oplus 1 oplus 0 1 a4 a0 a1 a2 a3 a4 0 0 1 0 1 0 0 0 displaystyle a 4 a 0 oplus a 1 oplus a 2 oplus a 3 oplus a 4 oplus 0 0 oplus 1 oplus 0 oplus 1 oplus 0 oplus 0 0 a5 a1 a2 a3 a4 a5 1 1 0 1 0 0 1 1 displaystyle a 5 a 1 oplus a 2 oplus a 3 oplus a 4 oplus a 5 oplus 1 1 oplus 0 oplus 1 oplus 0 oplus 0 oplus 1 1 a6 a2 a3 a4 a5 a6 1 0 1 0 0 1 1 1 displaystyle a 6 a 2 oplus a 3 oplus a 4 oplus a 5 oplus a 6 oplus 1 0 oplus 1 oplus 0 oplus 0 oplus 1 oplus 1 1 a7 a3 a4 a5 a6 a7 0 1 0 0 1 1 0 1 displaystyle a 7 a 3 oplus a 4 oplus a 5 oplus a 6 oplus a 7 oplus 0 1 oplus 0 oplus 0 oplus 1 oplus 1 oplus 0 1 Boylece a y7 y6 y5 y3 y2 1 11101101 ED afin donusumu elde edilir Duzlem geometride Afin donusum Gercek duzlemde basit bir afin donusum ℝ2 icinde donusum tarafindan verilen gonderme ile sag tarafta gerceklestirilen gosterim xy 0121 xy 100 100 displaystyle begin bmatrix x y end bmatrix mapsto begin bmatrix 0 amp 1 2 amp 1 end bmatrix begin bmatrix x y end bmatrix begin bmatrix 100 100 end bmatrix Orijinal ucgen kirmizi uc kose noktalari donusum ile yeni ucgen mavi olusturan uc yeni nokta verir Bu donusum orijinal ucgeni egriltir ve oteler Aslinda her ucgen afin bir donusum baska bir ucgen ile ilgilidir Bu ayni zamanda tum paralelkenarlar icin degil tum dortgenler icin de gecerlidir Ayrica bakinizNotlarBu maddedeki bilgilerin dogrulanabilmesi icin ek kaynaklar gerekli Lutfen guvenilir kaynaklar ekleyerek maddenin gelistirilmesine yardimci olun Kaynaksiz icerik itiraz konusu olabilir ve kaldirilabilir Kaynak ara Afin donusumu haber gazete kitap akademik JSTOR Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin a b Berger Marcel 1987 p 38 Schneider Philip K amp Eberly David H 2003 Geometric Tools for Computer Graphics Morgan Kaufmann s 98 ISBN 978 1 55860 594 7 13 Ekim 2013 tarihinde kaynagindan Erisim tarihi 11 Ekim 2013 Kaynakca 1987 Geometry I Berlin Springer ISBN 3 540 11658 3 Sasaki S 1994 Affine Differential Geometry New bas Cambridge University Press ISBN 978 0 521 44177 3 Sharpe R W 1997 Differential Geometry Cartan s Generalization of Klein s Erlangen Program New York Springer ISBN 0 387 94732 9 Dis baglantilar Hakan Haberdar University of Houston 11 Subat 2015 tarihinde kaynagindan arsivlendi Hazewinkel Michiel Ed 2001 Affine transformation Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Geometric Operations Affine Transform 10 Ekim 2013 tarihinde Wayback Machine sitesinde R Fisher S Perkins A Walker and E Wolfart Eric W Weisstein Affine Transformation MathWorld Affine Transform 12 Ekim 2013 tarihinde Wayback Machine sitesinde by Bernard Vuilleumier Affine Transformation on PlanetMath 1 Mart 2012 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State