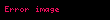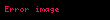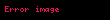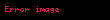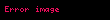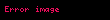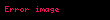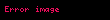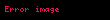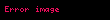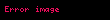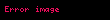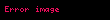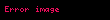İki tane karmaşık birimi olan ya da bir tane hiperbolik iki tane de karmaşık birimi olan kümeye çifte karmaşık sayılar kümesi denir. Bu kümede her sayı
şeklinde ifade edilebilir. Ancak karıştırılmamalıdır. Çünkü bu kümede
iken
olarak tanımlanır. Zira, bu sayılar dörtlük sayıların değişmelisi olarak anılır.
Bu maddede , yâni hiperbolik birim genellikle ile gösterilecektir.
Tanım
Çifte karmaşık sayılar birkaç şekilde tanımlanabilir. En yaygın tanımı iki farklı karmaşık sayı kümesinin birleştirimi olduğu için küme çifte karmaşık sıfatını almıştır.
İki karmaşık birim sayı tanımı
İki farklı karmaşık sayı kümesi olduğunu varsayalım:
ve
.
Yâni biri gerçel sayılardan elde ettiğimiz alışık olduğumuz karmaşık sayılar kümesi, diğeri ise alışık olduğumuz karmaşık sayılardan elde ettiğimiz daha geniş bir halka. Bu kümeye çifte karmaşık sayılar kümesi denir.
O halde, 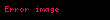
şeklinde yazılabilir. Buradaki iki birimin çarpımı
olarak tanımlanır ve bu sayıya 'hiperbolik birim sayı adı verilir. Açık olarak görülür ki bu birim sayı,
özelliğini sağlar. Bu takdirde her çifte karmaşık sayı,
olarak ifade edilebilir.
Karmaşık katsayılı hiperbolik sayı tanımı
Eğer hiperbolik bir sayının tanımını
gibi karmaşık katsayılı olarak alırsak her çifte karmaşık sayı
şeklinde ifade edilecektir. Burada
ve bu takdirde
olarak tanımlamakla her çifte karmaşık sayıyı
şeklinde ifade etmiş ve istediğimiz özellikleri sağlamış oluruz.
Ayrıca bakınız
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Iki tane karmasik birimi olan ya da bir tane hiperbolik iki tane de karmasik birimi olan kumeye cifte karmasik sayilar kumesi denir Bu kumede her sayi z a e1b e2c e3d displaystyle z a mathbf e 1 b mathbf e 2 c mathbf e 3 d seklinde ifade edilebilir Ancak karistirilmamalidir Cunku bu kumede e12 e22 1 displaystyle mathbf e 1 2 mathbf e 2 2 1 iken e32 1 displaystyle mathbf e 3 2 1 olarak tanimlanir Zira bu sayilar dortluk sayilarin degismelisi olarak anilir Bu maddede e3 displaystyle mathbf e 3 yani hiperbolik birim genellikle h displaystyle mathbf h ile gosterilecektir TanimCifte karmasik sayilar birkac sekilde tanimlanabilir En yaygin tanimi iki farkli karmasik sayi kumesinin birlestirimi oldugu icin kume cifte karmasik sifatini almistir Iki karmasik birim sayi tanimi Iki farkli karmasik sayi kumesi oldugunu varsayalim C1 a i1b a b R ve i12 1 displaystyle mathbb C 1 a mathbf i 1 b a b in mathbb R text ve mathbf i 1 2 1 ve C2 a i2b a b C1 ve i22 1 displaystyle mathbb C 2 a mathbf i 2 b a b in mathbb C 1 text ve mathbf i 2 2 1 Yani biri gercel sayilardan elde ettigimiz alisik oldugumuz karmasik sayilar kumesi digeri ise alisik oldugumuz karmasik sayilardan elde ettigimiz daha genis bir halka Bu kumeye cifte karmasik sayilar kumesi denir O halde C2 displaystyle mathbb C 2 kumesindeki her oge z a i1b i2c i1i2d displaystyle z a mathbf i 1 b mathbf i 2 c mathbf i 1 mathbf i 2 d seklinde yazilabilir Buradaki iki birimin carpimi h i1i2 i2i1 displaystyle mathbf h mathbf i 1 mathbf i 2 mathbf i 2 mathbf i 1 olarak tanimlanir ve bu sayiya hiperbolik birim sayi adi verilir Acik olarak gorulur ki bu birim sayi h2 i1i2 2 i12i22 1 1 1 displaystyle mathbf h 2 mathbf i 1 mathbf i 2 2 mathbf i 1 2 mathbf i 2 2 1 1 1 ozelligini saglar Bu takdirde her cifte karmasik sayi z a i1b i2c hd displaystyle z a mathbf i 1 b mathbf i 2 c mathbf h d olarak ifade edilebilir Karmasik katsayili hiperbolik sayi tanimi Eger hiperbolik bir sayinin tanimini H a hb a b C ve h2 1 displaystyle mathbb H a mathbf h b a b in mathbb C text ve mathbf h 2 1 gibi karmasik katsayili olarak alirsak her cifte karmasik sayi z a ib c id h a ib hc hid displaystyle z a mathbf i b c mathbf i d mathbf h a mathbf i b mathbf h c mathbf h mathbf i d seklinde ifade edilecektir Burada k hi ih displaystyle mathbf k mathbf h mathbf i mathbf i mathbf h ve bu takdirde k2 1 displaystyle mathbf k 2 1 olarak tanimlamakla her cifte karmasik sayiyi z a ib hc kd displaystyle z a mathbf i b mathbf h c mathbf k d seklinde ifade etmis ve istedigimiz ozellikleri saglamis oluruz Ayrica bakinizBolum halkasiMatematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State