İstatistikte, Welch'in t-testi veya eşit olmayan varyanslar t-testi, iki popülasyonun eşit ortalamalara sahip olduğu hipotezini test etmek için kullanılan iki örneklemli bir konum testidir. Welch'in t-testi, Student'ın t-testinin uyarlanmasıdır, Yani, Student'ın t testi yardımıyla türetilmiştir ve iki numunenin eşitsiz varyanslara ve eşit olmayan örneklem boyutlarına sahip olması durumunda daha güvenilirdir. Bu testlere, genellikle, karşılaştırılan iki numunenin altında yatan istatistiksel birimler çakışmaz olduğunda tipik olarak uygulandığı için "eşleştirilmemiş" veya "bağımsız örnekler" "t" testleri olarak adlandırılır.Welch'in t-testinin Student'ın t-testinden daha az popüler olduğu ve okuyuculara daha az tanıdığı göz önüne alındığında, kısaca "Welch'in eşitsiz varyans t-testi" veya "eşitsiz varyans t -testi" daha bilgilendirici bir addır.
Varsayımlar
Student'ın t-testi, iki popülasyonun normal dağılımlara ve eşit varyansa sahip olduğunu varsayar. Welch'in t- testi, eşit olmayan varyanslar için tasarlanmıştır, ancak normalite varsayımı korunmaktadır. Welch'in t-testi, Behrens-Fisher problemi için yaklaşık bir çözümdür.
Aspin ve Welch gibi bazı yazarlar, Welch istatistiklerinde serbestlik derecelerini (df) elde etmek için yöntemler sundular. Keselman ve ark., formüllerin hiçbiri kesinlikle doğru df sağlamaz ve bu nedenle yaklaşık df (ADF) olarak adlandırılırlar. Yaygın olarak kullanılan formül Welch tarafından önerilmiştir. Bu varyans tahmini ile ilişkili serbestlik dereceleri, Welch-Satterthwaite denklemi kullanılarak örnek verilerden yaklaşıklandırılır.
Hesaplamalar
Welch'in t- testi istatistiği t'ni aşağıdaki formüle göre tanımlar:



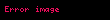
Burada 
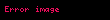
Welch'in t- testi de sıralanan veriler için hesaplanabilir ve daha sonra Welch'in U- testi olarak adlandırılabilir.
İstatistiksel test
T ve 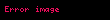
Avantaj ve sınırlamalar
Welch'in t-testi Student'ın t-testinden daha sağlamdır ve eşitsiz varyansların ve eşit olmayan örneklem boyutlarının nominaline yakın tip I hata oranlarını korur.Ayrıca, popülasyon farklılıkları eşit olduğunda ve numune boyutları dengelense bile, Welch'in t-testinin gücü Student'ın t-testinin gücüne yakındır. Welch'in t-testi, tek yönlü varyans analizinden daha sağlam olan 2'den fazla numuneye genellenebilir.
Eşit farklılıkları ön teste tabi tutmak ve daha sonra Student's t-testi veya Welch'in t-testi arasında seçim yapmak tavsiye edilmez. Daha ziyade, Welch'in t-testi, yukarıda belirtildiği gibi doğrudan ve Student'ın t-testine herhangi bir önemli dezavantaj olmadan uygulanabilir. Yer belirleme testinden önce kullanılan eşitliğin eşitliği için yapılan ön testler istatistikçiler tarafından artık yaygın olarak önerilmez; ancak bazı ek kitaplar ve yazılım paketlerinde de geçerlidir. Simülasyonlar, iki aşamalı prosedürün, önem seviyesini korumakta başarısız olduğunu ve genellikle durumun daha da kötüsü ön testlerin sıklıkla testin boyutunu olumsuz etkilediğini ve varyansların eşit olmadığı durumlarda Welch t-testinin Student t-testinden üstün olduğunu göstermiştir. Mevcut simülasyonlar, örneklem boyutları daha küçük olduğunda, varyanslar arasındaki farkın aşırı olmadığından daha hafif olduğu ve anlamlılık seviyesinin daha katı olduğu zaman hata oranlarındaki değişimlerin daha fazla olduğunu ortaya koymaktadır. Dahası, Welch t-testinin geçerliliği, yalnızca bir ön testin gerekli olduğunu belirttiği durumlarda kullanıldığında bozulur. Numune boyutları eşitsiz olduğunda koşulsuz olarak ayrı bir varyans testi kullanılarak optimum koruma sağlanır. Welch'in t-testi çarpık dağılımlar ve büyük örnek boyutları için daha güvenilirdir. Sıralanan dağılımlar ve daha küçük örnekler için güvenilirlik azalır ve burada Welch'in sıralanmış veriler üzerinde t testi yapılabilir.
Örnekler
Aşağıdaki üç örnek Welch'in t-testi ve Student'ın t-testini karşılaştırmaktadır. Örnekler, R programlama dili kullanılarak rastgele normal dağılımlardan alınmıştır.
Üç örnek için de nüfus ortalamaları 

İlk örnek eşit varyans (
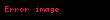
İkinci örnek eşit olmayan varyanslar(



Üçüncü örnek eşit olmayan varyanslar (
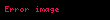


Referans p-değerleri, eşit popülasyon araçlarının boş hipotez için (
| Sample A1 | Sample A2 | Student's t-test | Welch's t-test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Example |  |  |  |  |  |  |  | 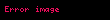 |  |  |  | 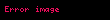 |  |  |
| 1 | 15 | 20.8 | 7.9 | 15 | 23.0 | 3.8 | −2.46 | 28 | 0.021 | 0.021 | −2.46 | 25.0 | 0.021 | 0.017 |
| 2 | 10 | 20.6 | 9.0 | 20 | 22.1 | 0.9 | −2.10 | 28 | 0.045 | 0.150 | −1.57 | 9.9 | 0.149 | 0.144 |
| 3 | 10 | 19.4 | 1.4 | 20 | 21.6 | 17.1 | −1.64 | 28 | 0.110 | 0.036 | −2.22 | 24.5 | 0.036 | 0.042 |
Welch'in t - testi ve Student'ın t - testi, eşit varyans ve eşit örnek büyüklüğüne sahip iki örnek için pratik olarak aynı sonuçları verdi (Örnek 1). Eşit olmayan varyanslar için, Student'in t- testi, küçük örneklemin daha büyük bir varyansa (Örnek 2) ve daha büyük bir örneğin daha büyük bir varyansa sahip olduğu (örnek 3) yüksek bir p-değeri verdi. Eşit olmayan varyanslar için, Welch'in t- testi, simüle edilen p-değerlerine yakın p-değerleri verdi.
Yazılım Uygulamaları
| Language/Program | Function | Notes |
|---|---|---|
| LibreOffice | TTEST(Data1; Data2; Mode; Type) | See [1]28 Şubat 2014 tarihinde Wayback Machine sitesinde . |
| MATLAB | ttest2(data1, data2, 'Vartype', 'unequal') | See [2] 5 Ağustos 2016 tarihinde Wayback Machine sitesinde . |
| Microsoft Excel pre 2010 | TTEST(array1, array2, tails, type) | See |
| Microsoft Excel 2010 and later | T.TEST(array1, array2, tails, type) | See [4]3 Mart 2014 tarihinde Wayback Machine sitesinde . |
| Python | scipy.stats.ttest_ind(a, b, axis=0, equal_var=False) | See [5]23 Ekim 2013 tarihinde Wayback Machine sitesinde . |
t.test(data1, data2, alternative="two.sided", var.equal=FALSE) | See [6] 29 Kasım 2016 tarihinde Wayback Machine sitesinde . | |
UnequalVarianceTTest(data1, data2) | See [7] 29 Mart 2016 tarihinde Wayback Machine sitesinde . | |
| ttest varname1 == varname2, welch | See 8 7 Ocak 2010 tarihinde Wayback Machine sitesinde . |
Ayrıca bakınız
Kaynakça
- ^ a b Welch, B. L. (1947). "The generalization of "Student's" problem when several different population variances are involved". . 34 (1–2). ss. 28-35. doi:10.1093/biomet/34.1-2.28. MR 0019277.
- ^ a b c Ruxton, G. D. (2006). "The unequal variance t-test is an underused alternative to Student's t-test and the Mann–Whitney U test". Behavioral Ecology. Cilt 17. ss. 688-690. doi:10.1093/beheco/ark016.
- ^ Ahad, Nor Aishah; Yahaya, Sharipah Soaad Syed (2014). Sensitivity Analysis of Welch’s t -Test. AIP Publishing LLC. ss. 888-893.
- ^ a b Fagerland, M. W.; Sandvik, L. (2009). "Performance of five two-sample location tests for skewed distributions with unequal variances". . Cilt 30. ss. 490-496. doi:10.1016/j.cct.2009.06.007.
- ^ Welch, B. L. (1951). "On the Comparison of Several Mean Values: An Alternative Approach". Biometrika. Cilt 38. ss. 330-336. doi:10.2307/2332579. JSTOR 2332579.
- ^ Zimmerman, D. W. (2004). "A note on preliminary tests of equality of variances". . Cilt 57. ss. 173-181. doi:10.1348/000711004849222.
- ^ Fagerland, M. W. (2012). "t-tests, non-parametric tests, and large studies—a paradox of statistical practice?". BioMed Central Medical Research Methodology. Cilt 12. s. 78. doi:10.1186/1471-2288-12-78.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Istatistikte Welch in t testi veya esit olmayan varyanslar t testi iki populasyonun esit ortalamalara sahip oldugu hipotezini test etmek icin kullanilan iki orneklemli bir konum testidir Welch in t testi Student in t testinin uyarlanmasidir Yani Student in t testi yardimiyla turetilmistir ve iki numunenin esitsiz varyanslara ve esit olmayan orneklem boyutlarina sahip olmasi durumunda daha guvenilirdir Bu testlere genellikle karsilastirilan iki numunenin altinda yatan istatistiksel birimler cakismaz oldugunda tipik olarak uygulandigi icin eslestirilmemis veya bagimsiz ornekler t testleri olarak adlandirilir Welch in t testinin Student in t testinden daha az populer oldugu ve okuyuculara daha az tanidigi goz onune alindiginda kisaca Welch in esitsiz varyans t testi veya esitsiz varyans t testi daha bilgilendirici bir addir VarsayimlarStudent in t testi iki populasyonun normal dagilimlara ve esit varyansa sahip oldugunu varsayar Welch in t testi esit olmayan varyanslar icin tasarlanmistir ancak normalite varsayimi korunmaktadir Welch in t testi Behrens Fisher problemi icin yaklasik bir cozumdur Aspin ve Welch gibi bazi yazarlar Welch istatistiklerinde serbestlik derecelerini df elde etmek icin yontemler sundular Keselman ve ark formullerin hicbiri kesinlikle dogru df saglamaz ve bu nedenle yaklasik df ADF olarak adlandirilirlar Yaygin olarak kullanilan formul Welch tarafindan onerilmistir Bu varyans tahmini ile iliskili serbestlik dereceleri Welch Satterthwaite denklemi kullanilarak ornek verilerden yaklasiklandirilir HesaplamalarWelch in t testi istatistigi t ni asagidaki formule gore tanimlar t X 1 X 2s12N1 s22N2 displaystyle t quad quad overline X 1 overline X 2 over sqrt s 1 2 over N 1 s 2 2 over N 2 quad X 1 displaystyle overline X 1 s12 displaystyle s 1 2 and N1 displaystyle N 1 sirasiyla birinci ornek ortalamasi ornek varyansi ve ornek buyuklugudur Student in t testinden farkli olarak payda birlestirilmis varyans tahmine dayali degildir Bu varyans tahminiyle iliskili serbestlik dereceleri n displaystyle nu Welch Satterthwaite denklemi kullanilarak yaklastirilir n s12N1 s22N2 2s14N12n1 s24N22n2 displaystyle nu quad approx quad left s 1 2 over N 1 s 2 2 over N 2 right 2 over quad s 1 4 over N 1 2 nu 1 s 2 4 over N 2 2 nu 2 quad Burada n1 N1 1 displaystyle nu 1 N 1 1 ilk varyans tahmini ile iliskili serbestlik derecelerini n2 N2 1 displaystyle nu 2 N 2 1 ikinci varyans tahminiyle iliskili serbestlik derecelerini ifade etmektedir Welch in t testi de siralanan veriler icin hesaplanabilir ve daha sonra Welch in U testi olarak adlandirilabilir Istatistiksel testT ve n displaystyle nu hesaplandiktan sonra bu istatistikler iki populasyon ortalamasinin esit oldugu iki uclu test kullanilarak bos hipotezi test etmek icin t dagilimi ile veya populasyon ortalamalarinin birinin Digerinden buyuk veya esit tek kuyruklu test kullanarak oldugu alternatif hipotezler icin kullanilabilir Avantaj ve sinirlamalarWelch in t testi Student in t testinden daha saglamdir ve esitsiz varyanslarin ve esit olmayan orneklem boyutlarinin nominaline yakin tip I hata oranlarini korur Ayrica populasyon farkliliklari esit oldugunda ve numune boyutlari dengelense bile Welch in t testinin gucu Student in t testinin gucune yakindir Welch in t testi tek yonlu varyans analizinden daha saglam olan 2 den fazla numuneye genellenebilir Esit farkliliklari on teste tabi tutmak ve daha sonra Student s t testi veya Welch in t testi arasinda secim yapmak tavsiye edilmez Daha ziyade Welch in t testi yukarida belirtildigi gibi dogrudan ve Student in t testine herhangi bir onemli dezavantaj olmadan uygulanabilir Yer belirleme testinden once kullanilan esitligin esitligi icin yapilan on testler istatistikciler tarafindan artik yaygin olarak onerilmez ancak bazi ek kitaplar ve yazilim paketlerinde de gecerlidir Simulasyonlar iki asamali prosedurun onem seviyesini korumakta basarisiz oldugunu ve genellikle durumun daha da kotusu on testlerin siklikla testin boyutunu olumsuz etkiledigini ve varyanslarin esit olmadigi durumlarda Welch t testinin Student t testinden ustun oldugunu gostermistir Mevcut simulasyonlar orneklem boyutlari daha kucuk oldugunda varyanslar arasindaki farkin asiri olmadigindan daha hafif oldugu ve anlamlilik seviyesinin daha kati oldugu zaman hata oranlarindaki degisimlerin daha fazla oldugunu ortaya koymaktadir Dahasi Welch t testinin gecerliligi yalnizca bir on testin gerekli oldugunu belirttigi durumlarda kullanildiginda bozulur Numune boyutlari esitsiz oldugunda kosulsuz olarak ayri bir varyans testi kullanilarak optimum koruma saglanir Welch in t testi carpik dagilimlar ve buyuk ornek boyutlari icin daha guvenilirdir Siralanan dagilimlar ve daha kucuk ornekler icin guvenilirlik azalir ve burada Welch in siralanmis veriler uzerinde t testi yapilabilir OrneklerAsagidaki uc ornek Welch in t testi ve Student in t testini karsilastirmaktadir Ornekler R programlama dili kullanilarak rastgele normal dagilimlardan alinmistir Uc ornek icin de nufus ortalamalari m1 20 displaystyle mu 1 20 and m2 22 displaystyle mu 2 22 dir Ilk ornek esit varyans s12 s22 4 displaystyle sigma 1 2 sigma 2 2 4 ve esit ornek buyuklukleri N1 N2 15 displaystyle N 1 N 2 15 icindir iki rassal numuneyi A1 ve A2 olarak belirtelim A1 27 5 21 0 19 0 23 6 17 0 17 9 16 9 20 1 21 9 22 6 23 1 19 6 19 0 21 7 21 4 displaystyle A 1 27 5 21 0 19 0 23 6 17 0 17 9 16 9 20 1 21 9 22 6 23 1 19 6 19 0 21 7 21 4 A2 27 1 22 0 20 8 23 4 23 4 23 5 25 8 22 0 24 8 20 2 21 9 22 1 22 9 20 5 24 4 displaystyle A 2 27 1 22 0 20 8 23 4 23 4 23 5 25 8 22 0 24 8 20 2 21 9 22 1 22 9 20 5 24 4 Ikinci ornek esit olmayan varyanslar s12 16 displaystyle sigma 1 2 16 s22 1 displaystyle sigma 2 2 1 ve esit olmayan ornek buyuklukleri icindir N1 10 displaystyle N 1 10 N2 20 displaystyle N 2 20 Kucuk ornek daha buyuk varyansa sahiptir A1 17 2 20 9 22 6 18 1 21 7 21 4 23 5 24 2 14 7 21 8 A2 21 5 22 8 21 0 23 0 21 6 23 6 22 5 20 7 23 4 21 8 20 7 21 7 21 5 22 5 23 6 21 5 22 5 23 5 21 5 21 8 displaystyle begin aligned A 1 amp 17 2 20 9 22 6 18 1 21 7 21 4 23 5 24 2 14 7 21 8 A 2 amp 21 5 22 8 21 0 23 0 21 6 23 6 22 5 20 7 23 4 21 8 20 7 21 7 21 5 22 5 23 6 21 5 22 5 23 5 21 5 21 8 end aligned Ucuncu ornek esit olmayan varyanslar s12 1 displaystyle sigma 1 2 1 s22 16 displaystyle sigma 2 2 16 ve esit olmayan ornek boyutlari icindir N1 10 displaystyle N 1 10 N2 20 displaystyle N 2 20 Buyuk orneklemin daha buyuk varyansi vardir A1 19 8 20 4 19 6 17 8 18 5 18 9 18 3 18 9 19 5 22 0 A2 28 2 26 6 20 1 23 3 25 2 22 1 17 7 27 6 20 6 13 7 23 2 17 5 20 6 18 0 23 9 21 6 24 3 20 4 24 0 13 2 displaystyle begin aligned A 1 amp 19 8 20 4 19 6 17 8 18 5 18 9 18 3 18 9 19 5 22 0 A 2 amp 28 2 26 6 20 1 23 3 25 2 22 1 17 7 27 6 20 6 13 7 23 2 17 5 20 6 18 0 23 9 21 6 24 3 20 4 24 0 13 2 end aligned Referans p degerleri esit populasyon araclarinin bos hipotez icin m1 m2 0 displaystyle mu 1 mu 2 0 t istatistiklerinin dagilimlarini simule ederek elde edildi Sonuclar asagidaki tabloda cift kuyruklu p degerleri ile ozetlenmistir Sample A1 Sample A2 Student s t test Welch s t testExample N1 displaystyle N 1 X 1 displaystyle overline X 1 s12 displaystyle s 1 2 N2 displaystyle N 2 X 2 displaystyle overline X 2 s22 displaystyle s 2 2 t displaystyle t n displaystyle nu P displaystyle P Psim displaystyle P mathrm sim t displaystyle t n displaystyle nu P displaystyle P Psim displaystyle P mathrm sim 1 15 20 8 7 9 15 23 0 3 8 2 46 28 0 021 0 021 2 46 25 0 0 021 0 0172 10 20 6 9 0 20 22 1 0 9 2 10 28 0 045 0 150 1 57 9 9 0 149 0 1443 10 19 4 1 4 20 21 6 17 1 1 64 28 0 110 0 036 2 22 24 5 0 036 0 042 Welch in t testi ve Student in t testi esit varyans ve esit ornek buyuklugune sahip iki ornek icin pratik olarak ayni sonuclari verdi Ornek 1 Esit olmayan varyanslar icin Student in t testi kucuk orneklemin daha buyuk bir varyansa Ornek 2 ve daha buyuk bir ornegin daha buyuk bir varyansa sahip oldugu ornek 3 yuksek bir p degeri verdi Esit olmayan varyanslar icin Welch in t testi simule edilen p degerlerine yakin p degerleri verdi Yazilim UygulamalariLanguage Program Function NotesLibreOffice TTEST i Data1 Data2 Mode Type i See 1 28 Subat 2014 tarihinde Wayback Machine sitesinde MATLAB ttest2 data1 data2 Vartype unequal See 2 5 Agustos 2016 tarihinde Wayback Machine sitesinde Microsoft Excel pre 2010 TTEST i array1 i i array2 i i tails i i type i SeeMicrosoft Excel 2010 and later T TEST i array1 i i array2 i i tails i i type i See 4 3 Mart 2014 tarihinde Wayback Machine sitesinde Python scipy stats ttest ind i a i i b i i axis 0 i i equal var False i See 5 23 Ekim 2013 tarihinde Wayback Machine sitesinde t test data1 data2 alternative two sided var equal FALSE See 6 29 Kasim 2016 tarihinde Wayback Machine sitesinde UnequalVarianceTTest data1 data2 See 7 29 Mart 2016 tarihinde Wayback Machine sitesinde ttest varname1 varname2 welch See 8 7 Ocak 2010 tarihinde Wayback Machine sitesinde Ayrica bakinizStudent in t testiKaynakca a b Welch B L 1947 The generalization of Student s problem when several different population variances are involved 34 1 2 ss 28 35 doi 10 1093 biomet 34 1 2 28 MR 0019277 a b c Ruxton G D 2006 The unequal variance t test is an underused alternative to Student s t test and the Mann Whitney U test Behavioral Ecology Cilt 17 ss 688 690 doi 10 1093 beheco ark016 Ahad Nor Aishah Yahaya Sharipah Soaad Syed 2014 Sensitivity Analysis of Welch s t Test AIP Publishing LLC ss 888 893 a b Fagerland M W Sandvik L 2009 Performance of five two sample location tests for skewed distributions with unequal variances Cilt 30 ss 490 496 doi 10 1016 j cct 2009 06 007 Welch B L 1951 On the Comparison of Several Mean Values An Alternative Approach Biometrika Cilt 38 ss 330 336 doi 10 2307 2332579 JSTOR 2332579 Zimmerman D W 2004 A note on preliminary tests of equality of variances Cilt 57 ss 173 181 doi 10 1348 000711004849222 Fagerland M W 2012 t tests non parametric tests and large studies a paradox of statistical practice BioMed Central Medical Research Methodology Cilt 12 s 78 doi 10 1186 1471 2288 12 78
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State