Bu madde Vektör Analizi'ndeki önemli özdeşlikleri içermektedir.
Operatörlerin Notasyonu
Gradyan
Ana madde:Gradyan
3 boyutlu kartezyen koordinatlarında verilen 3 değişkenli 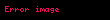
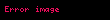

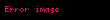
Burada 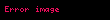

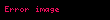




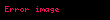
Genellersek herhangi bir k ranklı bir 
Diverjans
Ana madde:Diverjans
Kartezyen koordinatlarında sürekli ve türevlenebilir bir 
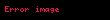
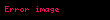
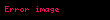

Gradyanda olan mantık burada da geçerlidir.Yani k boyutlu bir 

Rotasyonel
Ana madde;Rotasyonel
Kartezyen koordinat sisteminde bir 
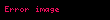

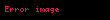
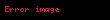
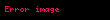
Vektör ya da daha genel anlamda tensörlerin rotasyoneli esas alınarak tensör dili ile yazılabilir;


Burada 
Laplasyen
Ana Madde:Laplace Operatörü
Kartezyen koordinatlarında skaler değerli bir 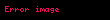
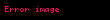
Genel anlamda 

bakımından tensöre bu operatör uygulandığında tensörün rankı değişmeyecektir. Fonksiyonun laplasyeni 0'a eşit ise fonksiyon özel bir fonksiyon olan harmonik fonksiyon niteliğine sahip olur.
İlk Türev Özdeşlikleri
Notasyon bakımından skaler alanlar için 



Dağılma Özellikleri
Skaler ile Çarpılırken Çarpım Kuralı
Tek değişkenli klasik kalkülüsten bildiğimiz çarpım kuralını burada da genelleştirebiliriz.
Skalere bölünürken Bölme Kuralı
İkinci Türev Özdeşlikleri
Rotasyonelin diverjansı sıfıra eşittir
Bir 

Gradyanın diverjansı Laplasyen operatörüne eşittir
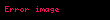
Diverjansın diverjansı tanımsızdır

Sebebi diverjansı alınan vektör skaler olacağı için tekrar diverjans alınamaz.
Not=Bu durum sadece vektörler için geçerlidir.
Gradyanın rotasyoneli sıfıra eşittir
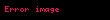
Rotasyonelin rotasyoneli vektör Laplasyeni'ne eşittir
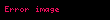
Diverjansın rotasyoneli tanımsızdır
Sebebi diverjansı alınan vektörün skalere dönüştüğünü düşündüğümüzde yeni skalerin rotasyonelinin alınamayacağıdır.
Önemli Özdeşliklerin Özeti
Diferansiyasyon
Gradyan
Diverjans
Rotasyonel
İkinci Türev
(skaler laplasyen)
(vektör laplasyen)
(Green vektör özdeşliği)
Üçüncü Türev
İntegrasyon
''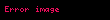
Yüzey-Hacim İntegralleri
Yüzey-Hacim İntegral teoremlerini takip ettiğinizde genelde 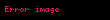
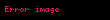
(Diverjans teoremi)
()
Bir eğri üstündeki çizgi integrali
Burada şu anlaşılmalıdır ki saat yönü negatif taraftır ve saat yönünün tersi üzerinde alınan integral saat yönünde alınan integralin negatifine eşittir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vektor Analizi ndeki onemli ozdeslikleri icermektedir Operatorlerin NotasyonuGradyan Ana madde Gradyan 3 boyutlu kartezyen koordinatlarinda verilen 3 degiskenli f x y z displaystyle f x y z fonksiyonunun gradyani bir vektor alani verecektir Notasyon olarak grad f displaystyle grad f veya f displaystyle nabla f ile gosterilir f x y z f displaystyle nabla f partial over partial x partial over partial y partial over partial z f f xi f yj displaystyle partial f over partial x widehat i partial f over partial y widehat j f zk displaystyle partial f over partial z widehat k olarak ifade edilir Goruldugu uzere elde artik 3 boyutlu bir vektor alani vardir Burada i j k displaystyle widehat i widehat j widehat k x y ve z eksenlerini temsil eden birim baz vektorlerdir Genel bir bicimde dusundugumuzde n degiskenli bir 3 x1 x2 xn displaystyle xi x 1 x 2 x n skaler fonksiyonu ele alirsak bu fonksiyonun gradyani bize bir n boyutlu bir vektor alani verecektir 3 x1 x2 xn displaystyle nabla xi partial over partial x 1 partial over partial x 2 partial over partial x n 3 displaystyle xi 3 x1 e 1 3 x2 e 2 displaystyle partial xi over partial x 1 widehat e 1 partial xi over partial x 2 widehat e 2 3 xn e n displaystyle partial xi over partial x n widehat e n 1 n displaystyle 1 times n satir matris formunda yazilan ya da ranki 1 olan tensor yani vektor A displaystyle vec A A1 A2 An displaystyle A 1 A 2 A n gibi bir vektor alani icin gradyan ya da n n displaystyle n times n Jacobian matrisi ile temsil edilir A JA Ai xj ij displaystyle nabla vec A J vec A partial A i over partial x j ij Genellersek herhangi bir k rankli bir A displaystyle A tensorunun gradyani k 1 degerinde bir tensor alani verir Diverjans Ana madde Diverjans Kartezyen koordinatlarinda surekli ve turevlenebilir bir F displaystyle F vektor alaninin diverjansi bir skaler degerli fonksiyon verecektir Notasyon olarak div F displaystyle div F veya F displaystyle nabla cdot F ile temsil edilir F displaystyle nabla cdot F div F x y z displaystyle div F partial over partial x partial over partial y partial over partial z cdot Fx Fy Fz Fx x Fy y displaystyle F x F y F z partial F x over partial x partial F y over partial y Fz z displaystyle partial F z over partial z olarak ifade edilir Gradyanda olan mantik burada da gecerlidir Yani k boyutlu bir A displaystyle A tensor alaninin diverjansi A displaystyle nabla cdot A k 1 boyutlu bir verir Rotasyonel Ana madde Rotasyonel Kartezyen koordinat sisteminde bir F displaystyle F vektor alaninin rotasyoneli yine bir vektor alani verir Notasyon olarak rot F displaystyle rot F ya da F displaystyle nabla times F ile temsil edilir rot F F ijk x y zFxFyFz displaystyle rot F nabla times mathbf F begin vmatrix mathbf i amp mathbf j amp mathbf k frac partial partial x amp frac partial partial y amp frac partial partial z F x amp F y amp F z end vmatrix Fz y Fy z i Fx z Fz x j Fy x Fx y k displaystyle left frac partial F z partial y frac partial F y partial z right mathbf i left frac partial F x partial z frac partial F z partial x right mathbf j left frac partial F y partial x frac partial F x partial y right mathbf k olarak ifade edilir Burada i j k displaystyle mathbf i mathbf j mathbf k x y ve z koordinat eksenlerini temsil eden birim baz vektorlerdir Vektor ya da daha genel anlamda tensorlerin rotasyoneli esas alinarak tensor dili ile yazilabilir F displaystyle F vektor alaninin rotasyoneli F displaystyle nabla times F eijkei Fk xj displaystyle varepsilon ijk e i partial F k over partial x j Burada e displaystyle varepsilon dur Laplasyen Ana Madde Laplace Operatoru Kartezyen koordinatlarinda skaler degerli bir f x y z displaystyle f x y z fonksiyonunun laplasyeni Df 2f f 2f x2 2f y2 displaystyle Delta f nabla 2 f nabla cdot nabla f partial 2 f over partial x 2 partial 2 f over partial y 2 2f z2 displaystyle partial 2 f over partial z 2 Genel anlamda T displaystyle T tensorunun laplasyeni soyle yazilabilir DT 2T T displaystyle Delta T nabla 2 T nabla cdot nabla T bakimindan tensore bu operator uygulandiginda tensorun ranki degismeyecektir Fonksiyonun laplasyeni 0 a esit ise fonksiyon ozel bir fonksiyon olan harmonik fonksiyon niteligine sahip olur Ilk Turev OzdeslikleriNotasyon bakimindan skaler alanlar icin ϕ displaystyle phi ve ps displaystyle psi vektor alanlari icin A displaystyle A ve B displaystyle B kullanacagiz Dagilma Ozellikleri ps ϕ ps ϕ displaystyle nabla psi phi nabla psi nabla phi A B A B displaystyle nabla A B nabla A nabla B A B displaystyle nabla cdot A B A B displaystyle nabla cdot A nabla cdot B A B A B displaystyle nabla times A B nabla times A nabla times B Skaler ile Carpilirken Carpim Kurali Tek degiskenli klasik kalkulusten bildigimiz carpim kuralini burada da genellestirebiliriz psϕ ϕ ps ps ϕ displaystyle nabla psi phi phi nabla psi psi nabla phi psA ps TA ps A ps A ps A displaystyle nabla psi A nabla psi T A psi nabla A nabla psi otimes A psi nabla A psA ps A A ps displaystyle nabla cdot psi mathbf A psi nabla cdot mathbf A mathbf A cdot nabla psi psA ps A ps A displaystyle nabla times psi mathbf A psi nabla times mathbf A nabla psi times mathbf A 2 psϕ ps 2ϕ 2 ps ϕ ϕ 2ps displaystyle nabla 2 psi phi psi nabla 2 phi 2 nabla psi cdot nabla phi phi nabla 2 psi Skalere bolunurken Bolme Kurali fg g f g fg2 displaystyle nabla left frac f g right frac g nabla f nabla g f g 2 Ag g A g Ag2 displaystyle nabla cdot left frac mathbf A g right frac g nabla cdot mathbf A nabla g cdot mathbf A g 2 Ag g A g Ag2 displaystyle nabla times left frac mathbf A g right frac g nabla times mathbf A nabla g times mathbf A g 2 Ikinci Turev OzdeslikleriRotasyonelin diverjansi sifira esittir Bir ϕ displaystyle phi vektorun rotasyonelinin diverjansi sifirdir ϕ 0 displaystyle nabla cdot nabla times phi 0 Gradyanin diverjansi Laplasyen operatorune esittir 2ps ps displaystyle nabla 2 psi nabla cdot nabla psi Diverjansin diverjansi tanimsizdir ps displaystyle nabla cdot nabla cdot psi Tanimsiz Sebebi diverjansi alinan vektor skaler olacagi icin tekrar diverjans alinamaz Not Bu durum sadece vektorler icin gecerlidir Gradyanin rotasyoneli sifira esittir ϕ 0 displaystyle nabla times nabla phi mathbf 0 Rotasyonelin rotasyoneli vektor Laplasyeni ne esittir A A 2A displaystyle nabla times left nabla times mathbf A right nabla nabla cdot mathbf A nabla 2 mathbf A Diverjansin rotasyoneli tanimsizdir Sebebi diverjansi alinan vektorun skalere donustugunu dusundugumuzde yeni skalerin rotasyonelinin alinamayacagidir A displaystyle nabla times nabla cdot A TanimsizOnemli Ozdesliklerin OzetiDiferansiyasyon Gradyan ps ϕ ps ϕ displaystyle nabla psi phi nabla psi nabla phi psϕ ϕ ps ps ϕ displaystyle nabla psi phi phi nabla psi psi nabla phi A B A B B A A B B A displaystyle nabla left mathbf A cdot mathbf B right left mathbf A cdot nabla right mathbf B left mathbf B cdot nabla right mathbf A mathbf A times left nabla times mathbf B right mathbf B times left nabla times mathbf A right Diverjans A B A B displaystyle nabla cdot mathbf A mathbf B nabla cdot mathbf A nabla cdot mathbf B psA ps A A ps displaystyle nabla cdot left psi mathbf A right psi nabla cdot mathbf A mathbf A cdot nabla psi A B B A A B displaystyle nabla cdot left mathbf A times mathbf B right mathbf B cdot nabla times mathbf A mathbf A cdot nabla times mathbf B Rotasyonel A B A B displaystyle nabla times mathbf A mathbf B nabla times mathbf A nabla times mathbf B psA ps A ps A displaystyle nabla times left psi mathbf A right psi nabla times mathbf A nabla psi times mathbf A A B A B B A B A A B displaystyle nabla times left mathbf A times mathbf B right mathbf A left nabla cdot mathbf B right mathbf B left nabla cdot mathbf A right left mathbf B cdot nabla right mathbf A left mathbf A cdot nabla right mathbf B Ikinci Turev A 0 displaystyle nabla cdot nabla times mathbf A 0 ps 0 displaystyle nabla times nabla psi mathbf 0 ps 2ps displaystyle nabla cdot nabla psi nabla 2 psi skaler laplasyen A A 2A displaystyle nabla left nabla cdot mathbf A right nabla times left nabla times mathbf A right nabla 2 mathbf A vektor laplasyen ϕ ps ϕ 2ps ϕ ps displaystyle nabla cdot phi nabla psi phi nabla 2 psi nabla phi cdot nabla psi ps 2ϕ ϕ 2ps ps ϕ ϕ ps displaystyle psi nabla 2 phi phi nabla 2 psi nabla cdot left psi nabla phi phi nabla psi right 2 ϕps ϕ 2ps 2 ϕ ps ps 2ϕ displaystyle nabla 2 phi psi phi nabla 2 psi 2 nabla phi cdot nabla psi psi nabla 2 phi 2 psA A 2ps 2 ps A ps 2A displaystyle nabla 2 psi mathbf A mathbf A nabla 2 psi 2 nabla psi cdot nabla mathbf A psi nabla 2 mathbf A 2 A B A 2B B 2A 2 B A B A displaystyle nabla 2 mathbf A cdot mathbf B mathbf A cdot nabla 2 mathbf B mathbf B cdot nabla 2 mathbf A 2 nabla cdot mathbf B cdot nabla mathbf A mathbf B times nabla times mathbf A Green vektor ozdesligi Ucuncu Turev 2 ps ps 2ps displaystyle nabla 2 nabla psi nabla nabla cdot nabla psi nabla nabla 2 psi 2 A A 2A displaystyle nabla 2 nabla cdot mathbf A nabla cdot nabla nabla cdot mathbf A nabla cdot nabla 2 mathbf A 2 A A 2A displaystyle nabla 2 nabla times mathbf A nabla times nabla times nabla times mathbf A nabla times nabla 2 mathbf A Integrasyon displaystyle partial sembolu burada bir yuzeyin sinirlarini ifade eder Yuzey Hacim Integralleri Yuzey Hacim Integral teoremlerini takip ettiginizde genelde A displaystyle partial A sembolu gorursunuz Bunun anlami eger A 3 boyutlu bir cokkatli ise A displaystyle partial A sinirlarini yani 2 boyutlu bir yuzeyi temsil eder V displaystyle int int partial V bigcirc A dS V A dV displaystyle mathbf A cdot d mathbf S iiint V left nabla cdot mathbf A right dV Diverjans teoremi V displaystyle int int partial V bigcirc psdS V psdV displaystyle psi d mathbf S iiint V nabla psi dV V displaystyle int int partial V bigcirc n A dS V A dV displaystyle left hat mathbf n times mathbf A right dS iiint V left nabla times mathbf A right dV V displaystyle int int partial V bigcirc ps f n dS V ps 2f f ps dV displaystyle psi left nabla varphi cdot hat mathbf n right dS iiint V left psi nabla 2 varphi nabla varphi cdot nabla psi right dV V displaystyle int int partial V bigcirc ps f f ps n dS G displaystyle left left psi nabla varphi varphi nabla psi right cdot hat mathbf n right dS G G V displaystyle G int int partial V bigcirc ps f n f ps n dS displaystyle left psi frac partial varphi partial n varphi frac partial psi partial n right dS V ps 2f f 2ps dV displaystyle displaystyle iiint V left psi nabla 2 varphi varphi nabla 2 psi right dV Bir egri ustundeki cizgi integrali SA dℓ S A ds displaystyle oint partial S mathbf A cdot d boldsymbol ell iint S left nabla times mathbf A right cdot d mathbf s Stokes Teoremi Spsdℓ S n ps dS displaystyle oint partial S psi d boldsymbol ell iint S left hat mathbf n times nabla psi right dS Burada su anlasilmalidir ki saat yonu negatif taraftir ve saat yonunun tersi uzerinde alinan integral saat yonunde alinan integralin negatifine esittir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State