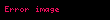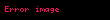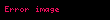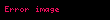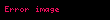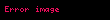Ayrık tekdüze dağılım (İngilizce discrete uniform distribution), olasılık kuramı ve istatistik bilim kollarında, bir rassal değişken için belirli bir alt ve üst sınır tam sayı arasında mümkün olan bir sıra tam sayı sonuç değerlerin hepsinin eşit ölçüde olasılık göstermesi özelliğini taşıyan .
Olasılık kütle fonksiyonu n=5 eger n=b-a+1 | |
Yığmalı dağılım fonksiyonu | |
| Parametreler | |
|---|---|
| Olasılık kütle fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | N/A |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | |
| Karakteristik fonksiyon | |
Eğer bir rassal değişken için şekilde herhangi mümkün değerin her biri eşit olasılık gösteriyorsa, bu rassal değişken ayrık tekdüze dağılım gösterir demektir. Bu şekilde herhangi bir olay için olasılık olur. Bu ayrık tekdüze dağılım için basit bir örneğin, hilesi olmayan bir zarın tek defa atımı sonucudur. için olanaklı değerler 1, 2, 3, 4, 5,6 olup zarın her atılışında belirlenmiş bir sayı gelmesi için olasılık 1/6dir.
Eğer ayrık tekdüze dağılımı özelliği olan bir rassal değişken için değerler reel ise, yığmalı dağılım fonksiyonu bozulmuş dağılım şeklinde ifade şöyle verilebilir:
Burada Heaviside tipi bir olup değerde merkezlenen bir bozulmuş dağılım için bir yığmalı dağılım fonksiyonudur. Bu ifadeyi elde etmek için geçiş noktalarının hesaplanmasında tutarlı usuller kullanıldığı kabul edilmektedir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Ayrik tekduze dagilim Ingilizce discrete uniform distribution olasilik kurami ve istatistik bilim kollarinda bir rassal degisken icin belirli bir alt ve ust sinir tam sayi arasinda mumkun olan bir sira tam sayi sonuc degerlerin hepsinin esit olcude olasilik gostermesi ozelligini tasiyan Ayrik tekduze Olasilik kutle fonksiyonu n 5 eger n b a 1Yigmali dagilim fonksiyonuParametreler a 2 1 0 1 2 displaystyle a in dots 2 1 0 1 2 dots b 2 1 0 1 2 displaystyle b in dots 2 1 0 1 2 dots n b a 1 displaystyle n b a 1 k a a 1 b 1 b displaystyle k in a a 1 dots b 1 b Olasilik kutle fonksiyonu OYF 1neger a k b 0diger hallerde displaystyle begin matrix frac 1 n amp mbox eger a leq k leq b 0 amp mbox diger hallerde end matrix Birikimli dagilim fonksiyonu YDF 0eger k lt a k a 1neger a k b1eger k gt b displaystyle begin matrix 0 amp mbox eger k lt a frac lfloor k rfloor a 1 n amp mbox eger a leq k leq b 1 amp mbox eger k gt b end matrix Ortalama a b2 displaystyle frac a b 2 Medyan a b2 displaystyle frac a b 2 Mod N AVaryans n2 112 displaystyle frac n 2 1 12 Carpiklik 0 displaystyle 0 Fazladan basiklik 6 n2 1 5 n2 1 displaystyle frac 6 n 2 1 5 n 2 1 Entropi ln n displaystyle ln n Moment ureten fonksiyon mf eat e b 1 tn 1 et displaystyle frac e at e b 1 t n 1 e t Karakteristik fonksiyon eiat ei b 1 tn 1 eit displaystyle frac e iat e i b 1 t n 1 e it Eger bir rassal degisken icin k1 k2 kn displaystyle k 1 k 2 dots k n sekilde herhangi n displaystyle n mumkun degerin her biri esit olasilik gosteriyorsa bu rassal degisken ayrik tekduze dagilim gosterir demektir Bu sekilde herhangi bir olay ki displaystyle k i icin olasilik 1 n displaystyle 1 n olur Bu ayrik tekduze dagilim icin basit bir ornegin hilesi olmayan bir zarin tek defa atimi sonucudur k displaystyle k icin olanakli degerler 1 2 3 4 5 6 olup zarin her atilisinda belirlenmis bir sayi gelmesi icin olasilik 1 6dir Eger ayrik tekduze dagilimi ozelligi olan bir rassal degisken icin degerler reel ise yigmali dagilim fonksiyonu bozulmus dagilim seklinde ifade soyle verilebilir F k a b n 1n i 1nH k ki displaystyle F k a b n 1 over n sum i 1 n H k k i Burada H x x0 displaystyle H x x 0 Heaviside tipi bir olup x0 displaystyle x 0 degerde merkezlenen bir bozulmus dagilim icin bir yigmali dagilim fonksiyonudur Bu ifadeyi elde etmek icin gecis noktalarinin hesaplanmasinda tutarli usuller kullanildigi kabul edilmektedir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State