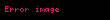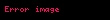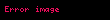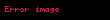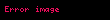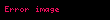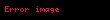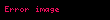Sinüs teoremi, bir çembersel üçgende (kirişler üçgeni) bir kenar ve bu kenar karşısındaki açının sinüsleri oranı sabittir. Sinüs, dik açılı üçgenlerde dik olmayan bir açının karşısında kalan dik kenar ile hipotenüsün (dik açının karşısında kalan kenar) birbirine oranıdır.

, ve üçgenin kenar uzunlukları; , ve üçgenin iç açıları ve çevrel çemberin yarıçapı ise bunlar arasında sinüs teoremine göre aşağıdaki bağıntı mevcuttur:
İspatı

- ABC üçgeninin çevrel çemberinin merkezi
ve yarıçapı
olsun.
ve
yarıçapları çizildiğinde aynı yayı gören çevre ve merkez açılardan dolayı
olur.
merkezinden
kenarına
noktasında yükseklik inildiğinde
ikizkenar üçgen olduğundan yükseklik hem kenarortay hem de açıortay olur. O zaman
üçgeni bir açısı
derece olan dik üçgen olur.
uzunluğu ise
'dir.
- Sinüsün tanımı gereği,
Bu işlem düzenlendiğinde
bulunur.
Aynı işlem diğer kenarlar için de yapıldığında sinüs teoremi bulunmuş olur.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Sinus teoremi bir cembersel ucgende kirisler ucgeni bir kenar ve bu kenar karsisindaki acinin sinusleri orani sabittir Sinus dik acili ucgenlerde dik olmayan bir acinin karsisinda kalan dik kenar ile hipotenusun dik acinin karsisinda kalan kenar birbirine oranidir Sinus teoremi a displaystyle a b displaystyle b ve c displaystyle c ucgenin kenar uzunluklari A displaystyle A B displaystyle B ve C displaystyle C ucgenin ic acilari ve r displaystyle r cevrel cemberin yaricapi ise bunlar arasinda sinus teoremine gore asagidaki baginti mevcuttur asin A bsin B csin C 2r displaystyle a over sin A b over sin B c over sin C 2r IspatiSinus Teoremi ispatinda kullanilan sekilABC ucgeninin cevrel cemberinin merkezi O displaystyle O ve yaricapi r displaystyle r olsun BO displaystyle BO ve OC displaystyle OC yaricaplari cizildiginde ayni yayi goren cevre ve merkez acilardan dolayi m BOC 2m A displaystyle m BOC 2m A olur O displaystyle O merkezinden a displaystyle a kenarina H displaystyle H noktasinda yukseklik inildiginde BOC displaystyle BOC ikizkenar ucgen oldugundan yukseklik hem kenarortay hem de aciortay olur O zaman BOH displaystyle BOH ucgeni bir acisi m BOH A displaystyle m BOH A derece olan dik ucgen olur BH displaystyle BH uzunlugu ise a 2 displaystyle a 2 dir Sinusun tanimi geregi sin BOH sin A a 2r displaystyle sin BOH sin A frac a 2 r Bu islem duzenlendiginde asin A 2r displaystyle a over sin A 2r bulunur Ayni islem diger kenarlar icin de yapildiginda sinus teoremi bulunmus olur
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State