Simpleks algoritması, doğrusal programlama problemlerinde optimum çözümü pratik olarak bulmak amacıyla George Dantzig tarafından 1947 yılında geliştirilen bir algoritmadır.

Bu algoritma kısıtlamalardan ortaya çıkan düzeyleri birçok değişirli polihedron (iki değişkenli problemde "uygunluk alanı") olarak görmekte ve bu polihedronda kesişme noktalarını yani polihedron köşelerini (iki değişkenli problemde kısıtlama çizgilerinin kesişme noktalarını) birer mümkün çözüm olarak görmektedir. Bundan sonra bir köşeden başlayıp bu köşeyi tayin eden kenarlar takip edilerek amaç fonksiyonun iyileşmesini sağlayan kenarlar teşhis edilmekte; bunlardan amaç fonksiyonuna en iyi sonuç çıkaracak kenar takip edilip bir diğer polihedron köşesi bulunmaktadır. Bu yeni bulunan polihedron köşesi de aynı yöntem kullanılarak daha iyi bir başka köşeye gidebilme imkânı aranmaktadır. Eğer elde bulunan bir polihedron köşesinden daha iyi amaç sonuç sağlayan bir köşeye gitme imkânı yoksa, bu son köşe optimum çözum olarak kabul edilmektedir.
Genel aktarım
Doğrusal programlamada simpleks algoritması aşağıda gösterilen standart formda uygulanır:
- En yüksek büyüklüğe çıkar
- Aşağıdaki koşullar altında
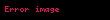
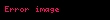
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Simpleks algoritmasi dogrusal programlama problemlerinde optimum cozumu pratik olarak bulmak amaciyla George Dantzig tarafindan 1947 yilinda gelistirilen bir algoritmadir Karsilik gelen lp yi cozmek icin simpleks yontemiyle alinan olasi bir yolla kirmizi birlikte dogrusal bir programlama politopunu gosterir Bu algoritma kisitlamalardan ortaya cikan duzeyleri bircok degisirli polihedron iki degiskenli problemde uygunluk alani olarak gormekte ve bu polihedronda kesisme noktalarini yani polihedron koselerini iki degiskenli problemde kisitlama cizgilerinin kesisme noktalarini birer mumkun cozum olarak gormektedir Bundan sonra bir koseden baslayip bu koseyi tayin eden kenarlar takip edilerek amac fonksiyonun iyilesmesini saglayan kenarlar teshis edilmekte bunlardan amac fonksiyonuna en iyi sonuc cikaracak kenar takip edilip bir diger polihedron kosesi bulunmaktadir Bu yeni bulunan polihedron kosesi de ayni yontem kullanilarak daha iyi bir baska koseye gidebilme imkani aranmaktadir Eger elde bulunan bir polihedron kosesinden daha iyi amac sonuc saglayan bir koseye gitme imkani yoksa bu son kose optimum cozum olarak kabul edilmektedir Genel aktarimDogrusal programlamada simpleks algoritmasi asagida gosterilen standart formda uygulanir En yuksek buyukluge cikarcT x displaystyle mathbf c T cdot mathbf x dd Asagidaki kosullar altindaAx b xi 0 displaystyle mathbf A mathbf x leq mathbf b x i geq 0 dd x x1 xn displaystyle x x 1 dots x n problemin degiskenleri c c1 cn displaystyle c c 1 dots c n amac fonksiyonunun sabitleri A bir p n matrisi ve b b1 bp displaystyle b b 1 dots b p bj 0 displaystyle b j geq 0 kosulu ile sabitler Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State