Bu madde olması gerekenden az içermektedir veya içermemektedir. (Mayıs 2017) |
Bu madde, uygun değildir. (Mayıs 2011) |
Ramsey Kuramı, 20. yüzyılın ilk yarısında yaşamış olan İngiliz matematikçi ve filozof Frank Ramsey, adını taşıyan ve "bir yapıda belirlenmiş bir özelliğin var olması için en az kaç eleman kullanılması yeterlidir" sorusunu temel alan bir teori. Ramsey kuramının sorularından biri; bir odadaki sonsuz tane insanın ya hepsinin birbirini tanıması ya da hiçbirinin birbirini tanımamasıdır.
Ramsey teoremi
n sayıda renk ve sonsuz sayıda noktamız olsun. Her iki nokta, bu n renkten birine boyanmış bir kenarla birleştirilmiş olsun. O zaman, bütün noktaları aynı renk kenarla birleştirilmiş sonsuz tane noktadan oluşan bir küme vardır.
Her insan bir nokta olarak gösterilsin. Eğer iki insan birbirini tanıyorsa, bu iki insanı birbirine kırmızı bir çizgiyle bağlayalım. Eğer iki insan birbirini tanımıyorsa, bu iki insanı da mavi bir çizgiyle bağlayalım. Her ikisi kırmızı ya da mavi çizgiyle birleştirilmiş sonsuz tane nokta elde edilir. Bu noktalar arasından, hep aynı renkle (ya hep kırmızıyla ya hep maviyle) birleştirilmiş sonsuz tane nokta bulunabilir.
Kanıt
Kanıt, iki aşamada gerçekleşir. Birinci aşamada, sonsuz tane 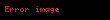
















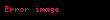
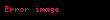



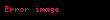

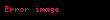

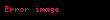
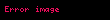
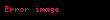
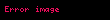

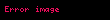
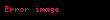
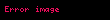


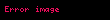
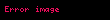
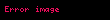
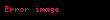
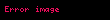

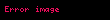
















Kanıtın birinci aşaması tamamlandı. İkinci aşama:
Seçilen 






Sonsuz sayıda nokta olduğundan ve yalnızca iki renk olduğundan, 










Ramsey sayıları
Teorem: a ve b herhangi iki doğal sayı olsun. Öyle bir N vardır ki, eğer n ≥ N ise, kenarları A ve B renklerine boyanmış 


Tanım: Eğer bir çizgenin bütün köşe noktaları birbiri ile yalnız ve ancak bir bağ yapıyorsa bunlara tam çizgeler denir ve köşe noktası sayısına göre adlandırılır. Örneğin 


Teoremde en küçük N sayısına Ramsey sayısı denir ve r(a, b) olarak yazılır.
Yukarıdaki örnek r(3,3)=6 olur.
Bazı r(a, b) sayılarını bulmak kolay ; r(1, b)=1 r(2, b)=b Ramsey sayıları için genel bir formül bilinmiyor. Ramsey sayılarının bulunması çizge kuramının sorularından biridir.
Paul Erdős ve ’in teoremi r(a, b) sayılarına üst sınır getiriyor.
Teorem: a≥2 ve b≥2 iki tam sayıysa, r(a, b) ≤ r(a, b-1)+r(a-1, b-a*1) Eğer r(a, b-1) ve r(a-1, b) sayılarının ikisi de çiftse r(a, b) < r(a, b-1)+r(a-1, b).
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde olmasi gerekenden az ic baglanti icermektedir veya hic icermemektedir Lutfen bu sayfadan ilgili maddelere ic baglanti vermeye calisin Mayis 2017 Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Mayis 2011 Ramsey Kurami 20 yuzyilin ilk yarisinda yasamis olan Ingiliz matematikci ve filozof Frank Ramsey adini tasiyan ve bir yapida belirlenmis bir ozelligin var olmasi icin en az kac eleman kullanilmasi yeterlidir sorusunu temel alan bir teori Ramsey kuraminin sorularindan biri bir odadaki sonsuz tane insanin ya hepsinin birbirini tanimasi ya da hicbirinin birbirini tanimamasidir Ramsey teoremin sayida renk ve sonsuz sayida noktamiz olsun Her iki nokta bu n renkten birine boyanmis bir kenarla birlestirilmis olsun O zaman butun noktalari ayni renk kenarla birlestirilmis sonsuz tane noktadan olusan bir kume vardir Her insan bir nokta olarak gosterilsin Eger iki insan birbirini taniyorsa bu iki insani birbirine kirmizi bir cizgiyle baglayalim Eger iki insan birbirini tanimiyorsa bu iki insani da mavi bir cizgiyle baglayalim Her ikisi kirmizi ya da mavi cizgiyle birlestirilmis sonsuz tane nokta elde edilir Bu noktalar arasindan hep ayni renkle ya hep kirmiziyla ya hep maviyle birlestirilmis sonsuz tane nokta bulunabilir KanitKanit iki asamada gerceklesir Birinci asamada sonsuz tane a0 a1 a2 ai ai 1 aj 2 displaystyle a 0 a 1 a 2 a i a i 1 a j 2 noktasi alinir her ai displaystyle a i kendisinden sonra gelen ai 1 ai 2 ai 3 displaystyle a i 1 a i 2 a i 3 noktalariyla ayni renk cizgiyle ya hep kirmizi ya hep mavi cizgiyle baglanmistir a0 displaystyle a 0 herhangi bir nokta olsun a1 a2 a3 displaystyle a 1 a 2 a 3 noktalari oyle secilmeli ki a0 displaystyle a 0 noktasi bu noktalarla hep ayni renk cizgiyle baglanmis olsun a0 displaystyle a 0 noktasi kisileri simgeleyen obur noktalarla ya kirmizi ya da mavi bir cizgiyle baglanmistir Sonsuz tane nokta oldugundan ve yalnizca iki tane baglanti rengi oldugundan a0 displaystyle a 0 in ayni renk cizgiyle baglandigi sonsuz tane nokta vardir a0 displaystyle a 0 in hep ayni renk cizgiyle baglandigi sonsuz bir nokta kumesi alalim Bu kumeye A0 displaystyle A 0 diyelim Demek ki a0 displaystyle a 0 A0 displaystyle A 0 in noktalariyla hep ayni renk cizgiyle baglanmistir a0 displaystyle a 0 noktasindan sonraki a1 a2 a3 displaystyle a 1 a 2 a 3 noktalarini A0 displaystyle A 0 kumesinden secelim Boylece a0 displaystyle a 0 noktasi istenen kosulu saglar A0 displaystyle A 0 dan herhangi bir a1 displaystyle a 1 noktasi alalim a1 displaystyle a 1 noktasi A0 displaystyle A 0 in obur noktalarina ya kirmizi ya da mavi bir renkle baglanmistir A0 displaystyle A 0 da sonsuz tane nokta oldugundan ve yalnizca iki rengimiz oldugundan A0 displaystyle A 0 kumesinde a1 displaystyle a 1 in ayni renk cizgiyle baglandigi sonsuz tane nokta vardir Yani ya a A0 displaystyle A 0 a1 displaystyle a 1 noktasi a yla kirmizi bir cizgiyle baglanmis kumesi ya da a A0 displaystyle A 0 a1 displaystyle a 1 noktasi a yla mavi bir cizgiyle baglanmis kumesi sonsuzdur Bu kumelerden sonsuz olanina A1 displaystyle A 1 diyelim Demek ki a1 displaystyle a 1 A1 displaystyle A 1 in noktalariyla hep ayni renk cizgiyle baglanmistir a2 a3 a4 displaystyle a 2 a 3 a 4 noktalari da A1 displaystyle A 1 kumesinden secilir ve boylece yukaridaki kosul a1 displaystyle a 1 icin saglanmis olur A1 displaystyle A 1 den herhangi bir a2 displaystyle a 2 noktasi alalim a2 displaystyle a 2 noktasi A1 displaystyle A 1 in obur noktalariyla ya kirmizi ya da mavi bir cizgiyle baglanmistir A1 displaystyle A 1 de sonsuz nokta oldugundan ve yalnizca iki rengimiz oldugundan A1 displaystyle A 1 de a1 displaystyle a 1 in hep ayni renkle baglandigi sonsuz tane nokta vardir Bir baska deyisle ya a A1 displaystyle A 1 a2 displaystyle a 2 noktasi a yla kirmizi bir cizgiyle baglanmis kumesi ya da a A1 displaystyle A 1 a2 displaystyle a 2 noktasi a yla mavi bir cizgiyle baglanmis kumesi sonsuzdur Bu kumelerden sonsuz olanina A2 displaystyle A 2 diyelim Demek ki a2 displaystyle a 2 A2 displaystyle A 2 nin noktalariyla hep ayni renk cizgiyle baglanmistir a3 a4 a5 displaystyle a 3 a 4 a 5 noktalarini A2 displaystyle A 2 de secilir ve boylece yukaridaki kosul a2 displaystyle a 2 icin saglanmis olur A2 displaystyle A 2 den herhangi bir a3 displaystyle a 3 noktasi alalim Yukarida yapilanlari a3 displaystyle a 3 ve A2 displaystyle A 2 icin yapalim A2 displaystyle A 2 nin icinde oyle bir sonsuz A3 displaystyle A 3 kumesi bulalim ki a3 displaystyle a 3 A3 displaystyle A 3 un her noktasiyla hep ayni renk cizgiyle baglanmis olsun Bunu boylece sonsuza kadar surdurebiliriz Demek ki oyle a0 a1 a2 a3 a4 ai ai 1 ai 2 displaystyle a 0 a 1 a 2 a 3 a 4 a i a i 1 a i 2 noktalari bulunur ki her nokta kendisinden sonra gelen noktalarla ayni renk cizgiyle baglanmis olur Kanitin birinci asamasi tamamlandi Ikinci asama Secilen a0 a1 a2 a3 displaystyle a 0 a 1 a 2 a 3 noktalarinin her birine bir renk verilir Eger bir nokta kendisinden sonra gelen noktalarla hep kirmizi cizgiyle baglanmissa o noktaya kirmizi nokta diyelim Yoksa o noktaya mavi nokta diyelim Ornegin eger a0 displaystyle a 0 noktasi kendisinden sonra gelen a1 a2 a3 displaystyle a 1 a 2 a 3 noktalariyla hep kirmizi bir cizgiyle baglanmissa a0 displaystyle a 0 noktasi kirmizi noktadir Eger a5 displaystyle a 5 noktasi kendisinden sonra gelen a6 a7 a8 displaystyle a 6 a 7 a 8 noktalariyla hep mavi cizgiyle baglanmissa a5 displaystyle a 5 noktasi mavi noktadir Sonsuz sayida nokta oldugundan ve yalnizca iki renk oldugundan a0 a1 a2 a3 displaystyle a 0 a 1 a 2 a 3 noktalarindan sonsuz tanesi ayni renk noktadir Bir baska deyisle ya kirmizi noktalar kumesi ya da mavi noktalar kumesi sonsuzdur Matematiksel olarak ya ai displaystyle a i ai displaystyle a i kirmizi bir nokta ya da ai displaystyle a i ai displaystyle a i mavi bir nokta kumesi sonsuzdur Iki kume birden de sonsuz olabilir ama en azindan birinin sonsuz oldugunu biliyoruz Iki kumeden sonsuz olanini alalim Obur noktalari atalim Noktalari yeniden adlandirarak her noktanin ayni renk oldugunu varsayalim hepsi kirmizi olsun Demek ki a0 a1 a2 a3 a4 displaystyle a 0 a 1 a 2 a 3 a 4 noktalarinin her birinin kirmizi oldugunu varsaydik Bu kumeden iki nokta alalim ai displaystyle a i ve aj displaystyle a j i j den daha kucuk ai displaystyle a i kirmizi bir nokta olsun ai displaystyle a i noktasi aj displaystyle a j noktasiyla kirmizi bir cizgiyle baglanir Demek ki yukaridaki sonsuz nokta birbirleriyle ayni renk cizgiyle kirmiziyla baglanmistir Ramsey in teoremi kanitlanmis oldu Ramsey sayilariTeorem a ve b herhangi iki dogal sayi olsun Oyle bir N vardir ki eger n N ise kenarlari A ve B renklerine boyanmis Kn displaystyle K n tam cizgesinde ya tamamen A renkli bir Ka displaystyle K a ya da tamamen B renkli bir Kb displaystyle K b vardir Tanim Eger bir cizgenin butun kose noktalari birbiri ile yalniz ve ancak bir bag yapiyorsa bunlara tam cizgeler denir ve kose noktasi sayisina gore adlandirilir Ornegin Kn displaystyle K n n kosesi olan tam cizgenin gosterimi icin kullanilir K3 displaystyle K 3 cizgesi bir ucgen belirtir Tanima gore 6 kenarli ve iki renkli bir duzenli tam cizge cizilirse iki renkten birinde mutlaka bir K3 displaystyle K 3 bulunur Teoremde en kucuk N sayisina Ramsey sayisi denir ve r a b olarak yazilir Yukaridaki ornek r 3 3 6 olur Bazi r a b sayilarini bulmak kolay r 1 b 1 r 2 b b Ramsey sayilari icin genel bir formul bilinmiyor Ramsey sayilarinin bulunmasi cizge kuraminin sorularindan biridir Paul Erdos ve in teoremi r a b sayilarina ust sinir getiriyor Teorem a 2 ve b 2 iki tam sayiysa r a b r a b 1 r a 1 b a 1 Eger r a b 1 ve r a 1 b sayilarinin ikisi de ciftse r a b lt r a b 1 r a 1 b
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State